Bonsoir,
je reprends un ancien projet qui consiste à calculer numériquement la trajectoire d'un rayon lumineux dans la métrique de Friedmann-Lemaitre avec le cas "k=0" et la constante cosmologique nulle. Le rayon est émis par une galaxie source à l'instant t0 (aujourd'hui) et à une distance prise en paramètre (que je pense devoir noteravec R0 le facteur d'échelle d'aujourd'hui et r0 la coordonnée radiale aussi d'aujourd'hui.
D'après l'équation des géodésiques, j'obtiens l'équation suivante :
représente donc le facteur d'échelle d'aujourd'hui (temps correspondant à l'émission du rayon).
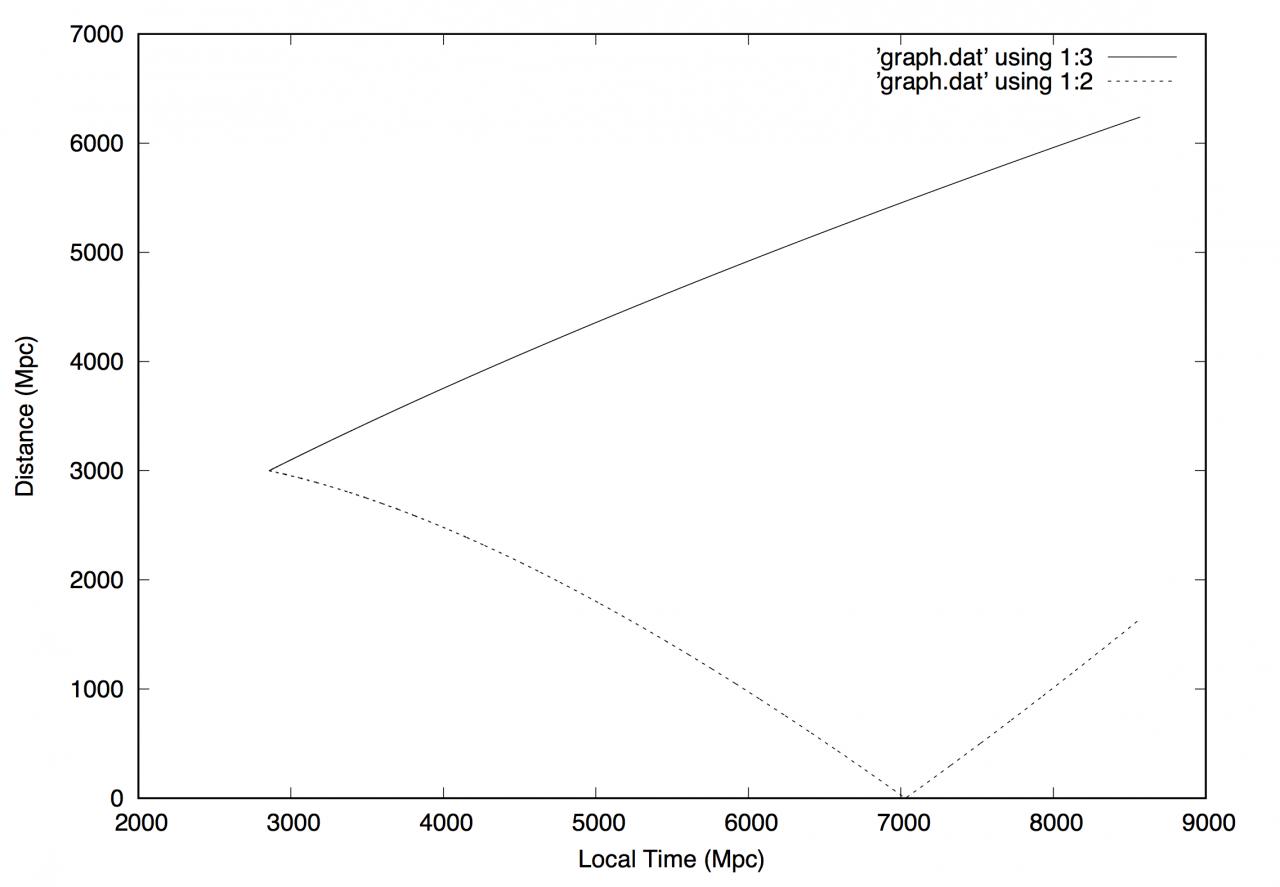
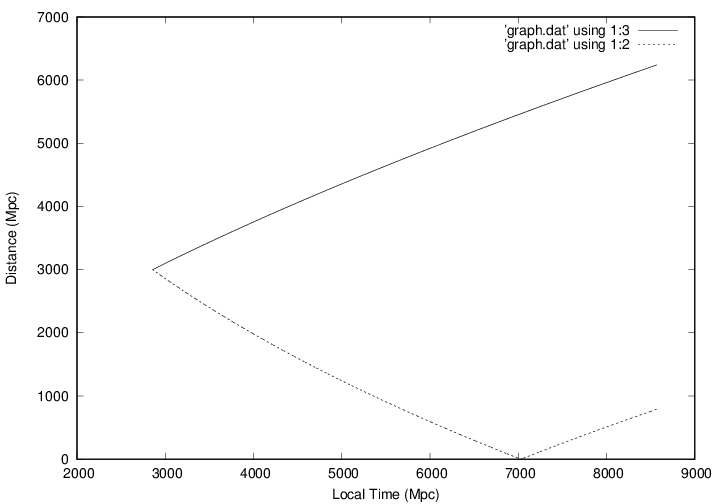
Dans mon code, j'ai pris, par commodité mais du coup, je me demande si les résultats sur la figure ci-dessous sont bons.
Voici la figure représentant ces résultats : la courbe (en ligne continue) en haut représente la trajectoire de la galaxie source et l'axe "Ox" du bas notre galaxie (je représente en fait le temps local en unité de MegaParsec). La distance initiale choisie ici est 3000 Mpc.
La ligne en pointillé représente la trajectoire du rayon lumineux (qui arrive dans notre galaxie vers 7000 MegaParsec en temps local). Ne tenez pas compte du rebond après l'arrivée, c'est juste que j'ai imposé une valeur positive pour la coordonnée radiale "r" du rayon lumineux.
Ce que je voudrais savoir, c'est si je dois multiplier ou non chaque valeur numérique de la coordonnée radiale (autrement dit) par le facteur d'échelle
avec
le temps courant , ceci pour représenter la distance physique par rapport à nous.
Dans la figure ci-dessus, je n'ai pas multiplié la coordonnée radialepar
.
Si quelqu'un pouvait m'expliquer si je dois appliquer ou non ce facteur, ça serait sympa.
-----





 )
)