Géodésiques lumière et autres trajectoires
Discussions similaires
-
Par invite231234 dans le forum Physique
Réponses: 20
Dernier message: 29/01/2012, 15h08
-
Par invite46ee2a36 dans le forum TPE / TIPE et autres travaux
Réponses: 0
Dernier message: 24/11/2005, 09h03
-
Par invitec0a5a65e dans le forum Astronautique
Réponses: 4
Dernier message: 16/11/2004, 12h33
-
Par invite3e313b9b dans le forum Physique
Réponses: 13
Dernier message: 25/11/2003, 16h10
-
Par invite3e313b9b dans le forum Physique
Réponses: 0
Dernier message: 07/11/2003, 14h47









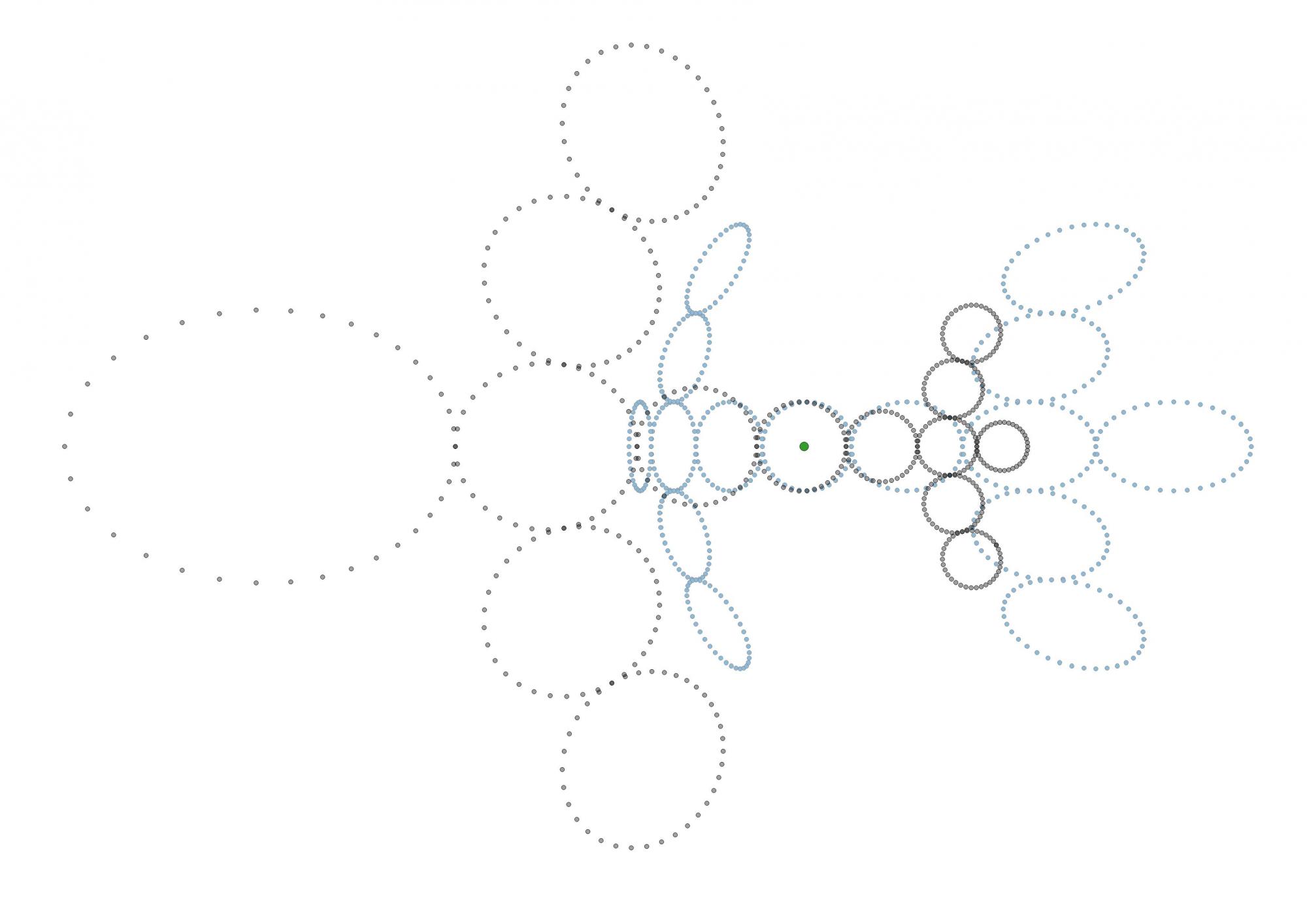

 Il semblerait qu'il y ai un point de convergence au niveau du centre de l'ovoïde (bleu) située la plus en avant
Il semblerait qu'il y ai un point de convergence au niveau du centre de l'ovoïde (bleu) située la plus en avant