matrice de passage : quelle est la version officielle entre ces 2 ?

[invite9c7554e3]

Bonjour tous,

j'ouvre une discussion sur les matrices de passage car je trouve 2 versions différentes sur le net et j'aimerais comprendre pourquoi. Attention cette discussion ne porte pas sur les matrices de rotation utilisées pour les transformation de vecteur de base puisque j'ai déjà ouvert une discussion ici http://forums.futura-sciences.com/ma...-resultat.html


Definition:
une matrice de passage (de la base B vers B') contient en colonne les coordonnées des vecteurs de la base B' en fonction des coordonnées de la base B. Pour une rotation dans le plan on a donc la

1ere version :
Sur ces liens :
https://tice.agroparistech.fr/course...cidReq=RAPMATH
http://uel.unisciel.fr/physique/outi...e_ch11_19.html

les auteurs définissent le changement de base comme l'opération

et ceci est bien documenté sur wikipedia UK où on a une démonstration https://en.wikipedia.org/wiki/Rotation_of_axes :
Sans nom 2.jpg

j'en déduis donc que la relation de changement de base d'une matrice est :

car on a : , , ,
donc et en multipliant par on a :

2eme version :
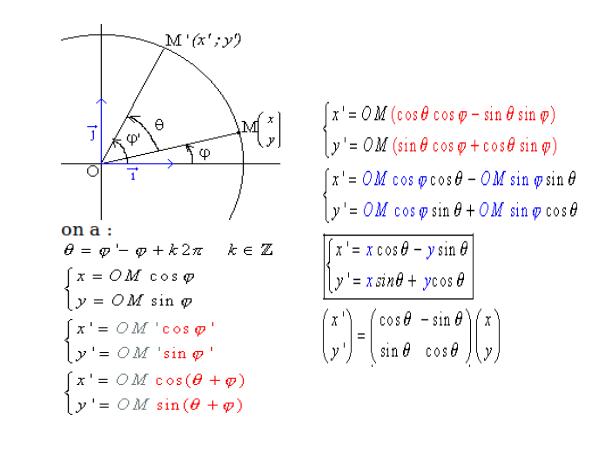
La démonstration ci-dessous nous donne la relation qui permet de passer des anciennes coordonnées aux nouvelles en accord avec ce lien : http://homeomath2.imingo.net/rotation.htm :
On a avec cette démonstration :
Sans nom 1.jpg
et j'en déduis donc que :

Conclusion:
j'ai une même matrice de passage définit comme la matrice permettant de passer de la base B à la base B' et j'ai deux relations différente :
ou
avec deux démonstrations où je ne trouve pas d'erreur ?

Pourriez vous me dire svp qu'elle est la bonne version où plutôt celle classiquement utilisée ? Pourriez vous m'expliquez quelle est la différence entre les deux démonstrations pour que l'on ne trouve pas le même résultat ?
merci beaucoup
-----

[invite9c7554e3]

en gros ma question est :

faites vous :


ou :


et pourquoi ?

(avec P la matrice de passage de B vers B', où on met en colonne les vecteurs unitaires de B' exprimé dans B)

[invite23cdddab]

avec P la matrice de passage de B vers B', où on met en colonne les vecteurs unitaires de B' exprimé dans B

Ça c'est la matrice de passage de B' vers B.

Si le premier vecteur de la base a pour coordonnées dans la base B , alors la matrice P de passage de B vers B' doit vérifier , vu que le vecteurs de coordonnées (a,b,c) a comme coordonnées (1,0,0) dans la nouvelle base

La matrice de passage de B vers B' a pour colonnes les vecteurs unitaires de B exprimés dans B'

[Amanuensis]

(avec P la matrice (...) où on met en colonne les vecteurs unitaires de B' exprimé dans B)

On a alors les coordonnés du premier vecteur unitaire de B' exprimé dans B, etc.

Donc c'est



(Réponse compatible avec la précédente.)

[A voir en vidéo sur Futura]

[invite9dc7b526]

les auteurs définissent le changement de base comme l'opération

bonjour,

il faut faire attention à ne pas confondre application linéaire (opération dans le jargon de la phyique?) et matrice. La matrice de passage est souvent définie comme la matrice de l'application identité dans les bases b' et b. Tu peux toujours désigner par P la matrice et l'application mais dans la relation X=PX' si P est l'identité alors X'=X (écrit avec d'autres coordonnées). Il n'y a pas de réelle difficulté mais il faut en être conscient.

[invite9c7554e3]

tout d'abord merci tous de prendre le temps de m'aider car je suis vraiment pommé, je confond tout à présent

je réponds si dessous aux première remarques que je ne comprends pas

Ça c'est la matrice de passage de B' vers B. La matrice de passage de B vers B' a pour colonnes les vecteurs unitaires de B exprimés dans B'

ça commence déjà mal car je n'ai pas la même définition
j'ai pris la définition que j'ai trouvé dans un lien sur le net (je ne sais plus où...) mais qui est la même que sur wikipedia :
https://fr.wikipedia.org/wiki/Matrice_de_passage

Du coup je bloque déjà, quelle définition est la bonne ? Les deux conventions existent ?

Si le premier vecteur de la base a pour coordonnées dans la base B , alors la matrice P de passage de B vers B' doit vérifier , vu que le vecteurs de coordonnées (a,b,c) a comme coordonnées (1,0,0) dans la nouvelle base

c'est une bonne idée de faire ça... je vais l'appliquer dans mon cas où je considère que la matrice de wikipedia est la bonne et où je consière que mes vecteurs X' X et ma matrice P sont exprimés dans le repère de départ (i,j):

Si j'en crois le premier lien que j'ai mis dans mon premier message alors mon calcul est correct mais si j'en crois le 2eme calcul alors c'est faux
bref, je capte plus rien moi j'aurais tendance à penser que dans la base de départ "(i,j)" le vecteur de base X' à pour composante (cos,sin) ou je fais une erreur grossière ?

On a alors les coordonnés du premier vecteur unitaire de B' exprimé dans B, etc.
Donc c'est

C'est ce que je viens d'appliquer ci dessus ou je me trompe ?

(Réponse compatible avec la précédente.)

Tu parles de la réponse de Tryss ou de la réponse dans le précédent sujet que j'avais ouvert ?

- Pour moi ta réponse est l'opposé de celle de Tryss car j'ai définis P comme étant la matrice de passage de B vers B' et la relation que tu donnes Tryss semble dire qu'elle est fausse puisque pour lui le P que j'ai définit est de B' vers B

- si tu parles de l'autre sujet sur les rotations alors ce n'est pas cohérent car on a fait des opérations telle que ce qui n'est pas cohérent avec le fait d'avoir

Pour conclure sur cette premiere discussion j'ai l'impression que Tryss a raison mais qu'il utilise une autre conviention que je ne comprends pas

[Amanuensis]

Tu parles de la réponse de Tryss ou de la réponse dans le précédent sujet que j'avais ouvert ?

De la réponse de Tryss.

- Pour moi ta réponse est l'opposé de celle de Tryss

Mais ce n'est pas le cas, et c'est pour cela que j'ai ajouté la phrase sur la compatibilité. Les différences entre les deux réponses sont :

1) J'ai répondu avec les notations de la question

2) Je n'ai rien exprimé sur le terme "matrice de passage".

car j'ai définis P comme étant la matrice de passage de B vers B' et la relation que tu donnes Tryss semble dire qu'elle est fausse puisque pour lui le P que j'ai définit est de B' vers B

Je n'ai pas cherché à prendre un côté ou l'autre pour le terme "matrice de passage". Je ne sais pas quel est l'usage, et pour moi ce n'est qu'un problème de terminologie, de convention.

- si tu parles de l'autre sujet sur les rotations alors ce n'est pas cohérent car on a fait des opérations telle que ce qui n'est pas cohérent avec le fait d'avoir

Je ne dis pas le contraire. Sans connaissance a priori des usages, je penche "naturellement" vers X' = PX, et c'est comme cela que j'ai répondu dans l'autre fil, en précisant ce que j'utilisais. Cela ne donne aucune information sur les "usages".

-------

En résumé, ne pas prendre mes interventions comme portant sur le débat de terminologie ou des usages.

[invite23cdddab]

Tout à coup tu me met le doute, il me parait raisonnable que la matrice de passage de la base B vers la base B' prends un vecteur exprimé dans la base B et l'exprime dans la base B' (on passe de B à B'), mais il est possible que je me plante

[Amanuensis]

car je suis vraiment pommé, je confond tout à présent

Dans ces cas là, il me semble qu'il faut revenir aux faits indépendamment de la terminologie. Et admettre que la terminologie n'est pas normalisée, qu'il peut y avoir plusieurs conventions, et donc s'adapter aux auteurs, au contexte.

Clairement il y a deux matrices de passages, l'une étant l'inverse de l'autre. Laquelle est laquelle pourrait être conventionnel.

Perso, j'ai aussi fortement en tête "dans quoi vit chaque notion", pour paraphraser MiPaMa. Et ici cela amène à distinguer les vecteurs qui vivent dans l'espace vectoriel d'un côté (notons le M), et leurs composantes de l'autre, qui vivent dans R^3. Pour moi un vecteur n'est pas un "triplet de réels". De même cela amène à distinguer les rotations et leurs matrices.

En termes mathématiques, cela revient à voir une "base" comme une application bijective entre M et R^3. Notons B et B' ces applications dans le sens M -> R^3

Vu comme cela une matrice de passage est une application linéaire interne à R^3, soit B o B'^{-1}, soit B' o B^{-1}. Et si on les écrit comme cela, il y a moins d'ambiguïté. (En particulier je ne vois de matrice que comme une représentation d'une application linéaire interne à R^3, pas comme représentant d'une application linéaire interne à M.)

En reconstruisant cela dans ma tête, je ne me sens pas paumé.

[invite9c7554e3]

En fait je m'en fou pas mal aussi des conventions tant que c'est "physiquement correct" le soucis et que je suis tellement pommé à présent que je ne sais plus ce qui est cohérent ou pas.

Par exemple j'ai trouvé et je ne sais même plus dire si c'est juste ou pas tellement mon cerveau est embrouillé

Dans mon premier message on a deux relations différente qui sont données à partir de 2 démonstration:
X'=P.X
et
X=P.X'

et je me dis que puisque P est définit de la même façon alors il y en a une des deux qui n'est pas correcte.

[invite9c7554e3]

En fait je n'avais pas remarqué que les x' et y' de mon premier message ne sont pas définis de la même façon dans la 1ere et 2sd source

Pour bien différentier les 2 je vais utiliser la lettre R pour la transformation de le base et Q pour la matrice de transformation des coordonnées. Avec, bien entendu

Ce qui perturbe maintenant c'est plus de la terminologie (je crois), notamment qu'es ce que l'on appelle matrice de passage en math, es ce Q ou R ?

- la matrice qui permet de transformer les axes de la base R ?

- la matrice qui permet de transformer les coordonnées Q ? (je crois que c'est ça)

Vérification de ce que je crois être correct, pouvez vous me confirmer svp (?) :

1) Pour une "rotation de la base" (ce qui correspond au cas n°1 énoncé + haut ?) on a :





2) Pour une "rotation des coordonnées" (ce qui correspond au cas n°2 énoncé + haut ?) on a :


3) Définition mathématique
je lis dans un cours de math que la matrice de passage de B vers B' est construite en mettant en colonne les coord. de la nouvelle base exprimmées dans l'ancienne base. on a donc la matrice de passage qui est définie en math comme la matrice P telle que :


J'en déduis donc que P=Q es ce correct ?

Ce qui m'a perturbé et pourquoi j'ai écris le message :

Je vois que P=Q et je me dis donc que la relation de transformation qui doit être utilisée en math est :



Mais là... perdu : en math on me dit que l'on transforme un vecteur X en un vecteur X' par la relation



Ma conclusion :
en math lorsqu'on utilise X et X' ne sont pas des vecteurs contenant des coordonnées mais des vecteurs contenant les vecteurs de base comme dans le cas 1)

Si non alors comment peut on dire que la relation 2) est correcte et à la fois dire que est correcte également ?

[invite9c7554e3]

la seule façon pour que tout soit cohérent pour moi c'est qu'une matrice de passage soit définie tel que :


on met en colonne les composantes de l'ancienne base dans la nouvelle base

Alors là je serai d'accord pour dire que :


et je serai d'accord avec le changement de base :



Mais je n'ai pas l'impression que ceci soit la définition standard d'une matrice de passage contrairement au message de Tryss

[invite9dc7b526]

je le répète, tu confonds matrice de passage (qui est la matrice de l'identité dans deux bases) et matrice d'une rotation (qui est la matrice d'une certaine application dans une certaine base). Les deux peuvent avoir les mêmes composantes mais leur usage n'est pas le même. Que signifie par exemple le produit PX où P est une matrice de passage et X un vecteur?

[invite9c7554e3]

merci minushabens,
je n'ai effectivement pas compris ta remarque. Pour moi P.X représente l'opération de transformation du vecteur X en un vecteur X'

[invite9c7554e3]

je viens de vérifier dans un cours de math :
http://www.math.univ-toulouse.fr/~ha...sDePassage.pdf

La matrice de passage est définie comme étant la matrice qui à en colonne les composantes des vecteurs de la nouvelle base B' exprimés dans l'ancienne base B.

Donc, si on applique ceci à une rotation dans le plan, la matrice de passage de B à B' s'exprime ainsi :


Ceci correspond à la matrice que j'ai noté Q

Donc ce qui me semble correct c'est d'écrire :


Mon soucis est que sur internet je trouve la même définition pour P mais pas la même transformation :
http://uel.unisciel.fr/physique/outi...e_ch11_19.html

[invite9c7554e3]

désolé je voulais écrire:

[invite51d17075]

- la matrice qui permet de transformer les axes de la base R ?

- la matrice qui permet de transformer les coordonnées Q ? (je crois que c'est ça)

il me semble que même si tu reconnais une diff entre les deux , tu es à chaque fois un peu mélangé dans tes calculs en passant de l'une à l'autre.
cordialement

[invite9dc7b526]

Il y a certainement plusieurs façons de voir les choses, mais je les présenterais ainsi: on a un espace vectoriel de dimension n et deux bases e=(e1,..,en) et f=(f1,..,fn). La matrice de passage est la matrice P dont les colonnes sont les coordonnées des fi dans la base e. Ca signifie que fi=p1i*e1+..+pni*en pour tout i <je mets une étoile pour le produit>

Maintenant, on considère un vecteur u qui s'écrit a1*e1+..an*en = a'1*f1+...+a'n*fn. En d'autres termes X=(a1,..,an) est la liste des cordonnées de u dans la base e et X'=(a'1,..;a'n) la liste des coordonnées de u dans la base f.

on écrit u=a'1*f1+..+a'n*fn = a'1*(p11*e1+...+pn1*en)+...+a' n*(pn1*e1+...+pnn*en) = (a'1*p11+...+a'n*p1n)*e1+...+( a'1*pn1+...+a'n*pnn)*en

et donc on a bien X=PX'

[invite9c7554e3]

Merci tous pour votre aide, je vais eclaircir un peu mon propos :
-----------------------------

Les notations que j'utilise ici sont :

- P est la matrice de passage telle que définie en math (en place en colonne les composantes des vecteurs de base de B' exprimées dans B)

- R est une matrice de rotation (transposée de Q) qui permet de transformer les vecteurs de base selon la fomule :



- Q est la matrice de rotation qui me permet de transformer les coordonées X en X' en accord avec le schéma ci dessous. Est on déjà d'accord pour écrire, sur base de ce schéma que ?




Je reprend le raisonnement mais en sens inverse :

1- Je pars du principe que avec X qui représente les coordonnées dans B et X' celles dans B'

2- j'observe avec le schéma que je viens de rappeler dans ce message (juste au dessus) que l'on a la relation suivante qui doit etre vérifiée:



3- Puisqu'on a et j'en déduis que , est on d'accord jusqu'ici ? (si non je calcul de ce schéma est faux?)

4- maintenant, j'en ai déduis que juste en transposant la matrice Q donnée par le schéma ci-dessus

5-Lorsque je regarde cette matrice P je ne trouve pas ça cohérent avec la définition d'une matrice de passage telle que définie classiquement en math puisque j'ai la transposée.

6- ce que j'en déduis :

- ce que vous appellez X' ou X ce n'est pas un vecteur contenant les coordonnées d'un point mais un vecteur comportant les vecteurs de base ?

- sinon la démonstration que j'ai mis dans l'image ci dessus est fausse ?