Bonjour,
Le schéma proposé représente un observateur qui fait un tour complet sur lui même dans le temps que met la lumière d'une source lointaine à lui parvenir. La rotation est découpée en 10 intervales réguliers. Du point de vue de l'observateur la lumière va en ligne droite. La spirale représente le chemin que doit réellement parcourir la lumière dans le référentiel tournant de l'observateur. Plus l'objet est distant plus l'énergie du photon va étre étallée.
Ce dessin a-t-il un sens ?
Je me doute que les effets Coriolis et Sagnac doivent intervenir, mais y aurait-il une façon simple d'expliquer ceci ?
La rotation d'un objet induit-il un redshift de sa perception, notre propre rotation (terre, galaxie) joue-t-elle un role dans notre perception de l'univers ?
Merci d'avance pour votre aide
Mailou
-----



 )
) 


 )
) je construis un pont droit dans un référentiel fixe (si ça veut dire qq chose...)
je construis un pont droit dans un référentiel fixe (si ça veut dire qq chose...)

 où
où 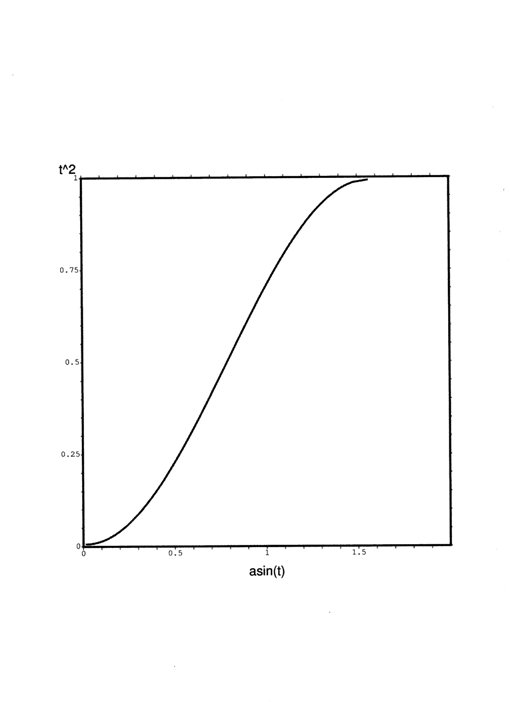


 ) variable et suppérieure à C
) variable et suppérieure à C 