[Géométrie de l'espace] - Cube

[pyrosman]

Bonjour,

Voici mon problème. Je bloque sur un exercice de géométrie de l'espace. On vient de finir le chapitre géométrie vectoriel avec les produits scalaires.

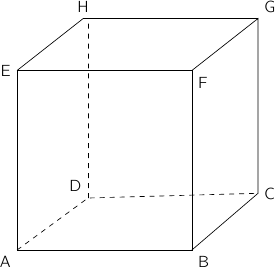
L'exercice est le suivant. On a le cube ci-dessous (voir image) et je dois trouver les angles suivant :
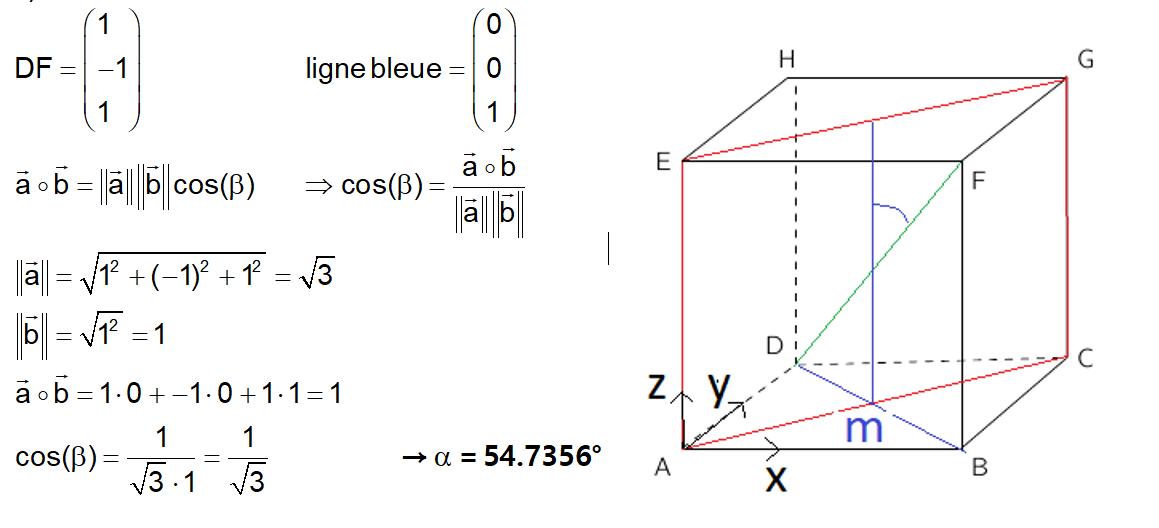
1) entre la diagonale du cube (DF) et la surface ACGE
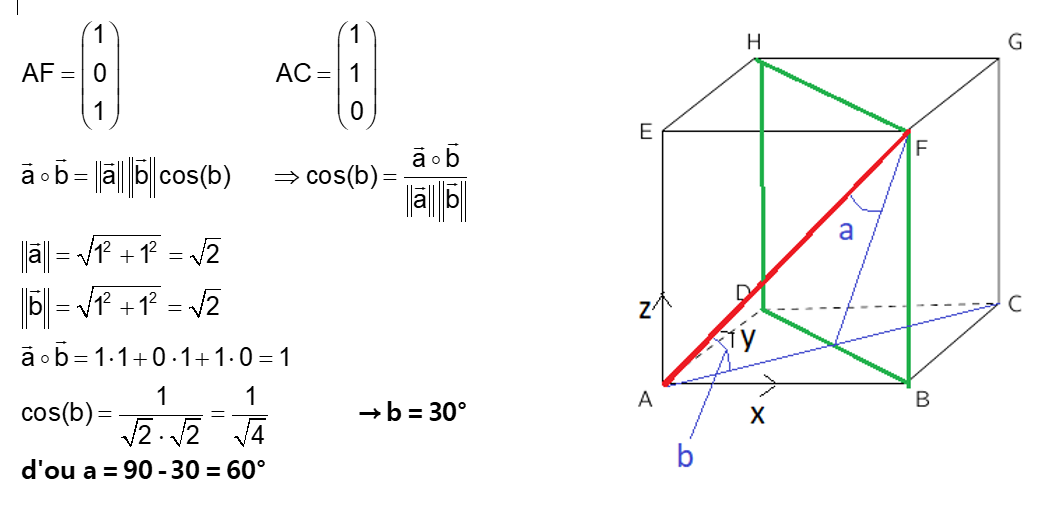
2) la diagonal de face (AF) et la surface BFHD
3) La diagonale (CE) et la surface AFH

Je sais qu'on peut trouver l'angle avec la formule du produit scalaire et sortir le cosinus mais je vois pas comment trouver le vecteur se trouvant sur les surfaces ACGE et BFHD.

Merci d'avance pour votre aide!
-----

[gg0]

En fait, l'angle entre une droite et un plan est l'angle entre la droite et sa projetée sur le plan, donc il te suffit, dans le premier cas, de trouver les projetés de D et F sur le plan.

Bon travail !

[pyrosman]

Je comprends bien merci mais comment projeté mon vecteur (DF) sur la surface ACGE?
Dans le cas ou on prends le plan xy ou xz ou yz c'est facile il suffit de mettre la composantes qu'on ne veut pas à 0 mais dans le cas ou on veut projeter sur un plan qui n'est pas un de ces plans "faciles" comment s'y prendre?

[gg0]

Il te faut trouver les projetés de D et F. Pour D, tu cherches quelle est la droite passant par D qui est perpendiculaire au plan (ACGE). C'est assez évident, et tu obtiendras le projeté de D.
On peut aussi utiliser un repère orthonormé basé sur les sommets du cube, et utiliser des équations de droites et de plans, mais ça me semble plus lourd à réaliser.

[A voir en vidéo sur Futura]

[pyrosman]

Voila ce que j'ai fait. Je pense que c'est correct. Y a t'il un moyen plus simple?

[pyrosman]

Et voila pour le deuxième, mais ça me semble très compliqué à nouveau. Y a pas une méthode plus facile?

[pyrosman]

Et je coince pour le dernier :
3) La diagonale (CE) et la surface AFH

[gg0]

Pour la dernière, la remarque CA=CF=CH et EA=EF=EH permet de régler la question immédiatement.

Cordialement.

[pyrosman]

Hum, je suis désolé mais je ne vois toujours pas :/ J'essaie de poser mes vecteurs et de projeter sur ce plan mais je ne vois pas comment faire.

Et il n'y a pas une autre méthode pour les 2 premiers que j'ai fait qui serait plus simple?

Merci d'avance!

[gg0]

Des points à égale distance, ça ne te rappelle rien ?
Dans le plan, les points équidistants de deux points A et B sont ...
Dans l'espace, des points équidistants de trois points non alignés A, F et H ...

NB : Pour l'instant, je ne peux pas lire tes pièces jointes, en cours de validation.

[ansset]

Je reviens juste la dessus :

Voici mon problème. Je bloque sur un exercice de géométrie de l'espace. On vient de finir le chapitre géométrie vectoriel avec les produits scalaires.

toutes tes questions peuvent être résolues en utilisant ce cours. ( applications directes)
pourtant, il semble que tu n'y fasse référence dans aucune de tes "démarches".

[ansset]

pour le c'est ok,mais il y a une erreur dans le second post. (d'ailleurs je comprend mal tes notations )
une autre manière de résoudre ce type d'exercice est de calculer l angle que fait la droite avec la normale au plan.
(car il peut y avoir des constructions plus complexes )
l'angle obtenu n'est pas celui recherché mais c'est son complémentaire entre0 et pi/2
ex ici pour les second exercice.
plan BFHD et droite AF
la droite AF( 1,0,1)
le plan peut être défini par deux vecteurs non colinéraires comme BF(0,0,1) et FH(-1,1,0)
un vecteur V perp au plan satisfait V.BF=0 et V.FH=0
on en déduit que (1,1,0) est perp au plan.
l'angle a entre AF et V est donné avec la relation que tu connais. ( en le prenant entre 0 et pi/2)
l'angle recherché vaut pi/2-a