Dans un de mes livres de logique je vois :
« Nous avons expliqué que les axiomes d'un système déductif sont "complets" si toute assertion vraie que l'on peut exprimer dans ce système est formellement déductible à partir des axiomes. »
Sur Wikipédia je vois :
« Un système de déduction pour une logique donnée (calcul propositionnel, ou calcul des prédicats en logique classique mais aussi en logique intuitionniste ...), est complet quand il démontre les formules valides dans tous les modèles de cette logique. »
Mais qui semble en contradiction avec le théorème de complétude de Gödel car d'après lui toute théorie serait complète, ce qui rend la complétude assez pauvre finalement.
Et dans un autre livre de logique, de ce que j'ai compris ils définissent ça comme "toute formule close est décidable dans la théorie".
Serait-ce que tout le monde ait raison mais que je n'aie pas compris grand chose ?
Merci à vous, bonne journée.
-----





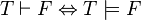
 soit démontrable"
soit démontrable"