Salut tous,
j'ai une question simple mais je ne suis pas certains de moi
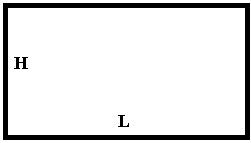
J'ai un carré (donc en 2D) et j'ai une loi de ce type:
qui peut également s'ecrire:
mais par contre dS sera quelle surface ?
- la surface totale de ce carré ?
- un des bords du carré ?
- la somme de tous les bords du carré ?
merci d'avance pour votre aide
-----