Gyroscope, couple et mouvement

[fl51]

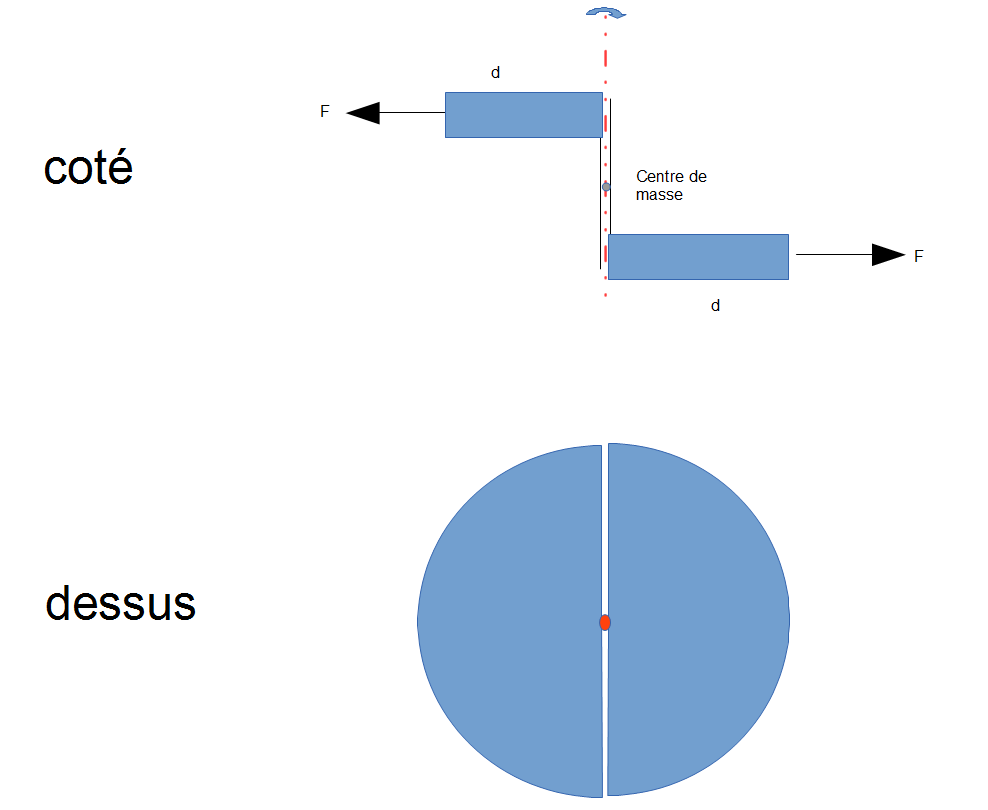
Bonjour, je suis nouveau sur le forum. J'ai une question sur le fonctionnement du gyroscope un peu particulier normalement composé d'un seul cylindre. Il est composé de deux demi cylindres figés entre eux sur l'axe de rotation. Pas de gravité ou de friction, c'est simplement une étude théorique. Les deux demi cylindres sont espacés "verticalement" sur l'axe. Le centre de masse se trouve bien sur l'axe de rotation du gyroscope. Au départ le gyroscope est fixé sur un support, je le lance à w rd/s cela me demande une certaine énergie. Je libère l'axe de tout support, chaque demi cylindre crée un couple, ce couple tend à mettre en rotation le gyroscope dans le plan perpendiculaire. Le gyroscope possède donc sa vitesse de rotation autour de son axe principal et une rotation supplémentaire (sur un autre plan) fournit par le couple. L'énergie du gyroscope peut être récupérée théoriquement en le brisant (récupération des énergie cinétiques de chaque particule). L'énergie étant conservée, j'ai plusieurs pistes mais aucune ne me satisfait:

- le couple change w, comment ?
- il n'y a pas de couple ou le couple est annulé par autre chose
- la nouvelle rotation n'augmente pas la somme des énergies cinétiques de chaque "particule"

Si vous pouvez m'éclairer ?




En tout cas, s'il y a un couple et 2 rotations, comment est le mouvement du gyroscope dans l'espace ?
-----

[calculair]

Bonjour,


Pour chaque 1/2 cylindre
Soit M le centre de masse et m la masse

soit O le point ou le 1/2 cylindre et attaché à l'axe

Le moment cinétique d est M = OM ^mV ou V est la vitesse tangentielle du centre de masse M

en devrivant /au temps

dM /dt = dOM/dt ^m V + OM ^m dV/dt

dOM /dt est le vecteur vitesse V comme dOM /dt et V sont colinéaire le produit vectoriel nul

il reste OM ^m dV/dt et m dV/dt est une force F et OM ^F est le moment de la force F / à l'axe

La force centripète exerce colinéaire à OM donne un couple nul

Les composantes de F non colinéaires à OM créent un couple qui tent à faire tourner dans la direction perpendiculaire àux compsantes de F ( non centripètes) et OM

On dit ainsi que la dérivée du moment cinétique = aux couples des forces apiqués

[LPFR]

Bonjour.
Premièrement, un objet ne peut pas avoir deux rotations. Il ne peut avoir qu'une seule.

Un objet libre dans l'espace ne peut tourner de façon stable qu'autour son axe d'inertie majeur ou autour de son axe d'inertie mineur.
Si vous lancez en l'air un objet parallélépipédique (avec ses trois dimensions différentes, comme les anciennes boites d'allumettes ou un paquet de cigarettes) en le faisant tourner, à chaque essai, autour de chacun de ses trois axes principaux, vous constaterez ce que je viens de vous dire. Il tournera sans problème autour de ses axes majeur et mineur, mais fera des "choses bizarres" autour de son axe intermédiaire.

Si on prend un objet comme le votre. Que l'on fait tourner autour de l'axe que vous donnez (en le tenant fermement) puis qu'on le lâche en apesanteur, il va se produire:
- L'énergie cinétique se conserve. C'est à dire le produit ½ Jw². Ou J est le moment d'inertie autour de l'axe de rotation.
- Le moment angulaire se conserve (direction et module). C'est à dire Jw (vecteur).
- L'objet va changer d'orientation tout en conservant l'axe autour duquel il tourne dans l'espace. Son axe de rotation ne sera plus celui du départ. Et ce changement d'orientation est sacrement compliqué (pour moi). Je pense qu'il s'appelle "nutation" mais je ne suis même pas sur du nom.

- Pendant ces changements, la vitesse angulaire changera ainsi que J qui va dépende de l'orientation de l'objet par rapport à l'axe de rotation.


Je me souviens d'avoir étudié ça au millénaire précédent. C'est loin et je n'ai jamais ré-touché depuis.
Au revoir.

[calculair]

Bonjour LPFR,

Tu as raison, l'étude complète du mouvement du gyroscope, est assez subtil, il me faudrait du temps pour décrypter les démonstrations sur ce sujet.

Il faut considérer 3 mouvements

La rotation autour de l'axe principal ( disons l'axe de la toupie)

L'axxe principal tourne c'est la précession

autour de la trajectoire de précession il y a des oscillations, c'est la mutation, je crois qu'elle apparait quand la vitesse de précession n'est plus négligeable devant la vitesse de rotation autour de l'axe principal.

Je ne saurais pas refaire la démonstration, et il me faudrait sans doute 1 heures ou 2 pour comprendre une démonstration sur ce sujet...Je crois que d'illustres mathématiciens qui se sont penches sur le mouvement du gyroscope ont mis plusieurs dizaines d'année pour établir la démonstration.

[A voir en vidéo sur Futura]

[fl51]

Bonjour,

Merci pour vos réponses.

Premièrement, un objet ne peut pas avoir deux rotations. Il ne peut avoir qu'une seule.

Je croyais qu'un gyroscope avait 2 rotations lorsqu'il subissait un couple. En réalité, il n'y a qu'une seule rotation ?

[LPFR]

Re.
Oui. Il n'y a qu'une seule. Même si l'axe de rotation change en fonction du temps, comme dans la précession.
A+

[fl51]

Lorsqu'il précessione, c'est une illusion d'optique ?

[LPFR]

Re.
Pas du tout !
C'est tout ce qui a de vrai.
A+

[Amanuensis]

- L'énergie cinétique se conserve. C'est à dire le produit ½ Jw². Ou J est le moment d'inertie autour de l'axe de rotation.
- Le moment angulaire se conserve (direction et module). C'est à dire Jw (vecteur).
- L'objet va changer d'orientation tout en conservant l'axe autour duquel il tourne dans l'espace. Son axe de rotation ne sera plus celui du départ.

Bizarre...

a) Dans le cas général faut travailler avec le tenseur J: la relation entre le vecteur rotation w et le moment cinétique est donnée par un tenseur, pas par un scalaire (ils ne sont pas nécessairement colinéaires).

b) faut distinguer la notion d'axe de rotation (la direction de w) dans le référentiel inertiel et celui par rapport à l'objet. On peut par exemple écrire le moment cinétique (dans le référentiel inertiel) comme JRw, avec w le vecteur rotation, R une matrice de rotation dépendant de l'orientation (changement de repère) et J la matrice du tenseur d'inertie (invariante, dépendant de la forme de l'objet). En écrivant J'w, J' dépend de l'orientation puisqu'on travaille dans le référentiel inertiel.

c) L'énergie est 1/2 (J'w).w, avec J' le tenseur (relativement au référentiel inertiel, le prime pour distinguer de J invariant, relativement à l'objet) et "." le produit scalaire.

Notons que ce qui se conserve est le moment cinétique dans un référentiel inertiel, ce qui fait que la direction de w relativement au référentiel inertiel n'est pas nécessairement conservée, la relation entre rotation et moment cinétique n'étant pas scalaire. On ne peut donc pas parler de la conservation de Jw avec J un scalaire qui dépendrait de l'orientation ; encore moins de J(w²).

Enfin, on peut parler de la rotation du vecteur w (quand sa direction n'est pas conservée), et donc d'une certaine manière de deux rotations: celle de l'objet, et celle de l'axe de rotation de l'objet par rapport au référentiel inertiel. (Sans compter le mouvement de l'axe de rotation par rapport à l'objet...)

[fl51]

Il y a donc bien 2 rotations ? Si c'est le cas les vecteurs vitesses étant perpendiculaires il y a augmentation de l'énergie, non ? Donc pour la conservation de l'énergie, j'ai pensé que lorsque le gyroscope est mis au fur et à mesure en rotation il demande plus d'énergie mais il est possible de "lancer" les 2 demis cylindres à V et -V pour qu'ils se rencontrent, cela demande deux fois 1/2mv², une fois cette vitesse atteinte on peut les mettre en rotation. C'est donc la rotation principale w qui diminue ?

[LPFR]

Re.
Bons, je pense qu'il est temps que j'arrête. La mention de l'augmentation de l'énergie me fait craindre que fl51 soit parti vers un "mobile perpétuel".

De plus, le solide avec les deux demi cylindres s'avère pas si solide puisque maintenait il veut les lancer l'un contre l'autre.
Ça me suffit. J'arrête.
A+