Aire d'un quadrilatère quelconque

[update222]

Bonjour,

J'aimerais savoir s'il est possible de calculer l'aire d'un quadrilatère quelconque en connaissant uniquement les longueurs de ses 4 cotés.

Merci beaucoup
-----

[danyvio]

Ce n'est pas possible, car un quadrilatère quelconque est "déformable", et selon qu'il est aplati (aire=0) ou non, son aire varie... Dans ton cas il faut connaître, en plus des côtés, la mesure d'un angle.

[danyvio]

Ce n'est pas possible, car un quadrilatère quelconque est "déformable", et selon qu'il est aplati (aire=0) ou non, son aire varie... Dans ton cas il faut connaître, en plus des côtés, la mesure d'un angle.

Pardon de me citer. Mais on peut résoudre le problème si, au lieu d'un angle, on connaît une diagonale...

[Tryss]

Pardon de me citer. Mais on peut résoudre le problème si, au lieu d'un angle, on connaît une diagonale...

Ça ne suffit pas.

Un quadrilatère dont les cotés font :

AB = 3, BC = 3, CD = racine(5), DA = racine(5) et, au choix ABC = 90° et/ou AC = 3 racine(2) a deux aires possibles :

- une aire égale à 6 si le quadrilatère est convexe
- une aire égale à 3 si il ne l'est pas

De même avec celui là :

AB = 1, BC = racine(2), CD = 1, DA = racine(2) et AC = 1 et/ou ABC = 45°

- Une aire égale à 1 si le quadrilatère est convexe (un joli parallélogramme)
- Une aire égale à 1/2 si le quadrilatère est croisé

[A voir en vidéo sur Futura]

[update222]

Désolé, mais j'avais oublié une donnée importante du problème:
il s'agit de trouver l'aire *maximale* d'un quadrilatère de cotés a,b,c,d.
et on peut ajouter non croisé.

merci d'avance

[danyvio]

Désolé, mais j'avais oublié une donnée importante du problème:
il s'agit de trouver l'aire *maximale* d'un quadrilatère de cotés a,b,c,d.
et on peut ajouter non croisé.

merci d'avance

Alors il faut trouver l'angle optimal (par exemple ceui qui est adjacent à a et b. Il y a du sinus dans l'air (et même dans l'airE )

[update222]

Sûrement, mais j'ai du mal à trouver la formule donnant la surface à partir des 4 cotés connus et un angle à optimiser.
je ne connais pas du tout les diagonales.
Quelqu'un peut m'aider?

[danyvio]

Dans ce genre de problème il faut se ramener en général à découper en triangles.

A partir du moment où tu connais deux côtés adjacents (par ex a et b), tu peux calculer EN FONCTION DE L'ANGLE la diagonale (= le troisième côté du triangle a,b, et ce qui relie les extrêmités de a et b. Il existe une formule pour calculer l'aire de ce triangle. Tu appliques cette même formule au triangle composé de cette même diagonale et des côtés c et d . Additionner les deux formules pour avoir l'aire totale.
La formule trouvée contiendra l'inconnue "angle séparant a et b". Tu dériveras pour obtenir le mini et le maxi. Et hop c'est plié...

[update222]

j'ai les relations:
S(ABC)=1/2 AB.BC.sin(ABC)
S(ADC)=1/2 AC.AD.sin(ADC) avec AB,BC,AC,AD les 4 cotés connus
mais les 2 angles ne sont pas identiques.
j'ai pour la diagonale:
AC²=AB²+BC²-2.AB.BC.cos(ABC)
AC²=AD²+DC²-2.AD.DC.cos(ADC)
pour la relation donnant ADC en fonction de ABC cela donne une grosse relation en ADC=acos(........cos(ABC)/....)
au final S(A)=1/2.a.b.sinA+1/2.c.d.sin(acos((a²+b²-2.a.b.cosA)/(d²+c²-2.d.c)))
y'a pas plus simple à dériver?

[update222]

la dérivée de h°g°f c'est quoi ? [h'°(g°f)].(g'°f).f' ?

[danyvio]

Autre piste (sans garantie) :

On prend comme variable cette fameuse diagonale commune aux deux triangles.
1) elle a un domaine de définition car, comme tout côté d'un triangle elle a une mesure positive entre la somme et la différence des deux autres côtés. Petite difficulté : ce doit être vérifié simultanément pour les deux triangles accolés.

2) En respectant ci dessus, tu as facilement l'aire des deux triangles accolés (rappel de la formule générale de l'aire d'un triangle connaissant des 3 côtés a,b,c , où p est le demi-périmètre : S= racine carrée de p(p-a)(p-b)(p-c)

3) on dérive en fonction de la mesure de la diagonale.

[danyvio]

Ce serait sympa de nous indiquer la correction de ce problème.

[mécano41]

Bonjour à tous,

Lorsque l'on fait déjà le calcul de la position d'un côté en bougeant le côté opposé on arrive déjà à un truc un peu tordu...alors pour la suite...

Dans l'appli. EXCEL jointe, j'ai mis le calcul indiqué ci-dessus (attention, comme il faut faire un choix de solutions, il est possible que celles que j'ai choisies ne conviennent pas dans tous les cas de figures.


Ceci permet de déterminer les positions de deux sommets, les deux autres étant fixes. Ensuite, j'ai calculé la surface des deux triangles formés (produit vectoriel divisé par deux) et pour le maxi, j'ai utilisé le solveur (je n'ai pas automatisé donc il faut relancer le solveur à chaque modif des longueurs de côtés)
En haut à droite, le calcul de alpha pour trois sommets alignés est fait pour donner une limite au solveur ; selon le cas d'impossibilité s'il y a lieu, il faut indiquer la valeur comme alpha maxi ou comme alpha mini.

Le solveur sort l'angle donc la position des sommets pour l'aire maxi.

Si UPDATE22 a besoin d'une formule unique, je ne sais pas faire...sinon, cela peut lui servir....


Cordialement

[mécano41]

Bonjour,

Je mets un nouveau fichier ; la recherche de sin beta et cos beta a été rendue plus claire (le bon quadrant est trouvé automatiquement).
D'autre part, j'avais inversé la désignation des produits vectoriels par rapport au calcul...

Ne pas oublier de relancer le solveur à chaque modif. des longueurs des côtés du quadrilatère...ce n'est pas automatique...

Cordialement

[update222]

J'ai trouvé une formule qui marche mais sans démonstration par extension de celle du triangle:

Soit s=(a+b+c+d)/2 avec a,b,c,d les dimensions des côtés du quadrilatère,

L'aire maximum du quadrilatère est: A=sqrt((s-a)*(s-b)*(s-c)*(s-d)) où sqrt est la racine carrée.

[Igorkis]

Bonjour, je pense qu'il est possible de le calculer en le planchant dans un repère, comme ceci: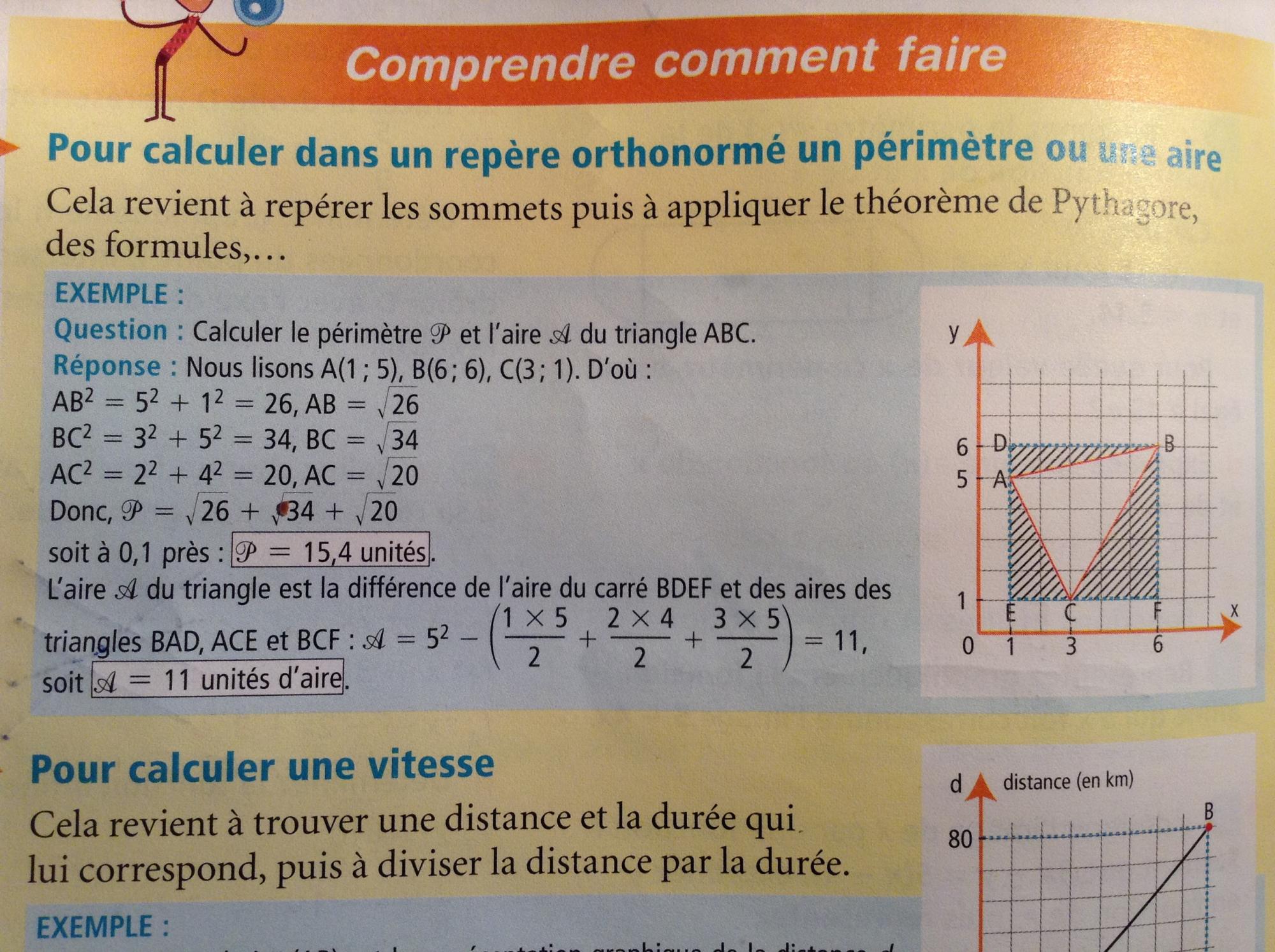

[gg0]

1) répondre à un sujet 2 ans et 2 mois après montre qu'on ne sait pas bien lire
2) D'ailleurs le sujet n'a rien à voir avec cette page d'un ouvrage d'école.

[MimiDjzry]

Bonsoir,

Je suis en 4eme et mon prof de math ma demander de calculer l'air d'un quadrilatere IJKL
IJ=6.8
IL=5.1
JK=6.5
La mesure de KL je ne la connais pas.
Vous pouvez m'aider sil vous plait!? Merci pour ceux qu'il répondront

[Tryss]

Le problème n'a pas de solution : l'aire peut valoir 0 (IJKL alignés) comme plus de 40...

[MimiDjzry]

Mercii beaucoup!

[gougougou]

On peut calculer l'aire d'un quadrilatère convexe connaissant les longueurs des 4 côtés et la valeur d'un angle.

DEMONSTRATION:
Calcul de l’aire S du quadrilatère convexe ABCD connaissant les longueurs des 4 côtés et la valeur de l’angle DAB notée α

Comme on le voit sur un dessin l’aire S du quadrilatère est la somme de l’aire S1 du triangle DAB et de l’aire S2 du triangle BCD

L’aire du triangle DAB est donnée directement par la formule générale Aire = 1/2 (a x b sin α) :
S1 = 1/2 AB x AD sin α

Pour calculer l’aire de BCD, on calcule d’abord la longueur du côté BD, qui est également côté du triangle DAB. La formule d’Al Kashi nous donne :
DB2 = AB2 + AD2 -2AB x AD cos(α)
Donc DB = Racine (AB2 + AD2 - 2AB x AD cos α )

Appliquons maintenant la formule consacrée pour le calcul de l’aire S2 du triangle BCD en fonction de la longueur des 3 côtés

S2 = 1/4 x (Racine( (BC+CD+DB) x (-BC+CD+DB) x (BC-CD+DB) x (BC+CD-DB) )

En reportant la valeur de DB calculée plus haut:

S2 = 1/4 x (Racine( (BC+CD+ Racine (AB2 + AD2 -2AB x AD cos α )) x (-BC+CD+ Racine (AB2 + AD2 -2AB x AD cos α )) x (BC-CD+ Racine (AB2 + AD2 -2AB x AD cos α )) x (BC-CD+ Racine (AB2 + AD2 -2AB x AD cos α )) )

L’aire du quadrilatère ABCD d’angle α en A est S = S1 + S2
S = S1 = 1/2 AB x AD sin α + 1/4 x (Racine( (BC+CD+ Racine (AB2 + AD2 - 2AB x AD cos α )) x (-BC+CD+ Racine (AB2 + AD2 - 2AB x AD cos α )) x (BC-CD+ Racine (AB2 + AD2 - 2AB x AD cos α )) x (BC-CD+ Racine (AB2 + AD2 - 2AB x AD cos α )) )

Salutations
Gougougou

[gougougou]

On peut calculer l'aire d'un quadrilatère convexe connaissant les longueurs de côtés et un angle.

DEMONSTRATION:
Calcul de l’aire S du quadrilatère convexe ABCD connaissant les longueurs des 4 côtés et la valeur de l’angle DAB notée α

Comme on le voit sur un dessin l’aire S du quadrilatère est la somme de l’aire S1 du triangle DAB et de l’aire S2 du triangle BCD

L’aire du triangle DAB est donnée directement par la formule générale Aire = 1/2 (a x b sin α :
S1 = 1/2 AB x AD sin α

Pour calculer l’aire de BCD, on calcule d’abord la longueur du côté BD, qui est également côté du triangle DAB. La formule d’Al Kashi nous donne :
DB2 = AB2 + AD2 -2AB x AD cos(α)
Donc DB = Racine (AB2 + AD2 - 2AB x AD cos α )

Appliquons maintenant la formule consacrée pour le calcul de l’aire S2 du triangle BCD en fonction de la longueur des 3 côtés

S2 = 1/4 x (Racine( (BC+CD+DB) x (-BC+CD+DB) x (BC-CD+DB) x (BC+CD-DB) )

En reportant la valeur de DB calculée plus haut:

S2 = 1/4 x (Racine( (BC+CD+ Racine (AB2 + AD2 -2AB x AD cos α )) x (-BC+CD+ Racine (AB2 + AD2 -2AB x AD cos α )) x (BC-CD+ Racine (AB2 + AD2 -2AB x AD cos α )) x (BC-CD+ Racine (AB2 + AD2 -2AB x AD cos α )) )

L’aire du quadrilatère ABCD d’angle α en A est S = S1 + S2
S = S1 = 1/2 AB x AD sin α + 1/4 x (Racine( (BC+CD+ Racine (AB2 + AD2 - 2AB x AD cos α )) x (-BC+CD+ Racine (AB2 + AD2 - 2AB x AD cos α )) x (BC-CD+ Racine (AB2 + AD2 - 2AB x AD cos α )) x (BC-CD+ Racine (AB2 + AD2 - 2AB x AD cos α )) )

Nota: AB2 signifie AB au carré

Salutations
Gougougou

[dceuppens1958]

Bonjour,

Il faut connaître au moins un des 4 angles du quadrilatère pour calculer la mesure de son aire.

La formule de Brahmagupta permet de calculer son aire maximale sur base de son périmètre.

l'aire A d'un quadrilatère de côtés a; b, c et d est donnée pa la formule suivante

A=racine carrée de ((s−a)(s−b)(s−c)(s−d))

avec "s" étant le demi périmètre du quadrilatère a, b, c, d
s = (a+b+c+d)/2

[jacknicklaus]

Bonjour,

pourquoi répéter, 9 ans après, le message #15 qui dit la même chose ??

[dceuppens1958]

Bonjour,

Ma réponse certes tardive est motivée par deux éléments dont vous semblez ne pas disposer.

1. je viens de m'inscrire sur ce forum que je quitterai sans doute rapidement vu l'accueil réservé

2. ma réponse diffère de la #15 car nonobstant le fait que j'y répète la formule donnée de façon "singulière" je précise qui en est l'auteur (Brahmagupta) et je précise également (car je ne pense pas l'avoir vu dans la réponse #15) qu'il s'agit d'une formule permettant de calculer l'aire maximale d'un quadrilatère quelconque en se basant sur son demi périmètre ainsi que le longueur de ses côtés.

Bien à vous