Bonjour à tous,
Avant de commencer j'aimerais vous demander d'ores et déjà d'être indulgentsje prévois une reprise d'études l'an prochain et je n'ai pas fait de maths depuis 10 ans (déjà !)
Donc venons-en à ma question. Au décours d'un exercice on me demande de calculer une dérivée et de la factoriser. Voici la correction :
Le problème c'est que pour moi factoriser de cette manière n'a rien d'évident. Ce n'est pas que je ne comprends pas : je vois bien que c'est juste, je vois bien que si je développe je retombe sur mes pattes. Mais j'aurais été incapable de passer de la seconde expression à la troisième puis la quatrième.
Ce que j'ai su faire c'est transformer le numérateur en polynôme du second degré, calculer ses racines, et factoriser sous la forme a(x-x1)(x-x2), mais c'est "de la triche" puisque dans la correction ils ne passent pas par ces étapes.
Comment faire pour arriver à "penser" à factoriser comme ça ?Ce n'est pas quelque chose qui saute aux yeux.
Question subsidiaire : pourquoi me demander de factoriser ? La suite de l'exercice consiste simplement à dresser le tableau de variation, et on a pas besoin de factoriser la dérivée pour cela, faire apparaitre le polynôme et trouver ses racines permet de résoudre l'exercice. Il y a donc sans doute un intérêt pédagogique derrière.
Pour info l'énoncé et la correction sont ici (exercice II, question 2) :
https://www.lyceedadultes.fr/siteped...06_11_2017.pdf
https://www.lyceedadultes.fr/siteped...correction.pdf
D'avance merci.
-----



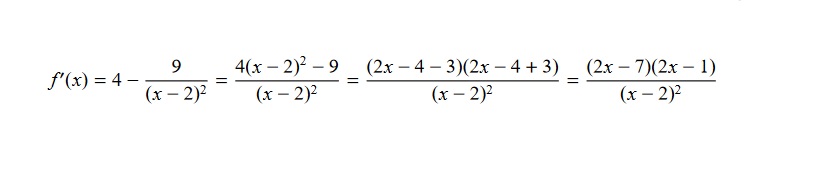
 et
et 

