Bijection entre deux variétés topologiquement différentes

[geometrodynamics_of_QFT]

Bonjour,

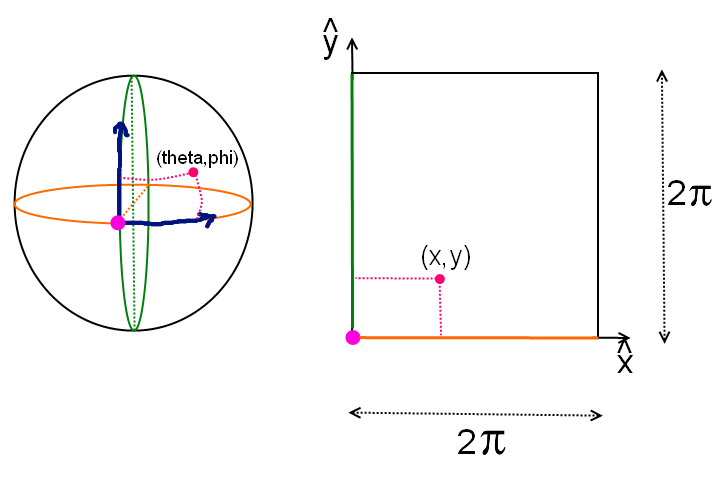
Je me pose la question de savoir s'il est envisageable de trouver une application linéaire bijective qui établit une correspondance 2 à 2 entre un point d'un carré (plan) "périodique" de côtés 2pi, et la surface d'une sphère.

Donc, pouvoir associer à chaque point (x,y) avec x et y dans [0, 2pi], un couple (theta, phi) correspondant à un point sur la sphère.

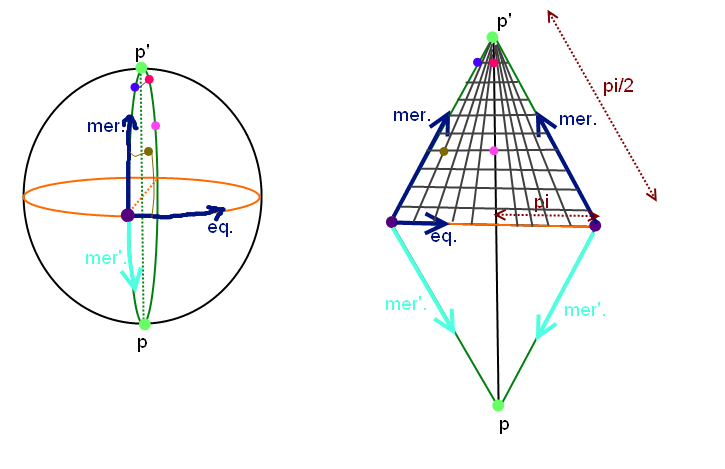
J'ai réalisé un petit brouillon de dessin afin que l'on puisse voir d'un coup d'oeil l'idée générale.

Puisque le carré et a sphère ont tous les deux une surface finie, il doit bien exister une telle bijection?

Je vous remercie d'avance pour vos réponses


-----

[geometrodynamics_of_QFT]

Bon, oui, il y a la projection stéréographique en général...mais on sait que le pôle nord se retrouve à l'infini...ce qui pose problème...

J'ai vu aussi ici que : (quelqu'un s'est posé la même question que moi )
"S2 is compact. A continuous image of a compact set is compact. R2 is not compact, so R2 cannot be a continuous image (let alone a continuous bijection) of S2."

Donc l'argument est de dire que S2 est compact, R² ne l'est pas. Donc une bijection est impossible car une image continue d'un ensemble compact est compacte.

Mais en même temps...la projection stéréographique est un contre-exemple? Puisqu'elle établit effectivement une telle bijection...???

[geometrodynamics_of_QFT]

Et puis aussi, une surface carré dans R², ce n'est pas R²...
La surface carrée finie (de côté 2pi) est-elle compacte?

J'ai parcouru l'article Wikipedia sur la compacité, mais comment vérifier pratiquement qu'une surface finie dans R² est compacte ou non?
A priori elle est semi-compacte (j'ai vu dans les exemples)...mais qu'est-ce que cela implique pour la possibilité de la bijection continue?

[gg0]

Bonjour.

Une application linéaire, non, puisque ce ne sont pas des espaces vectoriels. Une bijection, sans problème, puisque ce sont des ensembles de même cardinal. Mais il reste à expliciter, ce qui est loin d'être évident; et des points proches peuvent avoir des images éloignées. Une bijection continue (au sens habituel), difficile à faire puisque le carré a un bord, pas la sphère. D'ailleurs, tout dépend comment tu définis ton carré. En éliminant deux côtés consécutifs, on obtient une surface non compacte, mais qui se recolle (bord ouvert avec le bord fermé opposé); problème : On obtient un tore, pas une sphère. Le carré fermé (avec ses 4 côtés) est compact, mais on ne voit pas quoi faire de ces 4 bords !

Dernière chose : la projection stéréographique ne donne pas une bijection. Il manque un point à la sphère.

Cordialement.

[A voir en vidéo sur Futura]

[ansset]

la pièce jointe du début n'est pas accessible.
donc difficile de bien comprendre le pb.
ceci dit, nul besoin de stéréo pour faire une bijection.
celle ci est "connue" ( ou une de celle possible ) en image de synthèse en prenant un cube de 6 faces ( facile à calculer ) et en déduire le point en phi,theta d'un angle de vue.
très utile à la fois pour différents type d'éclairages indirects , ou pour réaliser des "textures projetées".
mais je crains ( faute d'avoir vu la pièce jointe ) que ce ne soit pas aussi simple.
sinon , c'est évident. ( même au pôle )
( pas besoin de passer par les quaternions ou autres pour cela )

[geometrodynamics_of_QFT]

Bonjour.

Merci

Une application linéaire, non, puisque ce ne sont pas des espaces vectoriels.

De fait.

tout dépend comment tu définis ton carré. En éliminant deux côtés consécutifs, on obtient une surface non compacte, mais qui se recolle (bord ouvert avec le bord fermé opposé); problème : On obtient un tore, pas une sphère. Le carré fermé (avec ses 4 côtés) est compact, mais on ne voit pas quoi faire de ces 4 bords !

Ok, donc tout se joue dans la définition des conditions aux limites du carré.
Les quatre coins du carré se confondent en un seul point sur la sphère, par exemple?
Pour un tore, les côtés opposés se confondent, sans varier la longueur de ceux-ci.
Ici, les longueurs des côtés (confondus 2 à 2 comme pour le tore) tendent vers 0 à mesure de la "transformation continue" en sphère...

Ou alors, à partir de 2 triangles?
le premier triangle, qu'on enroule pour former l'hémisphère nord, et le second pour l'hémisphère sud?
Les deux points de la base du triangle sont confondus, et le sommet reste au pôle...(un cône arrondi lol)
Et les deux côtés du triangle autres que la base se confondent aussi.

Donc pour la sphère totale, à partir d'un losange (dont une diagonale devient l'équateur)...donc un carré

Dernière chose : la projection stéréographique ne donne pas une bijection. Il manque un point à la sphère.

de re-fait

[ansset]

je ne comprend tj pas ou est le pb ! car il y a des continuités.

edit: mess croisés.

[geometrodynamics_of_QFT]

(un cône arrondi lol)

Un dôme ^^
rogntidjûûû

[geometrodynamics_of_QFT]

ceci dit, nul besoin de stéréo pour faire une bijection.
celle ci est "connue" ( ou une de celle possible ) en image de synthèse en prenant un cube de 6 faces ( facile à calculer ) et en déduire le point en phi,theta d'un angle de vue.

Ah oui en effet, bien vu ^^ donc un peu comme placer une source lumineuse au centre du cube, et une sphère qui entoure le cube...et voir par quel point du cube passe un rayon issu de tel point de la sphère...si je comprends bien.
Ben voilà, c'est réglé! C'était un peu l'idée de la correspondance entre le cube I^n et la boule B^n dont parlait Azizovsky...avec l'histoire des normes euclidienne ou "infini".

il ne reste plus qu'à trouver une bijection de la surface d'un cube vers une surface du plan R²...Ou de renormaliser différemment les distances sur la surface du cube pour qu'elles soient proportionnelles avec le même facteur de proportionnalité aux distances sur la sphère.
Car à la base, c'était pour résoudre le problème de Thomson dans le plan, et ensuite transporter la solution (grâce à la bijection) vers la sphère...

[gg0]

Tu n'as toujours pas défini ce que tu appelles un carré, ni le genre d'application que tu veux.

[geometrodynamics_of_QFT]

Tu n'as toujours pas défini ce que tu appelles un carré, ni le genre d'application que tu veux.

?? Vous voulez que je définisse un carré?

Et, vous m'avez rappelé vous-même qu'il ne s'agissait pas d'une application, puisqu'il ne s'agissaient pas d'espaces vectoriels...

Je désire une bijection de la sphère, vers une surface euclidienne fermée, sans bords.

Donc vers une losange, comme j'expliquais dans le message #6, ou alors vers un carré dont les 4 coins se confondent sur la sphère.
Ou alors vers un cube, comme le suggérait ansset et azizovsky, mais dans ce cas..cela poserait un soucis pour le problème de Thomson, car par exemple 2 points sur la sphère distants de D seront issus de 2 points ayant une distance différente suivant qu'ils sont sur la même face, ou sur 2 faces différentes (du cube..)
Voyez-vous ce que je veux dire?

[gg0]

"?? Vous voulez que je définisse un carré?" Non, mais que tu définisses ce qui est dans le carré ou pas (pour une bijection, il est fondamental de connaître exactement l'ensemble). Relis mon message #4 où je parle de plusieurs surfaces qu'on peut appeler "carré". je n'y évoque pas une surface ouvert, l'intérieur du carré, qu'on appelle aussi un carré. J'imagine qu'il ne s'agit pas du carré "ligne", constitué des 4 côtés uniquement ou encore du carré formé seulement par 4 points.

Cordialement.

[geometrodynamics_of_QFT]

J'y réponds dans le message #6 il me semble...
Quand je parle du losange...(les 2 triangles juxtaposés par la base, un pour chaque hémisphère)

En transformant le losange en carré :
On a le coin inférieur gauche qui correspond au pôle sud, le coin supérieur droit qui correspond au pôle nord, la diagonale qui va du coin supérieur gauche au coin inférieur droit qui correspondra à l'équateur...et qui mesure donc 2pi.
Donc le coin supérieur gauche et le coin inférieur droit sont confondus lorsqu'ils sont sur la sphère.
Et le côté supérieur se confond avec le côté droit, de même que le côté inférieur se confond avec le côté gauche.

Le domaine exact du carré serait
- pour la coordonnée horizontale x : [0, 2pi/sqrt(2)[
- pour la coordonnée verticale y : ]0, 2pi/sqrt(2)]

[gg0]

Dans le message #6 il n'était plus question de bijection, donc je n'avais pas compris.

Maintenant que je vois le dessin du message #1, la réponse est non, puisqu'il n'y a pas de longitude pour les deux pôles. Sinon, il y a bien une bijection entre la sphère privée de ses pôles et le carré privé de ses 3 côtés. Et l'application n'est pas continue au voisinage de la longitude 0.

Cordialement.

[geometrodynamics_of_QFT]

Dans le message #6 il n'était plus question de bijection, donc je n'avais pas compris.

Maintenant que je vois le dessin du message #1, la réponse est non, puisqu'il n'y a pas de longitude pour les deux pôles. Sinon, il y a bien une bijection entre la sphère privée de ses pôles et le carré privé de ses 3 côtés. Et l'application n'est pas continue au voisinage de la longitude 0.

Cordialement.

Ok merci...et concernant le "mapping" suggéré dans le message #13?

[ansset]

je vois aussi la première figure à l'instant.
on va vite dans ce cas se retrouver avec des pb topologiques dignes des cartographes

[geometrodynamics_of_QFT]

voilà un nouveau dessin pour illustrer...


(il est disponible ici aussi, si vous ne voulez pas attendre...)

[geometrodynamics_of_QFT]

Les flèches bleues portent à confusion :

Sur la sphère, la flèche équatoriale correspond à la flèche oblique sur le carré.
Sur la sphère, la flèche méridionale correspond aux flèches horizontales et verticales, qui se confondent lors du "repliement"

Mais dans ce cas, les côtés devraient mesurer 2pi/2, et non 2pi/sqrt(2)
il faudrait donc un carré de diagonale 2pi et de côté 2pi/2
(Donc un losange...)

[gg0]

Dans le message #13, l'expression "une surface euclidienne fermée, sans bords." est bizarre, veux-tu dire "une surface euclidienne fermée, sans son bord" ? Avec les triangles, il y a toujours un problème de continuité.
Autrement dit, il n'y a pas d'isomorphisme de variété différentiable avec un losange ou un carré.

Après, tout dépend de ce que tu veux faire de cette "projection".

[geometrodynamics_of_QFT]

Dans le message #13, l'expression "une surface euclidienne fermée, sans bords." est bizarre, veux-tu dire "une surface euclidienne fermée, sans son bord" ?

J'entends la même chose que ce qu'on entend lorsqu'on dit qu'un tore est une surface euclidienne fermée sans bords.

Avec les triangles, il y a toujours un problème de continuité.
Autrement dit, il n'y a pas d'isomorphisme de variété différentiable avec un losange ou un carré.

J'ai uploadé une image corrigée de ce que j'entends par projection à partir d'un losange:

(Elle est disponible ici aussi...)
Où est le problème de continuité? aux pôles? Mais ils correspondent à des coins...ça tombe bien?
Si on trace les parallèles, on voit que leur circonférence (sur la sphère) ou leur longueur (sur le losange) décroit continûment jusque 0...

Mais un problème de longueur apparaît directement : le côté du losange (qui est l’hypoténuse d'un triangle rectangle) doit être plus petite que la demi-petite diagonale (qui est un côté adjacent)...ce qui est vraisemblablement impossible en géométrie euclidienne?

Après, tout dépend de ce que tu veux faire de cette "projection".

Je veux tenter de résoudre le problème de Thomson dans le plan, puis ensuite utiliser cette bijection pour trouver la solution correspondante sur la sphère...

[geometrodynamics_of_QFT]

En fait, ne suffirait-il pas de munir le losange en question d'une métrique non-euclidienne? (et périodique?)
donc simplement, plutôt que ça soit un quadrillage qui épouse une courbure (qui est absente ici), c'est une quadrillage distordu sur un plan...

Un peu dans l'idée que ce que ça donne quand Gaston Lagaffe tire sur un fil de rideau en damier...et que le motif se distord (et que le rideau reste plan...(mais ses frontières se déforment))

[geometrodynamics_of_QFT]

Enfin je veux dire...munir le losange d'un métrique pour laquelle la contribution d'éléments de longueur dans une direction parallèle aux côtés est moindre que la contribution d'éléments de longueur dans une direction parallèle à la petite diagonale...

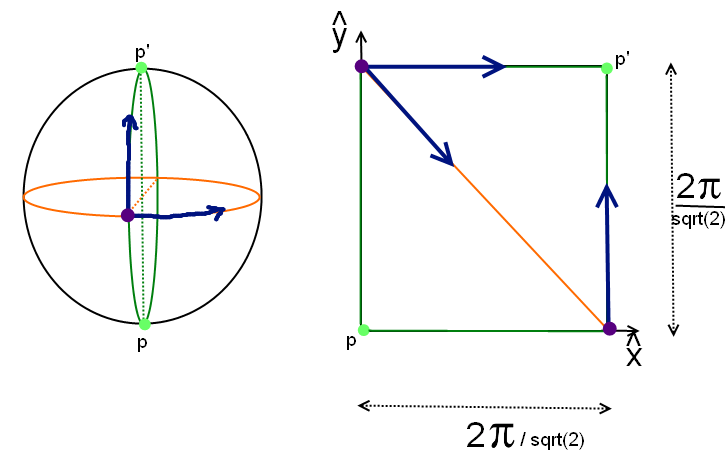
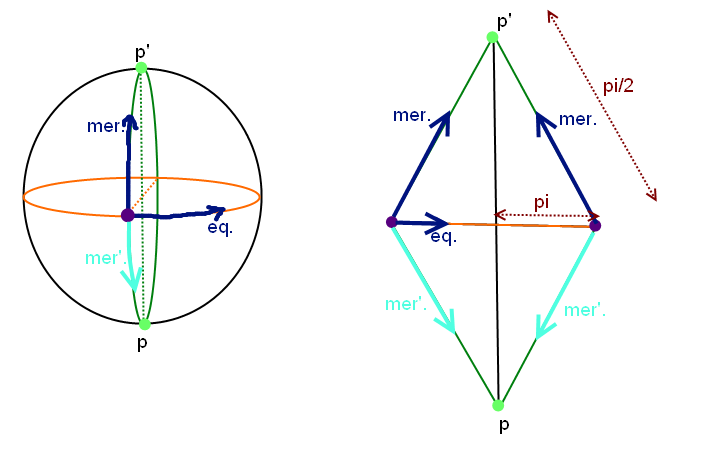
donc si on nomme ces deux directions pour la direction relative au côté supérieur gauche par exemple, et pour la direction parallèle à la petite diagonale (horizontale), on aurait quelque chose du style:

avec de manière à ce que le côté du losange puisse mesure pi/2 alors que la demi-petite diagonale mesure pi...

[geometrodynamics_of_QFT]

Ou de manière équivalente :

avec

[geometrodynamics_of_QFT]

(Tout ceci en choisissant comme vecteurs de base ces deux directions unitaires...qui correspondent aux grosses flèches bleues sur le dessin...c'est-à-dire à la longitude et à la latitude )

Je stoppe et j'attends vos réactions
Merci d'avance

[gg0]

Désolé, tu m'as perdu : Trop d'idées différentes en même temps.

C'est quoi, le problème de Thomson ?

Bonne chance !

[geometrodynamics_of_QFT]

Désolé, tu m'as perdu : Trop d'idées différentes en même temps.

C'est quoi, le problème de Thomson ?

Bonne chance !

il suffit de les lire de manière séquentielle, et pas toutes en même temps!
J'ai répondu à vos question dans le message #20

Le problème de Thomson, c'est trouver la position d'équilibre de N charges sur une sphère.

N'abandonnez pas svp

[geometrodynamics_of_QFT]

J'ai complété le dessin de manière à mettre en évidence la métrique non-euclidienne, et j'ai mis quelques points sur la sphère et la transformation que je propose:

*** Lien sur serveur externe ***
gg0, où-est ce que la continuité pose problème?

[azizovsky]

les cartographes savent qu'aucune portion, même petite, de sphère ne peut être appliquée sur un plan.
cela signifie qu'aucun changement de coordonnées ne peut transformer la première forme quadratique d'une sphère de rayon 1 en le forme .

[geometrodynamics_of_QFT]

les cartographes savent qu'aucune portion, même petite, de sphère ne peut être appliquée sur un plan.
cela signifie qu'aucun changement de coordonnées ne peut transformer la première forme quadratique d'une sphère de rayon 1 en le forme .

Oui mais justement!! N'est-ce pas différent ici?
Comme il était entrevu dans les messages #22 et #23, mais formulé d'un mauvaise manière.

Prenons la figure du message #27.
Assimilons votre à un déplacement infinitésimal le long du vecteur de base "eq." (flèche bleue) dans le losange.
Assimilons votre à un déplacement infinitésimal le long du vecteur de base "mer." dans le losange.

Dans ce cas, on observe que , en l'occurence la direction de change en fonction de sa coordonnée ...en passant par une direction verticale au milieu (correspondant au méridien opposé).

De même, la longueur ...(avec )

[geometrodynamics_of_QFT]

et