Formule de debordement/overflow ?

[invite6a95af8b]

Bonjour,

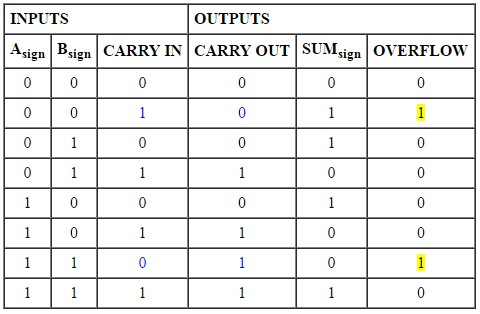
Je fait actuellement des études dans l'électronique, et j'ai une question à propos de la formule de débordement. De ce que j'ai compris, c'est la formule qui sert en cas d'addition de deux nombres sur n bits. Si la somme de ces deux nombres s'écrit sur n+1 bits, alors il y a débordement (ou overflow en anglais de ce que j'ai vu sur internet).

Mon problème, c'est que j'aimerais bien avoir la formule de cela justement, celle qui nous renvoie 1 si il y a débordement et 0 sinon par exemple. J'ai cherché sur internet français, et rien trouvé, et sur internet en anglais, j'ai trouvé un seul site qui me donne deux formules:

V = xk-1yk-1\sk-1 + \xk-1\yk-1sk-1 et V = ck-1 XOR ck-2 (source: http://www.cs.umd.edu/class/sum2003/.../overflow.html)

Le problème est que je ne comprend ni l'une ni l'autre, même avec les explications, pour la deuxième par exemple, quand j'essaie de l'appliquer avec ce que j'ai compris je ne trouve rien de cohérent.

Merci de votre aide.
-----

[jiherve]

Bonjour et bienvenue,
la seconde est très claire il suffit de faire un tableau mais d'autres l'ont déjà fait :http://www.c-jump.com/CIS77/CPU/Overflow/lecture.html
JR

[invite830075ec]

Bonjour,
Si x et y sont de signes différents il n'y a pas overflow car il y a autant de nombres positifs que négatifs.
xk-1yk-1\sk-1 est égal à 1 si x et y sont < 0 et s >= 0, overflow
\xk-1\yk-1sk-1 est égal à 1 si x et y sont >= 0 et s < 0, overflow
Les 2 cas étant exclusifs, leur somme fait 0 ou 1.

[invite6a95af8b]

Merci de vos réponses !

@jiherve

Après avoir regardé le site, je m'apperçois que c'est en fait la table de vérité que j'ai du mal à comprendre.



Pour être exact, c'est surtout quand je l'applique qu'il y a un problème pour moi, par exemple:

101
+011
---------
1000

Donc là j'ai overflow, et sur mon dernier calcul (donc la première colonne, pour calculer le MSB), j'ai: A=1; B=0; Carry In=1; Carry out=1 donc j'ai Carry In = Carry out donc normalement pas d'overflow d'après la formule. Du coup je crois que je n'ai pas du tout compris :/


@satinas

Ah je crois que j'ai compris la logique derrière cette formule, merci beaucoup ! Celle-ci était pas si compliquée en fait !

Merci.

[A voir en vidéo sur Futura]

[invite6a95af8b]

En fait même la première formule j'ai du mal avec la deuxième partie (la première est logique, si on additionne exactement deux 1 on part en overflow obligatoirement), mais la deuxième, je ne trouve pas: par exemple je veux faire:
011
+011
------
110

Donc pour la colonne de gauche, j'avais x=0, y=0 et s=1 donc d'après la formule (\xk-1\yk-1sk-1 surtout), je devrais avoir V = 1 et donc overflow, sauf que je ne l'ai pas là :/

[invite830075ec]

Il n' y a pas overfow si tu ajoutes un nombre négatif 101 à un nombre positif 011.

[invite830075ec]

Si tu ajoutes 2 nombres positifs, pas de problème tant que le résultat a son bit de poids fort à 0, le résultat est son toujours positif, dès qu'il passe à 1, il y a overflow, le processeur, pour lui positif, négatif c'est du pareil au même.

[jiherve]

Re
attention au codage si c'est signé (complément à 2) il y a overlfow (le signe du resultat n'est pas celui commun aux des deux entrées) si c'est non signé il n'y a pas overflow avec ton exemple
C'est bien expliqué sur le site.
JR

[invite830075ec]

Le bit carry le plus fort issu de l'addition (Sk), c'est l'overflow en addition non signée, pas en addition signée.

[invite6a95af8b]

Ah oui d'accord, donc en signé on a overflow si on change de signe au final c'est ça ?

Et du coup, en non signé, la formule change non ? Parce que si je code sur 4 bits en non signé et que je fait cette addition:

1100
+0111
---------
10011

Là mon résultat est codé sur 5 bits, donc je suis en overflow (vu qu'on ne prends pas en compte le signe, donc l'exception si les deux ont un signe différent ne fonctionne plus). Et ça correspondrait aux lignes 4 et 6 du tableau.

[invite830075ec]

En addition non signée, je dirais
V = Sk
V = S < x || S < y

[invite6a95af8b]

En relisant (encore) le site, on peut résumer: en signé, si c'est le même signe pour nos deux termes et que le terme de sortie n'est plus le même signe, alors on a overflow. En non signé, si on a carry out = 1 pour le MSB, alors overflow aussi (pour l'exemple que j'ai donné en haut). Du coup, le seul mystère qu'il reste à résoudre pour moi, c'est la dernière ligne du tableau en signé: Certes on obtient un nombre du même signe, donc pas d'overflow normalement, mais on le codera sur un bit de plus vu que carry out = 1 non ?

[invite830075ec]

J'ai pas regardé les tableaux, mais tu veux pas transformer un processeur 32 bits en processeur 33 bits, par hasard ?

[jiherve]

re
non car prenons -1 codé sur 8 bits = 1111 1111 + 1111 1111 =1 1111 1110 il y a bien une carry mais pas d'overflow car cela fait bien -2 les signes sont corrects.


JR

[invite6a95af8b]

Ah oui d'accord, merci à vous deux, je crois que je confondais carry et overflow en fait :/
En tout cas, c'est beaucoup plus clair maintenant, je pense avoir compris la notion, grâce à vous deux, donc merci beaucoup ! Vous m'avez beaucoup aidé !