Bonjour,
je modélise un bras robotisé
j'ai fait le modèle géométrique directe qui lie les cordonnées de l'effecteur (xyz (bout du bras)) au angles des articulations (t2,t3,t4)
j'aimerais inversé le système et obtenir une expression analytique du type t2=f(x,y,z) t3=g(x,y,z) t4=h(x,y,z) mais je n'y arrive pas:
Méthode que j'ai essayé :
paul
substitution cos = 1-u²/1+u²
-----



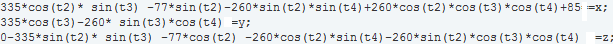
 est la fonction à inverser, alors, on peut recouvrir
est la fonction à inverser, alors, on peut recouvrir