C - 4c = 1/4 ?

[aWeZiMoBu]

Bonsoir,

Comme vous l'aurez probablement compris, le titre de mon post fait référence à la fameuse sommation de Ramanujan dans laquelle il trouve comme résultat -1/12 pour la série des entiers naturels qu'il appelle C.

C = 1+2+3+4+5+6+7+8+9+...

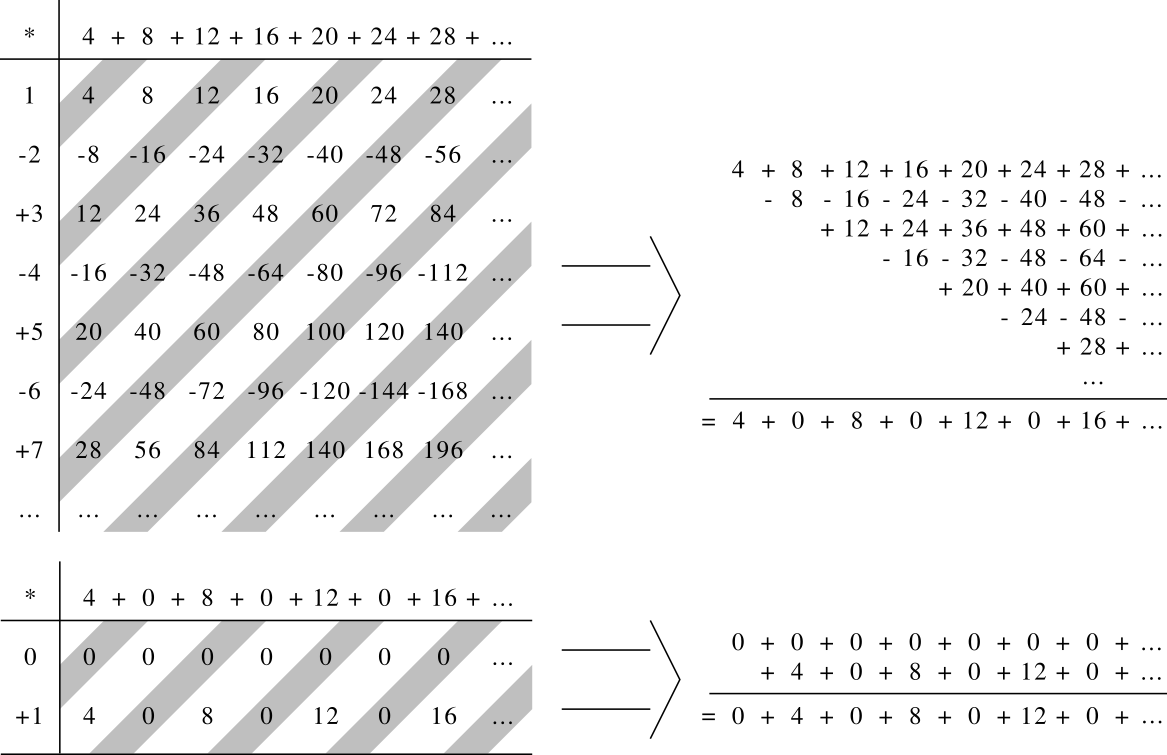
Ramanujan explique dans sa lettre que C - "4C" = 1/4

4C = 4+8+12+16+20+24+28+...

mais lui va soustraire 0+4+0+8+0+12+0+16+... à C, sauf que rien ne nous certifie que 0+4+0+8+0+12+0+16+... soit égale à 4+8+12+16+20+24+28+...

De plus, j'ai remarqué que

4+0+8+0+12+0+16+0+20-... = (4+8+12+16+20+24+28+...) * (1-2+3-4+5-6+7-8+9-...) = 4C * 1/4

Et (4+0+8+0+12+0+16+0+20-...) * (0+1) = 0+4+0+8+0+12+0+16+0+20-... ce qui fait qu'ajouter un ou plusieurs 0 au début d'une série ne change pas sa valeur.



Du coup, si mon raisonnement est juste, cela pose un sérieux problème sur la validité de sa sommation puisque C – 4C/4 = 1/4 revient à dire que C – C = 1/4*.

Personnellement, j'ai la conviction que C = (1-1)^-2, c'est-à-dire 1/(1-2+1), car cela permettrait d’expliquer tous les paradoxes que l’on trouve avec C.

Je serais ravi de connaître vos avis.

Merci
-----

[pm42]

sauf que rien ne nous certifie que 0+4+0+8+0+12+0+16+... soit égale à 4+8+12+16+20+24+28+...

Comme ça "rien ne le certifie" ? Il faudrait être plus précis parce qu'on a 2 séries divergentes. Donc il faudrait savoir comment on définit l'égalité entre elles.
Mais dans le cas présent, la plupart des définitions cohérentes feraient que la somme des 0 étant une série convergente égale à 0, on aurait de bonnes chances d'avoir l'égalité.

[aWeZiMoBu]

Comme ça "rien ne le certifie" ? Il faudrait être plus précis parce qu'on a 2 séries divergentes. Donc il faudrait savoir comment on définit l'égalité entre elles.
Mais dans le cas présent, la plupart des définitions cohérentes feraient que la somme des 0 étant une série convergente égale à 0, on aurait de bonnes chances d'avoir l'égalité.

Même si nous admettons que 4+8+12+16+... = 0+4+0+8+0+12+0+16+..., cela ne change rien à mon raisonnement. Au contraire, cela montre que 4c = 4c/4, ce qui est absurde sauf si c = 1/(1-1)².

[aWeZiMoBu]

Voici d'autres arguments qui me font penser que Ramanujan s'est trompé :

Il y a d'abord la table arithmétique étendue (triangle de Pascal).

tables arithmétique.png

Ensuite, il y a les séries convergentes, divergentes et alternatives suivantes.

1/-3 = 1/(-2)¹ + 1/(-2)² + 1/(-2)³ + 1/(-2)⁴ + ...
1/-2 = 1/(-1)¹ + 1/(-1)² + 1/(-1)³ + 1/(-1)⁴ + ... = -1+1-1+1-...
1/-1 = 1/0¹ + 1/0² + 1/0³ + 1/0⁴ + ... = (1+1+1+1+...) + (1+2+3+4+...) + (1+3+6+10+...) + (1+4+10+20+...) + ...
1/0 = 1/1¹ + 1/1² + 1/1³ + 1/1⁴ + ... = 1+1+1+1+...
1/1 = 1/2¹ + 1/2² + 1/2³ + 1/2⁴ + ...
1/2 = 1/3¹ + 1/3² + 1/3³ + 1/3⁴ + ...
1/3 = 1/4¹ + 1/4² + 1/4³ + 1/4⁴ + ...

1/3 = (-2)⁰ + (-2)¹ + (-2)² + (-2)³ - ... = 1-2+4-8+...
1/2 = (-1)⁰ + (-1)¹ + (-1)² + (-1)³ - ... = 1-1+1-1+...
1/1 = 0⁰ + 0¹ + 0² + 0³ + ... = 1+0+0+0+...
1/0 = 1⁰ + 1¹ + 1² + 1³ + ... = 1+1+1+1+...
1/-1 = 2⁰ + 2¹ + 2² + 2³ + ...
1/-2 = 3⁰ + 3¹ + 3² + 3³ + ...
1/-3 = 4⁰ + 4¹ + 4² + 4³ + ...

Donc, si 1/0 = 1 + 1 + 1 + 1 + ..., alors nous pouvons effectuer les tables de multiplication suivantes.

1/0² = (1+1+1+1+...)²

Pièce jointe 493796

1/0³ = (1+1+1+1+...)³

Pièce jointe 493797

1/0⁴ = (1+1+1+1+...)⁴

Pièce jointe 493798

En appliquant cette méthode, je conserve l'homogénéité de la somme des valeurs dans le triangle de Pascal.

-1 = 2⁰ + 2¹ + 2² + 2³ + ... = 1 + 1 + 2 + 3 + 5 + 8 + 13 + ... = 1/0¹ + 1/0² + 1/0³ + 1/0⁴ + ...

triangle de Pascal.png

[A voir en vidéo sur Futura]

[pm42]

Ecrire un paquet de formules sans rapport avec le sujet mais avec des divisions par zéro ne va convaincre personne.

Tout cela donne l'impression que tu ne comprends pas du tout quel est le sujet.

[MissJenny]

ce qu'on sait faire c'est manipuler des "séries formelles". Par exemple, au lieu de parler de la série 0+1+2+3+... considérer la série formelle 0+x+2x^2+3x^3+... On peut manipuler ces séries (les additionner par exemple) sans se préoccuper de leur convergence, et en tirer des propriétés intéressantes. Je crois que c'est Euler qui avait inventé cette technique.

[gg0]

"d'autres arguments qui me font penser que Ramanujan s'est trompé" ?? les maths n'ont rien à faire d'une discussion de salon. On se moque de ce que pensent les autres (*) tant qu'ils ne donnent pas une preuve mathématique de leurs affirmations.
Donc AWeZiMoBu, tu n'es pas crédible, personne ne te croira. Pire, tu passes pour un rigolo !

(*) surtout quand ils ne connaissent pas les maths.

[Deedee81]

Salut,

"d'autres arguments qui me font penser que Ramanujan s'est trompé" ?? les maths n'ont rien à faire d'une discussion de salon. On se moque de ce que pensent les autres (*) tant qu'ils ne donnent pas une preuve mathématique de leurs affirmations.
Donc AWeZiMoBu, tu n'es pas crédible, personne ne te croira. Pire, tu passes pour un rigolo !
(*) surtout quand ils ne connaissent pas les maths.

On dit souvent qu'en science "une affirmation extraordinaire demande des preuves extraordinaires".
Et c'est bien le cas quand on a la prétention d'affirmer que Ramanujan (ou Hilbert, ou Poincaré, etc...) s'est trompé.
Ce n'est pas impossible, bien sûr, mais si ce n'est pas une erreur connue, vu le nombre de (grands) mathématiciens qui ont déjà examiné et/ou utilisé tout ça, on a intérêt a avoir une démonstration :
en béton armé, et respectant les règles de rigueur et de précision des mathématiques (et pas celles qu'on pourrait CROIRE être rigoureuse). Et pas juste des arguments ou des avis.
Sinon en effet on se ridiculise.

Voir aussi ce que j'ai expliqué dans l'autre discussion :
https://forums.futura-sciences.com/m...ramanujan.html

Il n'est pas rare qu'un profane se trompe totalement sur ce point (un effet DK).
Ils croient sincèrement avoir trouvé une telle erreur. Mais ils n'ont ni les compétences pour se rendre compte que c'est eux qui se trompent ni les connaissances leur permettant de voir à quel point c'est aberrant de faire ce genre d'affirmation. Mais ça ne rend pas leur affirmation vraie pour autant, évidemment.

Evidemment, tout ça se corrige avec du travail, des études, etc.... Espérons que aWeZiMoBu fait partie de ceux-là.

[SULREN]

Bonjour,

C’est dommage d’en venir à s’écharper dans un dialogue qui tourne au dialogue de sourds, alors qu’il suffit de bien préciser de quel type de sommation on parle.
- En lisant l’autre discussion qui vient d’avoir lieu sur Ramanujan et le lien que @Liet Kynes y a donné, à savoir,
https://accromath.uqam.ca/2019/01/un...a-controverse/

- Et en lisant ce que dit aussi un autre site (que je cite ci-dessous) on comprend :
« Qu’on ne parle de sommation au sens traditionnel, mais de type de sommation qui possède des propriétés qui la rende mathématiquement valide dans l’étude des séries divergentes »

Et que, par exemple, il ne faut pas lire :
1.gif
Mais:
2.gif

[gg0]

Mais ce n'est pas de cela que parle AWeZiMoBu ...

[SULREN]

Re-bonjour,

Mais ce n'est pas de cela que parle AWeZiMoBu ...

Peut-être mais c'est du "même tonneau", de la même façon d'aborder les séries divergentes.
On retrouve les deux ici: S=1+2+.....=-1/12 et S-4S=1/4

[pm42]

Sauf que la dite "approche" permet de montrer tout et n'importe quoi y compris que 0=1.

Donc si on cherche pas à en savoir plus notamment sur les sommes partielles, le rapport avec les séries, ce que Ramanujan a vraiment fait, il y a peu d'intérêt à part continuer à entretenir la confusion.

[SULREN]

Re,*

Sauf que la dite "approche" permet de montrer tout et n'importe quoi y compris que 0=1.
Donc si on cherche pas à en savoir plus notamment sur les sommes partielles, le rapport avec les séries, ce que Ramanujan a vraiment fait, il y a peu d'intérêt à part continuer à entretenir la confusion.

Tout a fait d'accord. J'ai bien vu aussi la démonstration de 0=1.
Mais je me garde de porter un jugement sur toutes ces démonstrations qui me sont contre-intuitives étant donné mon niveau limité en maths et mon incapacité à me mettre au niveau du point de vue d'un Ramanujan, et a comprendre ce qu'il a vraiment fait.

Je m'intéresse cependant vraiment à cette discussion et j'ai envie qu'elle continue parce que j'aime les maths et que j'ai envie de progresser, mais sans intervenir techniquement parce que je ne peux rien y apporter sinon (comme tu le dis) "entretenir la confusion".
Mon intervention avait juste pour but de calmer le ton des échanges afin d'éviter que le Monsieur au trigrame rouge vienne mettre fin à la discussion.

[stefjm]

@Sulren il y a pas mal de discussions sur ce thème et certaines sont très bien documentées, en particulièrement par Médiat.

[SULREN]

Re-bonjour,

@stefjm
Merci pour ton soutien dans mon envie d'approfondir ce sujet sur les travaux de Ramanujan, mathématicien que je ne connaissais et que j'ai découvert il y a quelques jours avec la discussion ouverte par Taguimdjeu. Le fait que Ramanujan soit indien a redoublé mon intérêt, pour la raison suivante:

Il y a 15 ou 20 ans, j’ai utilisé les fractions continues dans les calculs de trains d’engrenages pour mes projets d’horloges astronomiques et j’ai appris, avec surprise, que les fractions continues étaient utilisées dès le Moyen Age par les mathématiciens indiens. Puis j’ai abandonné l’usage de ces fractions parce que je me suis créé un outil bien plus performant qu’elles, dans le cadre de mes besoins s’entend,…..mais j’ai gardé de l’admiration pour elles et pour les mathématiciens indiens.

J’ai bien sûr ouvert tous les liens indiqués dans les posts (merci aux posteurs) et relu toutes les discussions sur ce sujet, dont certaines remontent à 10 ans (ce sujet est bien « un marronnier ») et j’ai apprécié les explications données par @Mediat (merci à lui).

Et cela a attisé ma curiosité pour la fonction Zeta.