Bonjour, ça fait un petit moment que je réfléchis à une contradiction dans un exercice, et je ne vois vraiment pas d'ou ça vient, surtout que ma prof nous l'a corrigé et je ne vois pas ce qui peut clocher (ça vient surement de moi mais je ne comprends pas).
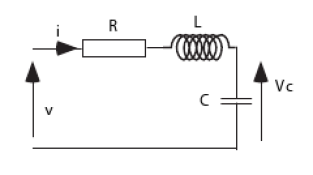
Alors, en gros on a un circuit RLC un peu modifié avec quelques interrupteurs pour compliquer le TD. On trouve les conditions initiales suivantes :
u(t=0)=0 et i(t=0)=E/R
La correction (et je comprends parfaitement) propose, pour déterminer les constantes de la solution de l'équa diff portant sur u(t) :
avec u(t=0)=0, on trouve une constante
avec i(t=0)=E/R, on dit que i(t)=C*du(t=0)/dt.
Donc du(t=0)/dt=E/CR
et on continue on trouve la deuxième constante. Mais il y a quelque chose que je comprends pas. La tangente à l’origine d'un second ordre est pourtant toujours nulle normalement ? et ici ce n'est clairement pas le cas. Du coup quand on demande de tracer, la prof avait bien dit, on trace bien une tangente à l'origine nulle. Mais la, le calcul précédent contredit ça, je ne vois pas où peut se trouver le problème.
J'espère que c'est assez clair,
Merci d'avance,
-----