RDM - Formulaire des poutres

[PPathfindeRR]

Bonjour,

Je réalise actuellement des fichiers Excel qui me permettrai de calculer toutes sortes d’éléments ou assemblages.
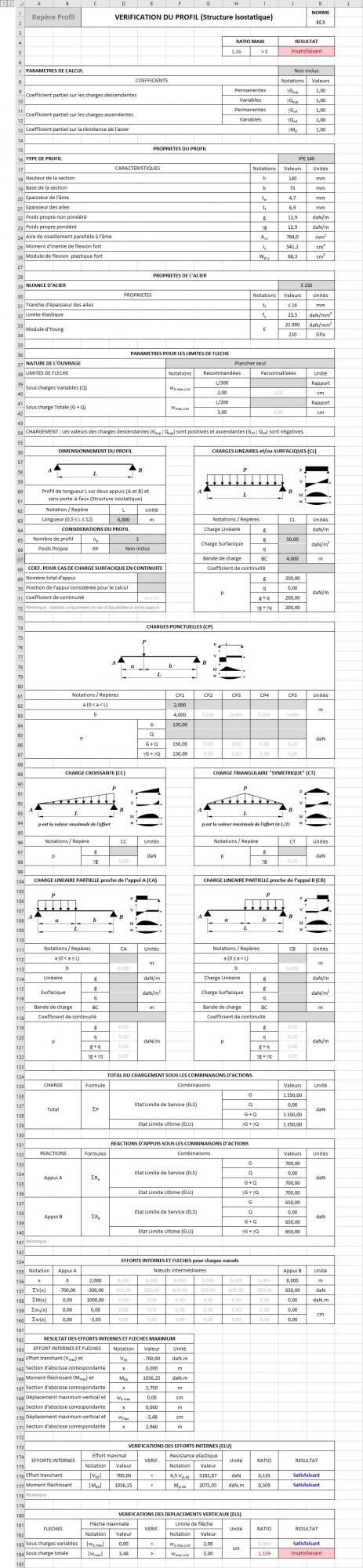
Actuellement je finalise une feuille Excel qui me calcul des poutres.

Pour calculer les efforts internes (Normal, cisaillement et moment fléchissant), je n’ai pas réussi à utiliser la méthode par tronçon (première méthode qu’on nous apprend à faire généralement) … puis la résolution des équations en travaillant par tronçon… c’est trop compliqué à réaliser avec Excel (en tous cas j’ai pas le niveau sur Excel pour ça) !

J’ai donc opté pour une méthode de superposition des efforts internes et des flèches (bien plus simple à réaliser avec Excel) … que j’ai dû entre-autre apprendre tout seul car pas appris en cours !
J’utilise pour cela les équations des cas courants des formulaires de poutre (sans porte-à-faux) qui donne l’effort pour une section d’abscisse : V(x), M(x), w(x), etc....

EXEMPLE pour le moment fléchissant (que j’applique avec ma feuille Excel) :
Une poutre (sans porte-à-faux) de 6 m sur deux appuis simples avec une charge ponctuelle à 2 m de l’appui A (distance entre appui A et charge ponctuelle noté petit a, distance entre charge ponctuelle et appui B noté petit b).

Chargement :
Charge linéaire (p) = 20 DaN/m (disons que ça correspond au poids propre de la poutre)
Charge ponctuelle (Q) = 150 daN (charge que j’applique sur la poutre)

Moment fléchissant pour charge linéaire :
M(max) = p * L^2 / 8
M(x) = p * x * (L - x) / 2

Moment fléchissant pour charge ponctuelle :
M(max) = Q * a * b / L
M(x) pour 0 < x < a = Q * b * x / L
M(x) pour a < x < L = Q * a * (1 - x / L)

Pour un tel cas (poutre chargée non symétriquement), je ne peux pas me contenter de faire la somme des efforts maximum (somme des Mmax), car après superposition, l’effort maximum résultant ne se situera pas à L/2 ni même au niveau de la charge ponctuelle ! mais quelque part entre la charge ponctuelle et L/2.

Avec Excel :
J’addition les équations donnant les valeurs de M(x) pour une section d’abscisse x donnée (x constant), et par itération, si je peux dire, (sous Excel) je détermine le x qui me donne le moment maximum ;

Le résultat avec ma feuille Excel (en appliquant la méthode de superposition ci-dessus, et me cherchant la valeur de x qui me donne la valeur maxi), j’obtiens :

RA = 192,50 daN
RB = 117,50 daN
RA + RB = 310 daN
V(x) à 2 m = 152,50 daN
V(max) = 192,50 daN à x = 0,000 m
M(x) à 2 m = 345 daN.m
M(max) = 345,16 daN.m à x = 2,125 m
W(x) à 2 m = - 2,26 m
w(max) = -2,97 cm à x = 3,761 m

Soit, Moment fléchissant maximum M(max), par superposition des M(x) à 2,125 m :
M(max) = M(2,125)
M(2,125) = (p * x * (L - x) / 2) + (Q * a * (1 - x / L))
M(2,125) = (20 * 2,125 * (8 – 2,125) / 2) + (150 * 2 * (1 – 2,125 / 8))
M(2,125) = 345,16 daN.m

Si je change la valeur de x, j’obtiens une valeur moins importante pour le moment fléchissant.
Le résultat m’a l’air correct (du moins, pas déconnant du tout) !

J’essaie maintenant d’augmenter les possibilités de ma feuille Excel, en y ajoutant d’autre type de configuration, en particulier des poutres avec porte à faux (unilatéral ou de chaque côté, de longueur différente) pour des cas de charge courants.

Mais je rencontre un petit problème concernant les formulaires de poutre (disponible un peu partout) ;
Je ne trouve pas de formulaire pour certain cas de charge avec porte-à-faux ; et c’est là que j’ai besoin de votre aide ! :

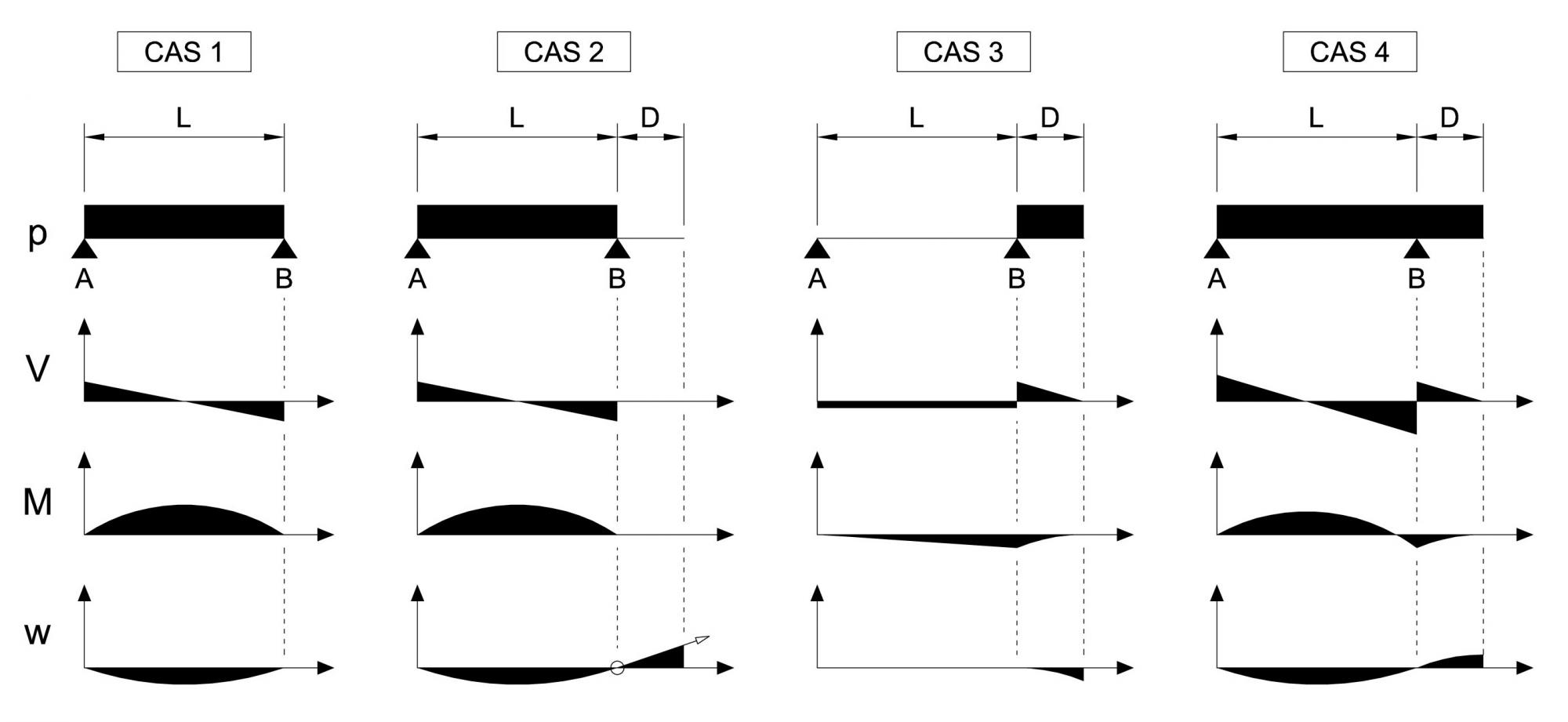
POUTRE SUR 2 APPUIS SIMPLE AVEC UN SEUL PORTE-A-FAUX

Charge ponctuelle située aléatoirement entre l’appui A et B :
V(x) = ?
M(x) = ?
w(x) = ?
Charge ponctuelle située aléatoirement sur la partie en porte-à-faux :
V(x) = ?
M(x) = ?
w(x) = ?
Charge linéaire répartie uniformément entre l’appui A et B :
V(x) = ?
M(x) = ?
w(x) = ?
Charge linéaire répartie uniformément sur la partie en porte-à-faux :
V(x) = ?
M(x) = ?
w(x) = ?
Charge linéaire répartie uniformément sur toute la longueur de la poutre :
V(x) = ?
M(x) = ?
w(x) = ?

POUTRE SUR 2 APPUIS SIMPLE AVEC 2 PORTE-A-FAUX (de longueur différente)

Charge ponctuelle située aléatoirement entre l’appui A et B :
V(x) = ?
M(x) = ?
w(x) = ?
Charge ponctuelle située aléatoirement sur la partie en porte-à-faux gauche :
V(x) = ?
M(x) = ?
w(x) = ?
Charge ponctuelle située aléatoirement sur la partie en porte-à-faux droit :
V(x) = ?
M(x) = ?
w(x) = ?
Charge linéaire répartie uniformément entre l’appui A et B :
V(x) = ?
M(x) = ?
w(x) = ?
Charge linéaire répartie uniformément sur la partie en porte-à-faux gauche :
V(x) = ?
M(x) = ?
w(x) = ?
Charge linéaire répartie uniformément sur la partie en porte-à-faux droit :
V(x) = ?
M(x) = ?
w(x) = ?

Charge linéaire répartie uniformément sur toute la longueur de la poutre :
V(x) = ?
M(x) = ?
w(x) = ?

Dernière question :
Est-ce que les équations pour les efforts donnés dans les formulaires pour une charge ponctuelle en about de porte-à-faux peut être utilisée comme une charge ponctuelle positionnée aléatoirement sur le porte-à-faux ?
Autrement dit, pouvant être superposé par exemple avec une charge linéaire qui vas au-delà de la position de la charge ponctuelle (soit utiliser une valeur pour x plus grand que L concernant la charge ponctuelle) ?

Si quelqu’un connait des formulaires de poutre contenant ces cas de figure (à moins qu’il puisse les déterminer lui-même) me rendrait un grand service !

Merci.
-----

[poffjero]

salut!
je suis egalement en train d essayer d automatiser les calculs entre excel et ma calculatrice.
pour le moment je teste les differentes possibilites de compositions de charges.
Si tu prends une poutre avec des apuis differents, tu peux couper la barre mais tu dois remplacer a la coupures pas des forces, normales et un moment. si ca t interesses on peut essayer de trouver des solutions ensembles?
Fais moi signe dans ce cas.
a plus,
jerome

[ilovir]

Bonjour

Je m'y étais essayé, il y a quelques temps.
Je l'avais fait (essayé de faire) pour un élément bois, avec les formules de l'eurocode 5

On pouvait entrer

2 charges ponctuelles (en 2 points différents), avec chacune un angle par rapport à la verticale (flexion déviée)
2 charges linéaires commençant et finissant en travée, avec angle
1 charge axiale,

Avec ça, puisqu'on est en eurocode, calcul de flèche, avec fluage et distinction de la flèche active
Avec tableau de choix des différentes classe structurales de bois (avec toutes les caractéristiques)

Heureusement, les formules bois sont relativement simples par rapport à celles en acier (en béton, je n'en parle pas)

Mais avec la flexion composée déviée avec déversement, j'ai calé bien avant la fin. Ca faisait une sacré usine à gaz.

Alors, j'ai gardé une feuille plus simple, pour les solives de plancher, et ça marche très bien.
J'en ai aussi une petite pour les assemblages cloués ou boulonnés simples. Mine de rien, c'est déjà du boulot.

J'en ai une aussi pour le calcul des poutrelles acier en flexion, avec déversement, et choix des caractéristiques des profilés dans un catalogue. Fonctionne impeccable pour les cas simples.

Pour l'acier, la solution royale reste Freelem. Il fait tout avec flambement et déversement combinés. Il y a juste à bien définir les cas de charges. Et ensuite, on change les profilés, les conditions d'appui comme on veut. Et en prime : la fréquence propre par analyse modale pour les planchers. Du coup, c'est lui que j'utilise même pour les cas simples.

Il est utilisable pour le bois, mais il faut sortir les résultats de flexion pour contrôle à la main du flambement et du déversement, puisqu'on ne peut pas appliquer au bois les méthodes de l'acier qui sont dans Freelem.

Amusez-vous bien.

[PPathfindeRR]

Bonjour,

Mon but étant de réaliser un fichier Excel (sans solveur), plus intuitif contrairement à certain logiciel de calcul RDM, signalement en rouge les éventuelles erreurs de saisie, incohérence ou résultat insatisfaisant, etc… utilisant plusieurs listes déroulantes pour limiter les erreurs de saisie (profil, etc…) qui vont chercher les données dans des sous tableaux (caractéristique du profil, formulaire de poutre, etc…).

Pour l’instant je n’ai pas trop rencontré de problème pour élaborer ma feuille Excel et les problèmes que je rencontre maintenant se situe principalement au niveau calcul RDM.
Je vais développer un peu plus mon problème.

Je vous joins un exemple et une impression écran de ma feuille Excel pour fixer des valeurs pour un cas de figure quelconque et vous exposer la méthode que j’ai utilisais (sur ma feuille Excel, les valeurs que je saisie se situe dans les cases grises) :



Une poutre (sans porte-à-faux) de longueur L = 6 m sur deux appuis simples avec une charge ponctuelle à 2 m de l’appui A (distance entre appui A et charge ponctuelle noté petit a, distance entre charge ponctuelle et appui B noté petit b).

Chargement :
Charge linéaire (p) = 200 daN/m
Charge ponctuelle (Q) = 150 daN

J’obtiens avec ma feuille Excel une réaction d’appui en A de 700 daN, une réaction d’appui en B de 650 daN et un moment fléchissant maximum de 1056,25 daN.m à x = 2,75 m (x = section d’abscisse).

(Sur ma feuille Excel j’exclus les divers coefficients de sécurité, pondérations de charge et poids propre pour simplifier le calcul).

Pour retrouver la section d’abscisse (x) qui me donne l’effort maximum sur ma feuille Excel et à l’aide des formulaires de poutre, j’ai fait des sous tableau sur mon fichier Excel qui affine le calcul, progressivement, jusqu’à obtenir une valeur au millimètre près (pour une poutre de longueur maximum de 12m).
Plus précisément, un premier tableau me donne par exemple le moment fléchissant à chaque mètre, soit un tableau de 0m à 12m (0m ; 1m ; 2m ; 3m ; 4m ; etc…).
Si l’effort maximal trouvé se situe à x = 3 m, le tableau suivant refait le même calcul pour un tableau de 2m à 4m avec plus de précision (2,0m ; 2,1m ; 2,2m ; 2,3m ; 2,4m ; etc…).
Si l’effort maximal trouvé se situe maintenant à x = 2,7 m, le tableau suivant refait le même calcul pour un tableau de 2,6m à 2,8m avec encore plus de précision (2,60m ; 2,61m ; 2,62m ; 2,63m ; 2,64m ; etc…).
Puis un dernier sous tableau encore plus précis (au millimètre près).
Et ainsi, me donnant l’effort maximum correspondant à une section d’abscisse x (au millimètre près).

En définitif, je me retrouve avec 4 sous tableau pour l’effort tranchant, 4 autres pour le moment fléchissant, 4 autres pour la flèche sous charge variable puis 4 dernier pour la flèche sous charge totale.

Je vérifie maintenant à la main le résultat (exemple : effort tranchant et moment fléchissant) que j’obtiens avec ma feuille Excel :

Je découpe ma poutre en tronçon pour étudier chaque tronçon.
Les coupures se situe à chaque nœud, soit à chaque endroit dont se situe une nouvelle application de force ou d’appui.
J’ai donc au total 3 nœuds (x = 0m, 2m et 6m), soit 2 tronçons : une de 0m à 2m (a = 2m) et une de 2m à 6m (b = 4m).

(Repère ci-dessous : X positif vers la droite, Y positif vers le haut et M positif dans le sens horaire)

MISE EN EQUILIBRE

Somme Fy = 0 ;
+ RA - (p * L) - Q + RB
+ RA - (200 * 6) - 150 + RB
+ RA + RB = + (200 * 6) + 150
+ RA + RB = + 1350 daN

Somme M/Appui A = 0 ;
+ ((p * L) * (L / 2)) + (Q * a) - (RB * L)
+ ((200 * 6) * (6 / 2)) + (150 * 2) - (RB * 6)
+ RB * 6 = + ((200 * 6) * (6 / 2)) + (150 * 2)
+ RB * 6 = + 3900
+ RB = + 3900 / 6
+ RB = + 650 daN

Déduction RA ;
+ RA + RB = + 1350 daN
+ RA + 650 = + 1350
+ RA = + 1350 - 650
+ RA = + 700 daN

Conclusion ;
RA = 700 daN
RB = 650 daN

EFFORTS INTERNES

(Le point G se situant à l’endroit de la coupure, soit un nœud qui se déplace le long de ma poutre en fonction du tronçon étudié)

1er TRONCON : 0m < x < 2m

V = Somme Fy ;
V = + RA - (p * x)

à x = 0m ;
V(0) = + 700 - (200 * 0)
V(0) = + 700 daN

à x = 2m ;
V(2) = + 700 - (200 * 2)
V(2) = + 300 daN

M = Somme M/G ;
M = + (RA * x) - ((p * x) * (x / 2))

à x = 0m ;
M(0) = + (700 * 0) - ((200 * 0) * (0 / 2))
M(0) = 0 daN.m

à x = 2m ;
M(2) = + (700 * 2) - ((200 * 2) * (2 / 2))
M(2) = + 1000 daN.m

2ème TRONCON : 2m < x < 6m

V = Somme Fy ;
V = + RA - (p * x) - Q

à x = 2m ;
V(2) = + 700 - (200 * 2) - 150
V(2) = + 150 daN

à x = 6m ;
V(6) = + 700 - (200 * 6) - 150
V(6) = - 650 daN

M = Somme M/G ;
M = + (RA * x) – ((p * x) * (x / 2)) - (Q * (x - a))

à x = 2m ;
M(2) = + (700 * 2) - ((200 * 2) * (2 / 2)) - (150 * (2 - 2))
M(2) = + 1000 daN.m

à x = 6m ;
M(6) = + (700 * 6) - ((200 * 6) * (6 / 2)) - (150 * (6 - 2))
M(6) = 0 daN.m

SUIVANT MA FEUILLE EXCEL
(Moment maximum de 1056,25 daN.m à x = 2,75m)

2ème TRONCON : 2m < x < 6m

M = Somme M/G ;
M = + (RA * x) – ((p * x) * (x / 2)) - (Q * (x - a))

à x = 2,74m ;
M(2,74) = + (700 * 2,74) - ((200 * 2,74) * (2,74 / 2)) - (150 * (2,74 - 2))
M(2,74) = + 1056,24 daN.m

à x = 2,75m ;
M(2,75) = + (700 * 2,75) - ((200 * 2,75) * (2,75 / 2)) - (150 * (2,75 - 2))
M(2,75) = + 1056,25 daN.m

à x = 2,76m ;
M(2,76) = + (700 * 2,76) - ((200 * 2,76) * (2,76 / 2)) - (150 * (2,76 - 2))
M(2,76) = + 1056,24 daN.m

A première vue, ma feuille Excel fonctionne ! la superposition des efforts obtenus grâce aux formulaires de poutre (Mx, Vx, etc…) intégré en sous tableau dans mon fichier Excel me donne le même résultat que la méthode par tronçon faite manuellement ci-dessus.

Mais comme je précisais dans mon premier message (et comme vous pouvez le constater sur mon impression écran), je suis limité à quelque cas de figure courant (ma feuille Excel est limitée à la vérification d’un profil sur 2 appuis et sans porte-à-faux, pour quelque cas de charge courant)

Et c’est là que je rencontre plusieurs problèmes si je souhaite augmenter les possibilités de mon fichier Excel :

L’idéal pour calculer toutes sortes de cas isostatiques (avec ou sans porte-à-faux) serait effectivement de procéder par la méthode des tronçons (que j’expose juste ci-dessus) au lieu d’utiliser les formulaires de poutre en superposant les efforts.
Mais dans ce cas, les calculs seront plus longs et donc le fichier Excel sera plus lourd (ce qui n’est pas génial !)
Une méthode d’ailleurs que j’ai vite abandonnée en voyant la complexité et la difficulté pour réaliser une telle feuille Excel !

De plus, avec la méthode par tronçon, je me retrouve toujours à affiner la valeur de la section d’abscisse avec des sous tableau.
A moins que l’un de vous sait comment on s’y prend pour retrouver du premier coup la section d’abscisse qui donne l’effort maximum !
Perso, je ne sais pas le faire (ni même si c’est possible) car je me retrouve avec 2 inconnues qui dépendent l’une de l’autre (la section d’abscisse et l’effort maximum).

Et dernièrement, je ne connais pas la procédure de calcul (calcul à la main) pour obtenir la flèche (autrement qu’en utilisant les formulaires de poutre) :
- Flèche pour une section d’abscisse donnée w(x)
- Flèche maximale à telle section d’abscisse w(max) à x = ?
(Ce qui m’a contraint entre-autre, et définitivement, à utiliser les formulaires de poutre pour élaborer ma feuille Excel !)

J’ai également cru comprendre que certain logiciel de RDM ne résout pas les équations mais procède de manière similaire à mon fichier Excel (ce qui me parait pas déconnant vu que ça entraine moins de calcul et allège ainsi considérablement le poids).

Voilà les raisons pour lesquelles j’utilise pour mon fichier Excel les formulaires de poutre au lieu de la méthode des tronçons et la raison de mes questions de mon premier message (si l’un de vous connais les formules, ou sait retrouver par calcul les formules pour divers cas de charge avec un et deux porte-à-faux).

[A voir en vidéo sur Futura]

[le_STI]

Salut.

Voici les simplifications qui m'ont paru évidentes (en espérant que je ne me sois pas trompé ):

POUTRE SUR 2 APPUIS SIMPLE AVEC UN SEUL PORTE-A-FAUX

Charge ponctuelle située aléatoirement entre l’appui A et B :
V(x) = identique au cas sans porte à faux, puis =0 dans la partie en porte à faux
M(x) = Idem
w(x) = Idem, puis dépend de la tangente à la poutre au point d'appui

Charge ponctuelle située aléatoirement sur la partie en porte-à-faux : équivalent au cas précédent. Il faut voir la charge comme le deuxième appui, et l'appui médian comme la charge. (petite gymnastique cérébrale)

Charge linéaire répartie uniformément entre l’appui A et B :
V(x) = identique au cas sans porte à faux, puis =0 dans la partie en porte à faux
M(x) = idem
w(x) = Idem, puis dépend de la tangente à la poutre au point d'appui

Charge linéaire répartie uniformément sur la partie en porte-à-faux :
V(x) = ?
M(x) = ?
w(x) = ?
Charge linéaire répartie uniformément sur toute la longueur de la poutre :
V(x) = ?
M(x) = ?
w(x) = ?

POUTRE SUR 2 APPUIS SIMPLE AVEC 2 PORTE-A-FAUX (de longueur différente)

Charge ponctuelle située aléatoirement entre l’appui A et B :
V(x) = identique au cas sans porte à faux, puis =0 dans la partie en porte à faux
M(x) = idem
w(x) = Idem, puis dépend de la tangente à la poutre aux points d'appui

Charge ponctuelle située aléatoirement sur la partie en porte-à-faux gauche : équivalent au cas précédent (gymnastique cérébrale)

Charge ponctuelle située aléatoirement sur la partie en porte-à-faux droit : symétrie du cas précédent

Charge linéaire répartie uniformément entre l’appui A et B :
V(x) = identique au cas sans porte à faux, puis =0 dans la partie en porte à faux
M(x) = idem
w(x) = Idem, puis dépend de la tangente à la poutre aux points d'appui

Charge linéaire répartie uniformément sur la partie en porte-à-faux gauche :
V(x) = ?
M(x) = ?
w(x) = ?
Charge linéaire répartie uniformément sur la partie en porte-à-faux droit :
V(x) = ?
M(x) = ?
w(x) = ?

Charge linéaire répartie uniformément sur toute la longueur de la poutre :
V(x) = ?
M(x) = ?
w(x) = ?

...

[ilovir]

Pour trouver un maximum avec excel, il n'y a pas d'autre moyen que de calculer tous les cas, puis d'utiliser MAX()

Par exemple 20 points sur la longueur de portée (soit tous les 30 cm, sur 6 m). Mais on peut faire bien plus si on veut

Par exemple pour le moment fléchissant, il serait calculé à chacun des ces points pour chaque cas de charge, en fonction de l'équation de ce moment le long de la poutre.

Cette équation n'est pas forcément la même tout le long.
Par exemple pour une charge P appliquée à a de l'appui de gauche, la valeur du moment en x < a est :M = P (L-a)/L * x .
Pour x > a, ça devient M = P(L-a)/L * x - P *(x-a).
Il faut donc faire des cases avec un test sur x par rapport à a, et le résultat sera à 30 cm près pour x.

Même chose pour les autres cas de charge. Pour une charge linéaire toute longueur, c'est une seule équation, mais si la charge n'est que sur une partie de la longueur, ça fait 3 équations.

Addition de tous les résultats point par point, et fonction MAX() sur ces 20 résultats récapitulatifs, avec en face le point correspondant de l'abscisse sur la portée.

Et bien évidemment, le graphique, puisqu'on a ainsi le moment fléchissant tout le long de la portée.

Si une précision de 1/20 de la portée ne suffit pas, on peut prévoir 40 ou 50 ou 100 points ; ça fait juste une feuille plus longue, mais une fois qu'elle est faite, c'est pour toujours.

On pourrait faire la même chose pour la déformée, mais là, ça devient compliqué.
Il y a une autre possibilité : puisqu'on a la valeur du moment de flexion point par point, on peut intégrer numériquement une fois, ce qui donne point par point la courbure (Moment (x) - Moment(x-L/20)) * L/20
Et quand on a point par point la courbure, on peut intégrer numériquement une deuxième fois, et on a point par point la déformée le long de la portée. Il ne reste qu'à sélectionner la valeur maxi. Graphique aussi bien sûr.

Je précise pour Path, qu'on peut très bien faire, et on y a intérêt, des sous-tableaux par exemple pour les caractéristiques des profilés acier. Fenêtre de liste qui renvoie à un tableau dans lequel on entre par la fonction Recherche.

Et bien sûr, toutes les couleurs possibles des résultats qu'on obtient, en fonction de leurs anomalies éventuelles. Et sur les graphiques aussi. Un arbre de noël, c'est de circonstance.

Et pour le solveur, puisqu'il y en a un dans excel, il peut servir à l'aide de la fonction droitereg, à écrire l'équation de la courbe des moments, ou de la déformée, à partir des points, sous forme polynomiale. L'intérêt est cependant réduit, et l'approximation pas toujours bonne. Cette équation peut apparaître toute seule sur le graphique si on choisit l'option d'une courbe de tendance avec affichage de son équation. Mais ça, ce n'est pas toujours très juste.

Bon courage, ce n'est que le début. Après, vous allez voir ...

[PPathfindeRR]

Bonjour,

@ le_STI

Merci, votre début de réponse confirme bien ce que je pensais : lorsque qu’un porte à faux n’est pas chargé, il n’affecte pas le diagramme… ça reste la même équation que pour un cas sans porte à faux (oui, c’était assez intuitif !).
Et… oui aussi, effectivement, la flèche du porte à faux non chargé dépend de la tangente à la poutre au point d'appui.

Les cas qui posent un peu plus de problème, sont les cas dont le porte à faux est justement chargé !
Et donc la grande question, comment retrouver l’équation de ces cas-ci (cas avec porte à faux chargé) ? !

Pour donner un exemple au problème, je vais exposer 4 cas
Les voici en image et avec leur diagramme (diagramme que je me représente de manière approximative… sans calcul) :



Et maintenant le calcul de ces 4 cas avec la méthode par tronçon :

Je mets chaque terme entre parenthèse pour mieux discerner les charges et les bras de levier pour m’éviter de faire des schémas (même si certaine parenthèse sont inutiles fondamentalement au calcul).

Avec X positif vers la droite, Y positif vers le haut et moment positif dans le sens horaire.

G étant le nœud qui se déplace le long de la poutre de gauche vers la droite et situé au niveau de la coupure.
x étant la distance entre le début de la poutre (situé à l’appui A) et le nœud G (situé sur la coupure).

CAS 1

POUTRE SUR 2 APPUIS SIMPLE SANS PORTE-A-FAUX
(Poutre chargée sur toute la longueur de la poutre)

Charge linéaire répartie uniformément entre appuis (p) : 100 daN/m
Distance entre appuis (L) = 6 m

MISE EN EQUILIBRE (RA et RB)

Somme Fy = 0 ;
+ RA - (p * L) + RB = 0
+ RA - (100 * 6) + RB = 0
+ RA + RB = + (100 * 6)
+ RA + RB = + 600 daN

Somme M / Appui A = 0
+ ((p * L) * (L / 2)) - (RB * L) = 0
+ ((100 * 6) * (6 / 2)) - (RB * 6) = 0
+ ((100 * 6) * (6 / 2)) = + RB * 6
+ 1800 = + RB * 6
+ RB = + 1800 / 6
+ RB = + 300 daN

Déduction de RA
+ RA + RB = + 600 daN
+ RA + 300 = + 600
+ RA = + 600 - 300
+ RA = + 300 daN

EFFORTS INTERNES (V et M)

1er TRONCON : 0 < x < 6 m

V(x) = Somme Fy = + RA - (p * x)
Pour x = 0 m ; V(0) = + 300 - (100 * 0) = + 300 daN
Pour x = 3 m ; V(3) = + 300 - (100 * 3) = 0 daN
Pour x = 6 m ; V(6) = + 300 - (100 * 6) = - 300 daN

M(x) = Somme M / G = + (RA * x) - ((p * x) * (x / 2))
Pour x = 0 m ; M(0) = + (300 * 0) - ((100 * 0) * (0 / 2)) = 0 daN.m
Pour x = 3 m ; M(3) = + (300 * 3) - ((100 * 3) * (3 / 2)) = 450 daN.m
Pour x = 6 m ; M(6) = + (300 * 6) - ((100 * 6) * (0 / 6)) = 0 daN.m

Soit avec les formulaires de poutre :

V(max) = p * L / 2
V(max) = 100 * 6 / 2 = 300 daN

V(x) = p * (L / 2 - x)
V(0) = 100 * (6 / 2 - 0) = 300 daN

M(max) = p * L^2 / 8
M(max) = 100 * 6^2 / 8 = 450 daN.m

M(x) = p * x * (L - x) / 2
M(3) = 100 * 3 * (6 - 3) / 2 = 450 daN.m

CAS 2

POUTRE SUR 2 APPUIS SIMPLE AVEC UN SEUL PORTE-A-FAUX (porte-à-faux à droite)
(Poutre chargée uniquement entre appuis A et B)

Charge linéaire répartie uniformément (p) uniquement entre appuis : 100 daN/m
Distance entre appuis (L) = 6 m
Longueur du porte-à-faux droit (D) = 2 m
Longueur totale (L + D) = 8 m

MISE EN EQUILIBRE (RA et RB)

Equations identiques au CAS 1 ;
+ RA + RB = + 600 daN
+ RB = + 300 daN
+ RA = + 300 daN

EFFORTS INTERNES (V et M)

1er TRONCON : 0 < x < 6 m

Equations identiques au CAS 1 ;
Pour x = 0 m ; V(0) = + 300 daN
Pour x = 3 m ; V(3) = 0 daN
Pour x = 6 m ; V(6) = - 300 daN

Equations identiques au CAS 1 ;
Pour x = 0 m ; M(0) = 0 daN.m
Pour x = 3 m ; M(3) = + 450 daN.m
Pour x = 6 m ; M(6) = 0 daN.m

2eme TRONCON : 6 < x < 8 m

V(x) = Somme Fy = + RA - (p * L) + RB
Pour x = 6 m ; V(6) = + 300 - (100 * 6) + 300 = 0 daN
Pour x = 7 m ; V(7) = V(6) = 0 daN
Pour x = 8 m ; V(8) = V(6) = 0 daN

M(x) = Somme M / G = + (RA * (L + (x - L))) - (p * L * ((L / 2) + (x - L))) + (RB * (x - L))
Pour x = 6 m ; M(6) = + (300 * (6 + (6 - 6))) - (100 * 6 * ((6 / 2) + (6 - 6))) + (300 * (6 - 6)) = 0 daN.m
Pour x = 7 m ; M(7) = + (300 * (6 + (7 - 6))) - (100 * 6 * ((6 / 2) + (7 - 6))) + (300 * (7 - 6)) = 0 daN.m
Pour x = 8 m ; M(8) = + (300 * (6 + (8 - 6))) - (100 * 6 * ((6 / 2) + (8 - 6))) + (300 * (8 - 6)) = 0 daN.m

CAS 3

POUTRE SUR 2 APPUIS SIMPLE AVEC UN SEUL PORTE-A-FAUX (porte-à-faux à droite)
(Poutre chargée uniquement en porte-à-faux)

Charge linéaire répartie uniformément (p) uniquement sur la partie en porte-à-faux : 100 daN/m
Distance entre appuis (L) = 6 m
Longueur du porte-à-faux droit (D) = 2 m
Longueur totale (L + D) = 8 m

MISE EN EQUILIBRE (RA et RB)

Somme Fy = 0 ;
+ RA - (p * D) + RB = 0
+ RA - (100 * 2) + RB = 0
+ RA + RB = + (100 * 2)
+ RA + RB = + 200 daN

Somme M / Appui A = 0
+ ((p * D) * (L + (D / 2))) - (RB * L) = 0
+ ((100 * 2) * (6 + (2 / 2))) - (RB * 6) = 0
+ ((100 * 2) * (6 + (2 / 2))) = + RB * 6
+ 1400 = + RB * 6
+ RB = + 1400 / 6
+ RB = + 233,33… daN

Déduction de RA
+ RA + RB = + 200 daN
+ RA + 233,33… = + 200
+ RA = + 200 - 233,33…
+ RA = - 33,33… daN

(RA négatif = Soulèvement à l’appui A)

EFFORTS INTERNES (V et M)

1er TRONCON : 0 < x < 6 m

V(x) = Somme Fy = + RA
Pour x = 0 m ; V(0) = - 33,33… daN
Pour x = 3 m ; V(3) = V(0) = - 33,33… daN
Pour x = 6 m ; V(6) = V(0) = - 33,33… daN

M(x) = Somme M / G = + (RA * x)
Pour x = 0 m ; M(0) = - (33,33… * 0) = 0 daN.m
Pour x = 3 m ; M(3) = - (33,33… * 3) = - 100 daN.m
Pour x = 6 m ; M(6) = - (33,33… * 6) = - 200 daN.m

2eme TRONCON : 6 < x < 8 m

V(x) = Somme Fy = + RA + RB - (p * (x - L))
Pour x = 6 m ; V(6) = - 33,33… + 233,33… - (100 * (6 - 6)) = + 200 daN
Pour x = 7 m ; V(7) = - 33,33… + 233,33… - (100 * (7 - 6)) = + 100 daN
Pour x = 8 m ; V(8) = - 33,33… + 233,33… - (100 * (8 - 6)) = 0 daN

M(x) = Somme M / G = + (RA * (L + (x - L))) + (RB * (x - L)) – (p * (x - L) * ((x - L) / 2))
Pour x = 6 m ; M(6) = - (33,33… * (6 + (6 - 6))) + (233,33… * (6 - 6)) - (100 * (6 - 6) * ((6 - 6) / 2)) = - 200 daN.m
Pour x = 7 m ; M(7) = - (33,33… * (6 + (7 - 6))) + (233,33… * (7 - 6)) - (100 * (7 - 6) * ((7 - 6) / 2)) = - 50 daN.m
Pour x = 8 m ; M(8) = - (33,33… * (6 + (8 - 6))) + (233,33… * (8 - 6)) - (100 * (8 - 6) * ((8 - 6) / 2)) = 0 daN.m

CAS 4

POUTRE SUR 2 APPUIS SIMPLE AVEC UN SEUL PORTE-A-FAUX (porte-à-faux à droite)
(Poutre chargée sur toute la longueur de la poutre)

Charge linéaire répartie uniformément (p) sur toute la longueur : 100 daN/m
Distance entre appuis (L) = 6 m
Longueur du porte-à-faux droit (D) = 2 m
Longueur totale (L + D) = 8 m

MISE EN EQUILIBRE (RA et RB)

Somme Fy = 0 ;
+ RA - (p * L) + RB - (p * D) = 0
+ RA - (100 * 6) + RB - (100 * 2) = 0
+ RA + RB = + (100 * 6) + (100 * 2)
+ RA + RB = + 800 daN

Somme M / Appui A = 0
+ ((p * L) * (L / 2)) - (RB * L) + ((p * D) * (L + (D / 2))) = 0
+ ((100 * 6) * (6 / 2)) - (RB * 6) + ((100 * 2) * (6 + (2 / 2))) = 0
+ ((100 * 6) * (6 / 2)) + ((100 * 2) * (6 + (2 / 2))) = + RB * 6
+ 3200 = + RB * 6
+ RB = + 3200 / 6
+ RB = + 533,33… daN

Déduction de RA
+ RA + RB = + 800 daN
+ RA + 533,33… = + 800
+ RA = + 800 - 533,33…
+ RA = + 266,66… daN

EFFORTS INTERNES (V et M)

1er TRONCON : 0 < x < 6 m

V(x) = Somme Fy = + RA - (p * x)
Pour x = 0 m ; V(0) = + 266,66… - (100 * 0) = + 266,66… daN
Pour x = 3 m ; V(3) = + 266,66… - (100 * 3) = - 33,33… daN
Pour x = 6 m ; V(6) = + 266,66… - (100 * 6) = - 333,33… daN

M(x) = Somme M / G = + (RA * x) - ((p * x) * (x / 2))
Pour x = 0 m ; M(0) = + (266,66… * 0) - ((100 * 0) * (0 / 2)) = 0 daN.m
Pour x = 3 m ; M(3) = + (266,66… * 3) - ((100 * 3) * (3 / 2)) = + 350 daN.m
Pour x = 6 m ; M(6) = + (266,66… * 6) - ((100 * 6) * (6 / 2)) = - 200 daN.m

2eme TRONCON : 6 < x < 8 m

V(x) = Somme Fy = + RA - (p * L) + RB - (p * (x - L))
Pour x = 6 m ; V(6) = + 266,66… - (100 * 6) + 533,33… - (100 * (6 - 6)) = + 200 daN
Pour x = 7 m ; V(7) = + 266,66… - (100 * 6) + 533,33… - (100 * (7 - 6)) = + 100 daN
Pour x = 8 m ; V(8) = + 266,66… - (100 * 6) + 533,33… - (100 * (8 - 6)) = 0 daN

M(x) = Somme M / G = + (RA * x) + (RB * (x - L)) - ((p * x) * (x / 2))
Pour x = 6 m ; M(6) = + (266,66… * 6) + (533,33… * (6 - 6)) - ((100 * 6) * (6 / 2)) = - 200 daN.m
Pour x = 7 m ; M(7) = + (266,66… * 7) + (533,33… * (7 - 6)) - ((100 * 7) * (7 / 2)) = - 50 daN.m
Pour x = 8 m ; M(8) = + (266,66… * 8) + (533,33… * (8 - 6)) - ((100 * 8) * (8 / 2)) = 0 daN.m

SUPERPOSITION DES CAS 2 et 3 (DONNANT LE CAS 4)

REACTIONS AUX APPUIS

RA du CAS 2 + RA du CAS 3 = RA du CAS 4
+ 300 - 33,33… = 266,66… daN

RB du CAS 2 + RB du CAS 3 = RB du CAS 4
+ 300 + 233,33… = 533,33… daN

EFFORT TRANCHANT

1er TRONCON : 0 < x < 6 m

Pour x = 0 m ; V(0) du CAS 2 + V(0) du CAS 3 = V(0) du CAS 4
Pour x = 0 m ; + 300 - 33,33… = + 266,66… daN

Pour x = 3 m ; V(3) du CAS 2 + V(3) du CAS 3 = V(3) du CAS 4
Pour x = 3 m ; 0 - 33,33… = - 33,33… daN

Pour x = 6 m ; V(6) du CAS 2 + V(6) du CAS 3 = V(6) du CAS 4
Pour x = 6 m ; - 300 - 33,33… = - 333,33… daN

2eme TRONCON : 6 < x < 8 m

Pour x = 6 m ; V(6) du CAS 2 + V(6) du CAS 3 = V(6) du CAS 4
Pour x = 6 m ; 0 + 200 = + 200 daN

Pour x = 8 m ; V(8) du CAS 2 + V(8) du CAS 3 = V(8) du CAS 4
Pour x = 8 m ; 0 + 0 = 0 daN

MOMENT FLECHISSANT

1er TRONCON : 0 < x < 6 m

Pour x = 0 m ; M(0) du CAS 2 + M(0) du CAS 3 = M(0) du CAS 4
Pour x = 0 m ; 0 + 0 = 0 daN.m

Pour x = 3 m ; M(3) du CAS 2 + M(3) du CAS 3 = M(3) du CAS 4
Pour x = 3 m ; + 450 - 100 = + 350 daN.m

Pour x = 6 m ; M(6) du CAS 2 + M(6) du CAS 3 = M(6) du CAS 4
Pour x = 6 m ; 0 - 200 = - 200 daN.m

2eme TRONCON : 6 < x < 8 m

Pour x = 6 m ; M(6) du CAS 2 + M(6) du CAS 3 = M(6) du CAS 4
Pour x = 6 m ; 0 - 200 = - 200 daN.m

Pour x = 8 m ; M(8) du CAS 2 + M(8) du CAS 3 = M(8) du CAS 4
Pour x = 8 m ; 0 + 0 = 0 daN.m

Donc lorsque j’additionne les cas 2 et 3, j’obtiens bien le cas 4.
Le cas 1 et égal au cas 2 (excepté la flèche qui se poursuit et qui dépend de la tangente à la poutre au point d'appui).

Mais comment retrouver les formules de V(x), M(x) et w(x) pour un chargement (linéaire, ponctuel, croissant, triangulaire, etc…) situé uniquement en porte à faux (comme pour le cas 3 de mon exemple) pour se passer de la méthode des tronçons (trop longue à utiliser) ?

J’ai l’impression que mon cas 3 se comporte un peu comme un encastrement… soit une poutre en console (et c’est peut-être également le cas pour tous les autres types de chargement en porte à faux, j’ai pas encore vérifier ça).

Mais si je reprends bêtement (pour l’exemple) les équations des formulaires de poutre en console (en réadaptant un peu), je retrouve les résultats de mon cas 3 pour V(x) et M(x).
A l’exception des réactions d’appui… ce qui est normal puisque dans mon cas il s’agit d’un porte à faux (poutre en continuité) et non d’une poutre en console… dans le cas d’un porte à faux, l’appui B reprend une partie de la charge située entre les appuis A et B.

(Voir formulaire de poutre en console, Page 25) :
http://www.etrussart.be/cours_isips/...s/c2060for.pdf

En me servant des formulaires de poutre dans le PDF ci-dessus, j’obtiens :

EFFORT TRANCHANT

V(x) = p * (D - (x - L))

Pour x = 6 m ; V(6) = 100 * (2 - (6 - 6))
Pour x = 6 m ; V(6) = 200 daN

Pour x = 7 m ; V(7) = 100 * (2 - (7 - 6))
Pour x = 7 m ; V(7) = 100 daN

Pour x = 8 m ; V(8) = 100 * (2 - (8 - 6))
Pour x = 8 m ; V(8) = 0 daN

MOMENT FLECHISSANT

M(x) = - p * (D - (x - L))^2 / 2

Pour x = 6 m ; M(6) = - 100 * (2 - (6 - 6))^2 / 2
Pour x = 6 m ; M(6) = - 200 daN.m

Pour x = 7 m ; M(7) = - 100 * (2 - (7 - 6))^2 / 2
Pour x = 7 m ; M(7) = - 50 daN.m

Pour x = 8 m ; M(8) = - 100 * (2 - (8 - 6))^2 / 2
Pour x = 8 m ; M(8) = 0 daN.m

Ça a l’air de fonctionner, il faut que je vérifie ça de plus près… à moins que l’un d’entre vous me confirme mon raisonnement.

[PPathfindeRR]

Oups !

CAS 1

EFFORTS INTERNES (V et M)

1er TRONCON : 0 < x < 6 m

Petite erreur de frappe pour le cas 1, il fallait lire :

Pour x = 6 m ; M(6) = + (300 * 6) - ((100 * 6) * (6 / 2)) = 0 daN.m

je précise cette erreur de frappe, mais pense que vous l'avez déjà deviné

[ilovir]

Vous allez retrouver la formule générale dans une travée : M(x) = m(x) + Mb * x/L + Ma * (1/x/L)

où Ma et Mb sont les moments sur appuis a(gauche) et b(droite), et m(x) le moment fléchissant isostatique. Pour vous Ma = 0 et Mb = pD²/2.
S'il y a une console à gauche en plus, même principe pour le Ma, et ça reste isostatique.

Si par contre il y a des travées complètes à droite ou à gauche, ça devient hyperstatique, et il faut prendre la formule des trois moments.

De même pour l'effort tranchant : T(x) = t(x) - (Mb - Ma)/L

Pour la flèche, c'est une autre paire de manches.

[PPathfindeRR]

@ ilovir

Oui, j’ai bien compris ce que vous me dite à propos d’Excel, et c’est d’ailleurs de cette manière (que vous me conseillez) dont j’ai procédé (c’était la meilleure méthode je pense aussi).
Je n’ai pas trop de problème (je pense) avec Excel (et quand je ne sais pas faire un truc, on trouve facilement des tutos sur le net)

J’ai utilisé tout un tas de sous tableau « caché » (de donnée et de résultats intermédiaires)
J’ai utilisé tout un tas de fonction (multiple SI/ET/OU imbriqués, SOMME, PRODUIT, MAX, MIN, GRANDE.VALEUR, PETITE VALEUR, RECHERCHE, EQUIV, INDEX, VALIDATION DE DONNEES pour liste déroulante, MISE EN FORME CONDITIONNELLE pour les erreurs de saisie, de résultat, valeur 0, etc…)
J’ai utilisé un maximum de liste déroulante (choix du profil, nuance d’acier, paramètres de calcul, etc…), y compris les options à inclure ou non dans le calcul (liste déroulante avec INCLUS ou NON INCLUS sélectionné)

A l’ouverture du fichier, toute les valeurs sont calculées et égales à 0 (ou valeur par défaut) en couleur gris clair.
Une valeur saisie ou un résultat autre que par défaut passe en noir.
Seul les cellules grise servent à la saisie, et les autres sont verrouillées.

Toutes les cellules sont calculées après une fonctions SI ‘’ ‘’, donc pas de résultat égal à #VALEUR! ; #DIV/0! ; ou je ne sais quoi d’autre ! toutes les valeurs sont prise en compte.
Toutes erreur de saisie sont signalées grâce aux mises en forme conditionnelles (passe en Rouge).
Tout oubli de valeur obligatoire à saisir pour la vérification me renvoie à une valeur = non vérifier (valeur texte), etc…

Mon fichier Excel fonctionne plutôt à merveille, je suis plutôt satisfait de ce premier boulot.
Je ne cherche juste à le rendre que plus puissant, avec plus d’options.

Je suis donc bien conscient du travail à accomplir et ce qui m'attend si je veux augmenter ses possibilités de calcul.
Certain dirons que je suis fou ! :
J’en suis déjà à un total de 10 000 cellules de texte et données + 15 000 cellules calculées, soit 15 000 formules… sur plusieurs lignes pour certaines d’entre-elles (total de 25 000 cellules, soit 200 lignes visibles et 800 lignes cachées par 25 colonnes de données et résultats) avec une centaine de cellule contenant une mise en forme conditionnelle pour chaque saisie ou résultat erronés, ou bien chaque valeur étant égale à 0 ou non définie car non impliqué dans le résultat final.

Oui, c’est déjà une usine à gaz ! … même pas peur !

Et je ne vous raconte pas quand ça déconnait par moment lors de l’élaboration du fichier et qu’on cherche à retrouver l’erreur (la ou les cellule(s) qui contient une erreur) dans cette usine à gaz ! il faut faire des séries de test pour identifier la cellule erronée et faire des déductions… à se claquer la tête dans le mur !!!... 3 cafés, 3 aspirines et c’est reparti !

Plusieurs petits tests rapides on bien entendu étaient fait avant de faire ce gros fichier Excel.
Ce gros fichier n’est pourtant qu’un test (un test en grandeur nature pour vérifier la faisabilité d’un futur fichier et l’exactitude des résultat finaux en comparaison avec les logiciels de calcul RDM).
Malgré qu’il fonctionne parfaitement, je dois encore revoir pas mal de chose sur l’agencement, la mise en page, et la réduction de calcul… bref, optimiser tout ça et le rendre encore plus intuitif ! pour enfin réaliser une version plus aboutie et plus performante.

Mon problème n’est donc qu’au niveau calcul RDM (pas au niveau d’Excel pour l’instant).

[ilovir]

Vous allez bientôt pouvoir proposer votre feuille en version payante ...