Phénomène des marées

[kizakoo]

Bonsoir, je travaillais un exo sur le phénomène des marées océaniques et il y'a des points que je ne saisis pas très bien:

Considérons le champ de marées C(P)= A(P)-A(T) où A désigne le champ gravitationnel créé par la lune.
Après calcul, on trouve que ce champ dérive d'un potentiel V .

1-Considérons les points où ce potentiel est extrémale , peut-on dire que la marée est extrémale aussi ? Pour le max des potentiels avons-nous une plus forte force de marée ???

2- Au point P, deux potentiels se superposent V et W celui du à la force d'attraction terrestre. On nous parle dans l'exercice de "surface terrestre isobare'' ==> on fait référence à la pression mais quelle relation entre la pression et l'attraction exercée par la terre ?? isobare = (?) égalité du potentiel V+W

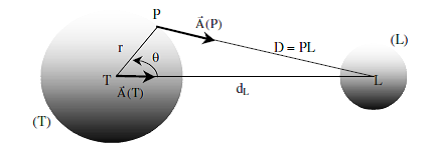
3- Enfin, pour le calcul de V le potentiel dont dérive le champ de marée. On nous demande de le faire en utilisant les coordonnées teta et r

Et là je n'ai pas su du tout par où commencer...

Je vous remercie infiniment de votre aide . J'ai vraiment besoin de vos explications pour comprendre.
Merci
-----

[LPFR]

Bonjour.
Je pense que cette façon d’aborder le problème est la plus merdique possible.
Dans la réalité, les deux corps, Terre et Lune, tournent autour de leur centre de masses commun. Sans cela ils ne pourraient rester à distance. Et sans cette rotation il n’y aurait pas de forces de marée. Il n’y aurait que le champ gravitationnel somme des deux champs, et même chose pour le potentiel.
Ignorer cette rotation est une absurdité.
Si vous additionnez bêtement les deux champs, vous aurez, autour de la Terre, un champ « décentré vers la Lune ».

La « surface isobare » est (à la fin) la surface de la mer. Une surface équipotentielle (avec le potentiel somme des deux).

Sans la rotation, (en tenant la Terre et la Lune à distance avec deux ficelles ) vous aurez une marée unique par jour.
Le maximum de marée ne coïncide pas avec le maximum du potentiel. Il y a un léger décalage du, précisément à la rotation de la Terre. C’est un tout petit décalage (quelques minutes), mais il a des conséquences surprenantes : éloignement de la Lune, ralentissement de la rotation de la Terre.

Sans la rotation, le problème est tellement absurde que je ne peux pas vous aider.

Au revoir.

[kizakoo]

Bonjour LPFR et merci d'avoir répondu. J'ai fait une petite recherche et j'ai compris que:

Un point M, de masse m, situé sur la Terre, subira dans le référentiel terrestre RT :
- son poids m ) (gravitation et force centrifuge due à la rotation de la Terre sur son axe)
- une force de marée C(P)= A(P)-A(T) où A désigne le champ gravitationnel créé par la lune resp. en un point P et au centre de la terre

le terme -mA(T) désigne la force d'inertie d'entrainement due à la rotation de la terre dans le référentiel barycentrique ayant pour origine le centre d’inertie du système Terre-Lune.


Toutefois, je n'ai pas compris une chose:

1- la terre subit une double rotation et donc on considère deux forces d'inertie d'entrainement qui se superposent. Comment s'effectue le calcul de ces deux forces?       

[LPFR]

Bonjour
Donc, si j’ai bien compris, le problème es abordé à partir du repère lié au centre de masses commun et qui tourne avec la paire (en 27 jours et quelque).
Ce repère ne tourne pas en 24 heures avec la Terre. Donc seule une accélération d’entraînement est à ajouter (celle des 27 jours).
La rotation journalière de la Terre n’est pas la responsable des marées mais uniquement du fait quelles aient lieu plusieurs fois par jour.
Donc, on l’ignore dans un premier temps.
Mais pour résoudre le problème à partir d’un repère non inertiel, il faut être masochiste en phase terminale. Je vous souhaite bien du courage. Je ne peux pas vous aider, ni veux plonger dans une méthode aussi absurde.
Au revoir.

[A voir en vidéo sur Futura]