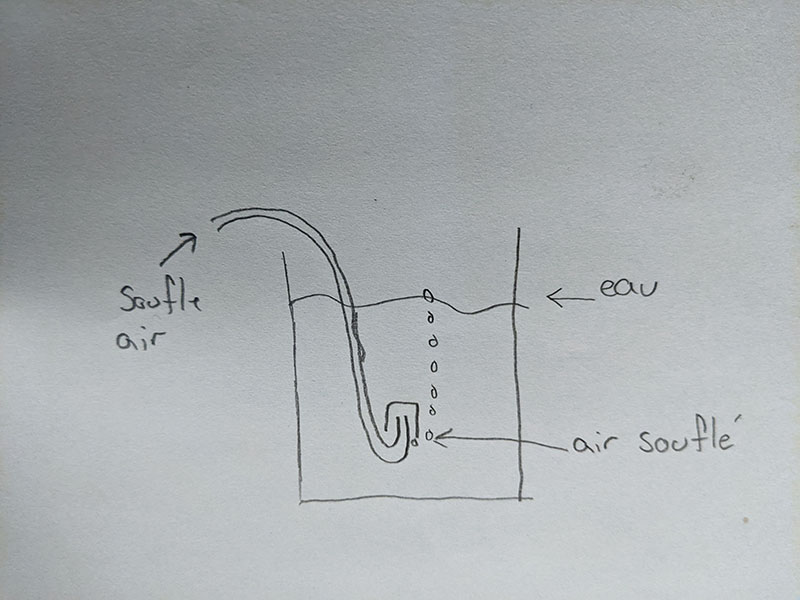
Bonjour à tous, j'aimerais savoir si on souffle de l'air dans l'eau si cet air prend de la vitesse avec la poussée d'archimède.
-----
Répondre à la discussion
Affichage des résultats 1 à 9 sur 9
Accérélation de
- 25/02/2021, 02h11 #1johny005
Accérélation de
------
-----
Qui se pose une question! Devrai toujours commencer par Wikipédia!
- 25/02/2021, 10h25 #2Deedee81
Re : Acérélation de
Salut,
Fort peu ou pas du tout, la vitesse de montée étant assez limitée (équivalent de la vitesse terminale de chute) car l'eau est un fluide assez visqueux (comparé à l'air) et surtout assez dense.
Envoyé par johny005 
https://fr.wikipedia.org/wiki/Vitesse_terminale
ou http://hmf.enseeiht.fr/travaux/beiep...xport/html/268 point 2.2.3
une fraction de mètre par seconde, la vitesse des bulles peut être plus faible que la vitesse de l'air insufflé (auquel cas on a d'assez "grosses bulles" bien entendu, le débit massique restant évidemment constant)"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
- 25/02/2021, 12h00 #3Black Jack 2
Re : Acérélation de
Bonjour,
La vitesse de remontée des bulles dépend du volume de la bulle (qui varie en cours de remontée à cause de la variation de pression hydrostatique)
La forme de la bulle en cours de montée varie avec son volume.
- forme sphérique pour bulles de diamètre < 1 mm environ
- forme elliptique pour bulles de diamètre équivalent compris dans [1 ; 15] mm
- forme en calotte sphérique pour bulles de diamètre équivalent > 15 mm
La vitesse limite est celle où les forces les frottements équilibrent la poussée d'Archimède (le poids de l'air est négligeable devant la poussée d'Archimède).
Les forces de frottement varient fortement en fonction de la forme de la bulle et le calcul de vitesse est alors plus difficile qu'on pourrait le croire.
A partir d'une certaine taille de bulles, à cause des formes variables que prend la bulle, la vitesse limite de remontée est quasi la même (environ 20 m/min)
Sur ce lien : http://ffessm67.free.fr/seminaire/20...e-Remontee.pdf
On a ceci :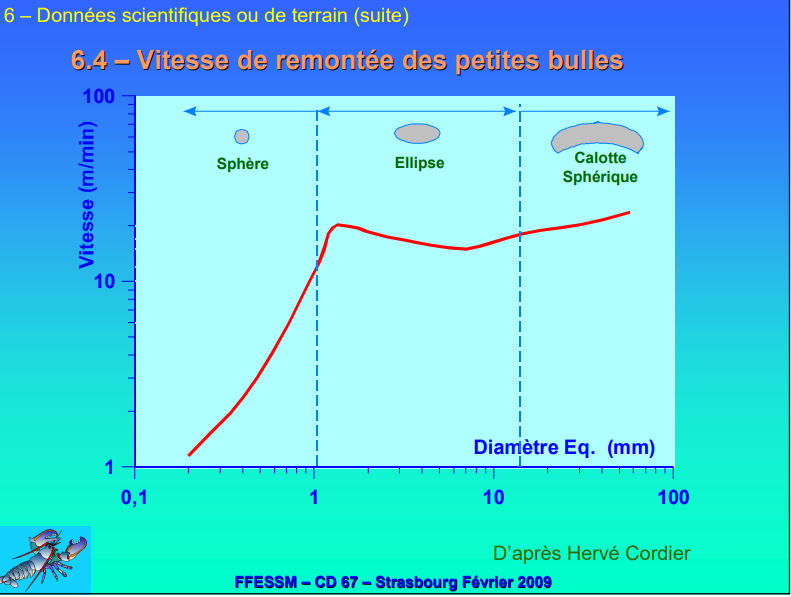
- 25/02/2021, 19h21 #4harmoniciste
Re : Acérélation de
Bonjour, Envoyé par johny005
Si tu entends par là que les bulles accélèrent jusqu'à la surface, la réponse est non:
Une vitesse limite est très vite atteinte, quand la résistance hydrodynamique liée à la vitesse de la bulle contre-balance la poussée d'archimède.Dernière modification par obi76 ; 25/02/2021 à 20h08.
- Aujourd'huiA voir en vidéo sur Futura
- 26/02/2021, 04h16 #5johny005
Re : Acérélation de
donc plus la bulle est de forme elliptique plus la pousse est grande et la friction réduit c'est bien ca?
question 2
Quand la pousser est la plus grande au plus bas ou au plus haut dans l'eau?
question 3
Comment la densité du gaz et du liquide influence t-il sur la. vitesse du gaz?Qui se pose une question! Devrai toujours commencer par Wikipédia!
- 26/02/2021, 07h17 #6obi76
Re : Acérélation de
Plus elle est de forme élliptique, plus la friction augmente. Envoyé par johny005
La poussée est la même sur toute la hauteur : elle ne dépend que du volume de la bulle (cf. Archimède) Envoyé par johny005
cf. Archimède. Vous avez le poids (qui dépend de la masse volumique de l'air), la poussée d'Archimède (qui dépend du poids du fluide déplacé donc de sa densité) et le frottement (d'autant plus grand que la bulle devient elliptique). Envoyé par johny005 Dernière modification par obi76 ; 26/02/2021 à 07h18.
\o\ \o\ Dunning-Kruger encore vainqueur ! /o/ /o/
- 26/02/2021, 10h17 #7harmoniciste
Re : Accérélation de
Lorsque la vitesse verticale atteint une certaine importance, la dépression dynamique de l'eau sur ses bords latéraux étire la bulle dans le sens de la largeur d'où la forme elliptique aplatie déjà mentionnée.
Sauf cas exceptionnel, la densité du gaz n'a quasiment aucune influence, sur la vitesse des bulles, le poids de celle ci étant négligeable devant la poussée d'Archimède (dans le rapport Densité du gaz / Densité du liquide environnant)
- 26/02/2021, 11h07 #8Black Jack 2
Re : Acérélation de
Bonjour, Envoyé par obi76
Attention que le volume de la bulle augmente en cours de remontée puisque la pression hydrostatique diminue. (supposé à température constante)
Si l'expérience est dans un verre (comme cela semble représenté), l'effet de la variation de volume d'une bulle en cours de remontée sera négligeable.Dernière modification par Black Jack 2 ; 26/02/2021 à 11h08.
- 26/02/2021, 11h42 #9obi76
Re : Acérélation de
Vu le schéma ça ne m'avait pas paru utile de le préciser vu la hauteur, mais effectivement si la hauteur n'est plus négligeable, ça changera oui Envoyé par Black Jack 2 
\o\ \o\ Dunning-Kruger encore vainqueur ! /o/ /o/