C'est encore moi
Je tombe maintenant sur un truc un peu délicat...
Je me retrouve à étudier la quantité suivante (j'étudie ça malheureusement numériquement, c'est pas analytique) :
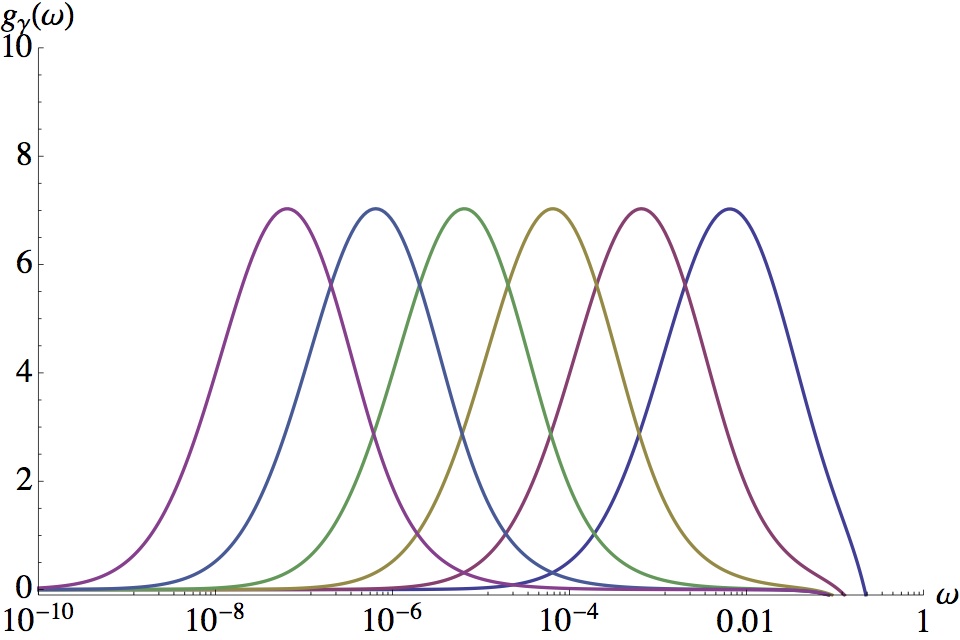
. En fonction du paramètre gamma qui tend vers 0, cette intégrale tend vers f(0). Bon, je me dis que mes fonctions g_gamma(x) tendent vers un delta et ça y ressemble effectivement (quand je trace, c'est effectivement un pic qui devient de plus en plus étroit et de plus en plus haut).
Le problème est que je sais par une autre méthode que l'intégrale ci-dessus, pour gamma exactement égal à 0, ne vaut pas f(0). Il y a bel et bien une discontinuité car mes fonctions g_gamma(x) dependent d'une quantité, appelons la, que je sais être délicate dans le sens où :
Comment concilier cette discontinuité dans la valeur de mon intégrale avec une fonction delta ? Suis-je ici dans un cas où la théorie des distributions ne peut pas être appliquée ?
Merci d'avance
-----