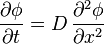Bonjour,
Je me pose deux questions bêtes à propos de la solution de l'équation de d'Alembert (Equation des ondes) en une dimension
dont la solution est en
D'où, deux questions :
1 Comment faire pour trouver cette solution sans savoir (et parachuter) le changement de variable magique kivabien? (h=ct-x et g=ct+x)
Pour l'instant, la seule solution honnête que j'ai trouvée (ie sans connaitre à l'avance le truc) est de transformer par Laplace la partie temporelle (t), par Fourier la partie spatiale (x), de trouver formellement la solution, puis de revenir aux originaux de Laplace, et de Fourier.
2 Comment se transforme un Laplacien (par rapport à l'espace) par une transformation de Laplace (temporel) ?
Merci d'avance.
-----