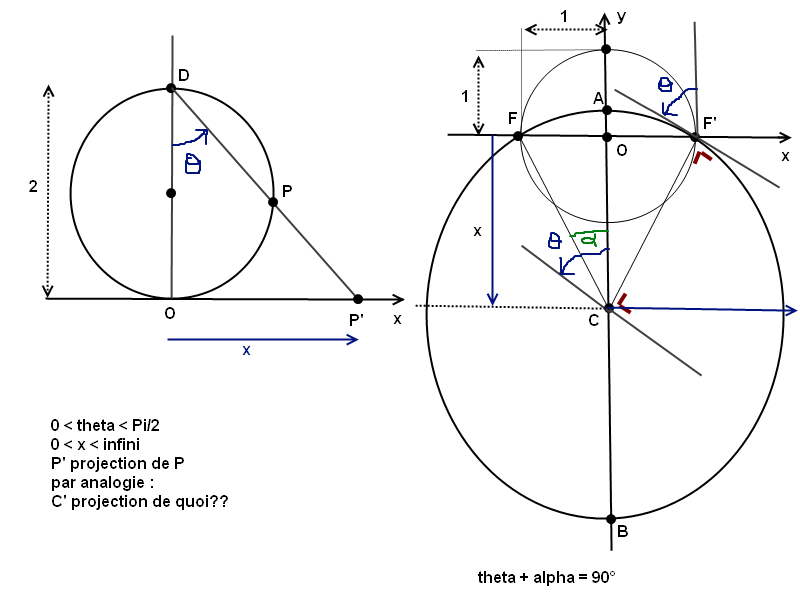
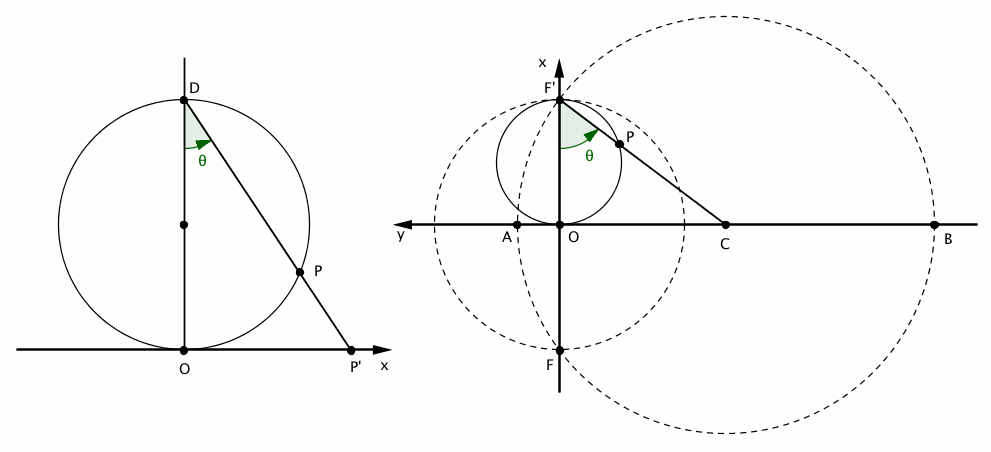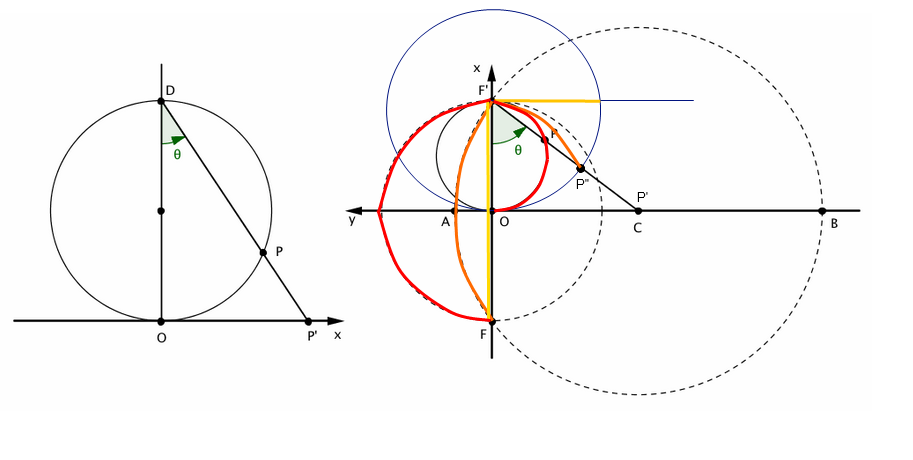Si M est un point du cercle, la droite (BM) coupe la droite (FF') au point M' de coordonnées (0,t).
La droite (BM'), a pour équation : q'y+tx=q't, c'est-à-dire : y-qtx=t.
On détermine M comme intersection de cette droite et du cercle : on obtient une équation du second degré qui fournit les deux points d'intersection, mais comme on connaît une des solutions, le point B, l'autre, le point M, est facile à obtenir.
-----



 à laquelle se trouve:
à laquelle se trouve: