Bonjour
J'essaye de comprendre la contraction des longueurs et la dilatation du temps dans la relativité restreinte.
Après avoir un peu trituré les formules, j'ai essayé de me faire un shéma pour tenter de mieux comprendre ces deux phénomènes
Merci de me dire où je pêche dans mon raisonnnement ce qui est probablement le cas quelque part.
en triturant un peu les équations de la relativité restreinte et en remplaçantet
par les valeurs avec
et
adéquates
on peut les réécrire facilement ainsi :

J'ai commencé par la contraction des longueurs avec l'équation, (1) pour ce faire on poseet
pour dire que tous les évènements se passent au même instant

que l'on peut écrire
Description des évènements du schéma :
Soit deux référentiels orthonormés identiqueset
, lorsqu'ils sont au repos sont
tels que unité de temps = 1 et unité de longueur = 1
on définivitesse de la lumière constante
constante dans
et
. on a alors une diagonale



on place dans le référentielune règle de longueur = 1 unité de longueur et on anime le référentiel
d'une vitesse rectiligne
par rapport au réfentiel R'
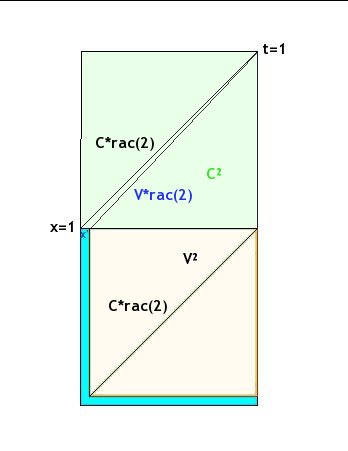
Le référentielest représenté dans le schéma par le carré

Sa longueur propre = 1 est assurée par la constante(je me sers du référentiel orthonomé pour représenter le carré
dans le même schéma, mais les unités de dimension sont différentes)
De la même manière on représente le carrédans le référentiel
au repos (fixe)
Dans le référentiella distance entre deux observateurs fixes qui observent au même instant
la longueur propre = 1 du référentiel
en mouvement sera
selon l'équation (2)
est la suface en bleu
est la racine carré de cette surface
à des vitesses non relativites la surface bleuesera proche de 1
=>
. la contraction des longueurs sera de .5 pour mille
à des vitesses relativistes la surface bleuesera proche de 0
=>
mesuré dans le repère fixe
, pour une longueur propre égale à 1, soit une longueur visible dans
contractée 100 fois
Merci d'avance pour vos rectifications et compléments
schéma en pièce jointe au cas où le serveur qui héberge l'image ferait défaut
-----




 Irruption d'une notion de temps absolu dans un raisonnement sur la RR...
Irruption d'une notion de temps absolu dans un raisonnement sur la RR...
 Cela ne correspond pas à l'usage normal du concept de référentiel. Deux référentiels distincts et inertiels sont en mouvement uniforme l'un par rapport à l'autre, il ne peut y avoir de changement d'état de mouvement.
Cela ne correspond pas à l'usage normal du concept de référentiel. Deux référentiels distincts et inertiels sont en mouvement uniforme l'un par rapport à l'autre, il ne peut y avoir de changement d'état de mouvement.
 autrement dit pour le cas trivial c'est le cas où la vitesse relative en R et R' est zéro ? c'est bien ça ? ...c'est ce que j'essayais d'exprimer en parlant de deux référentiels identiques.
autrement dit pour le cas trivial c'est le cas où la vitesse relative en R et R' est zéro ? c'est bien ça ? ...c'est ce que j'essayais d'exprimer en parlant de deux référentiels identiques.
