Principe de wolfgang rindler

[Zefram Cochrane]

Bonjour,
je voudrais savoir si ma façon d'appliquer ce principe (https://kampungpadi.files.wordpress....relativity.pdf p47) est correcte?

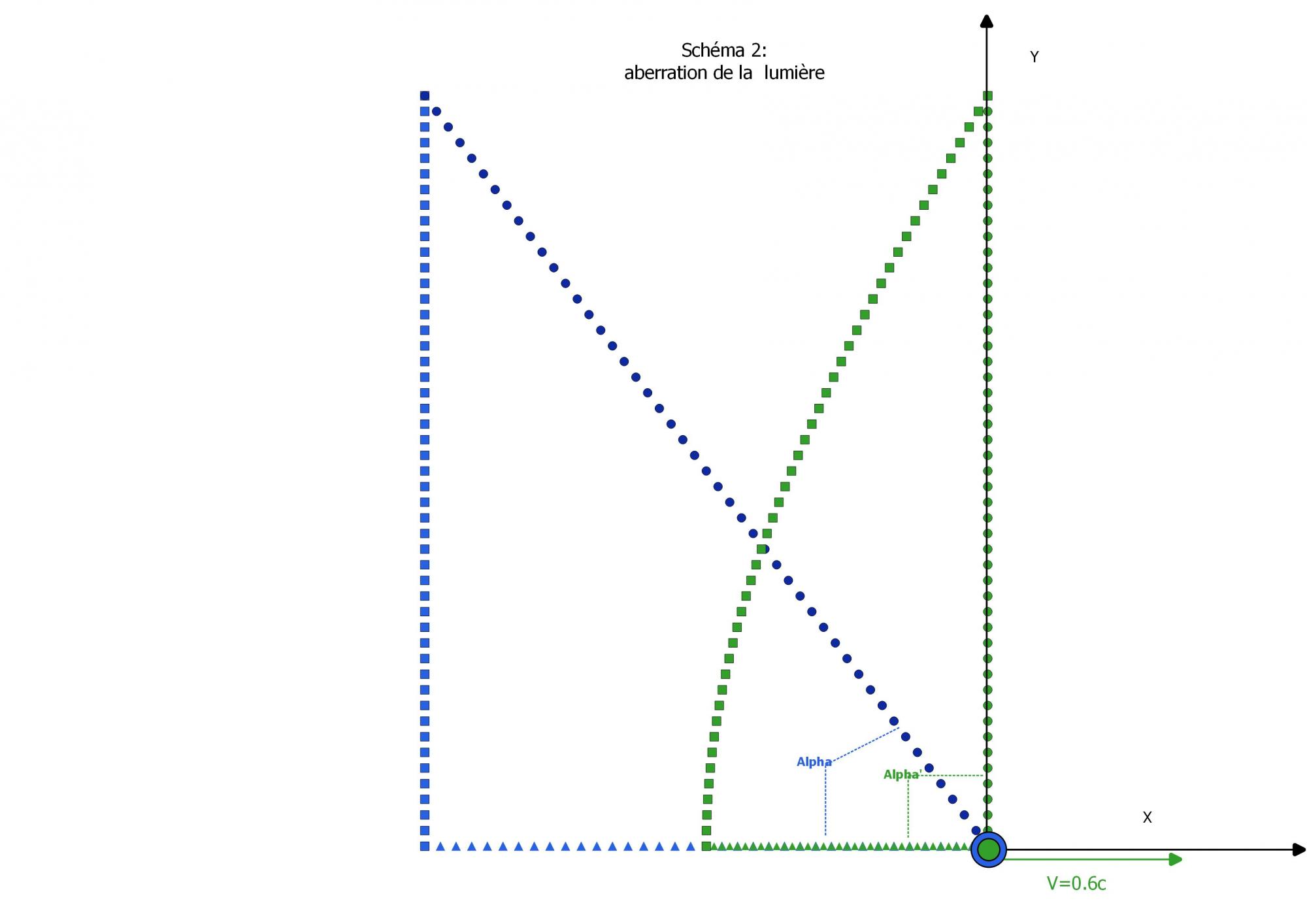
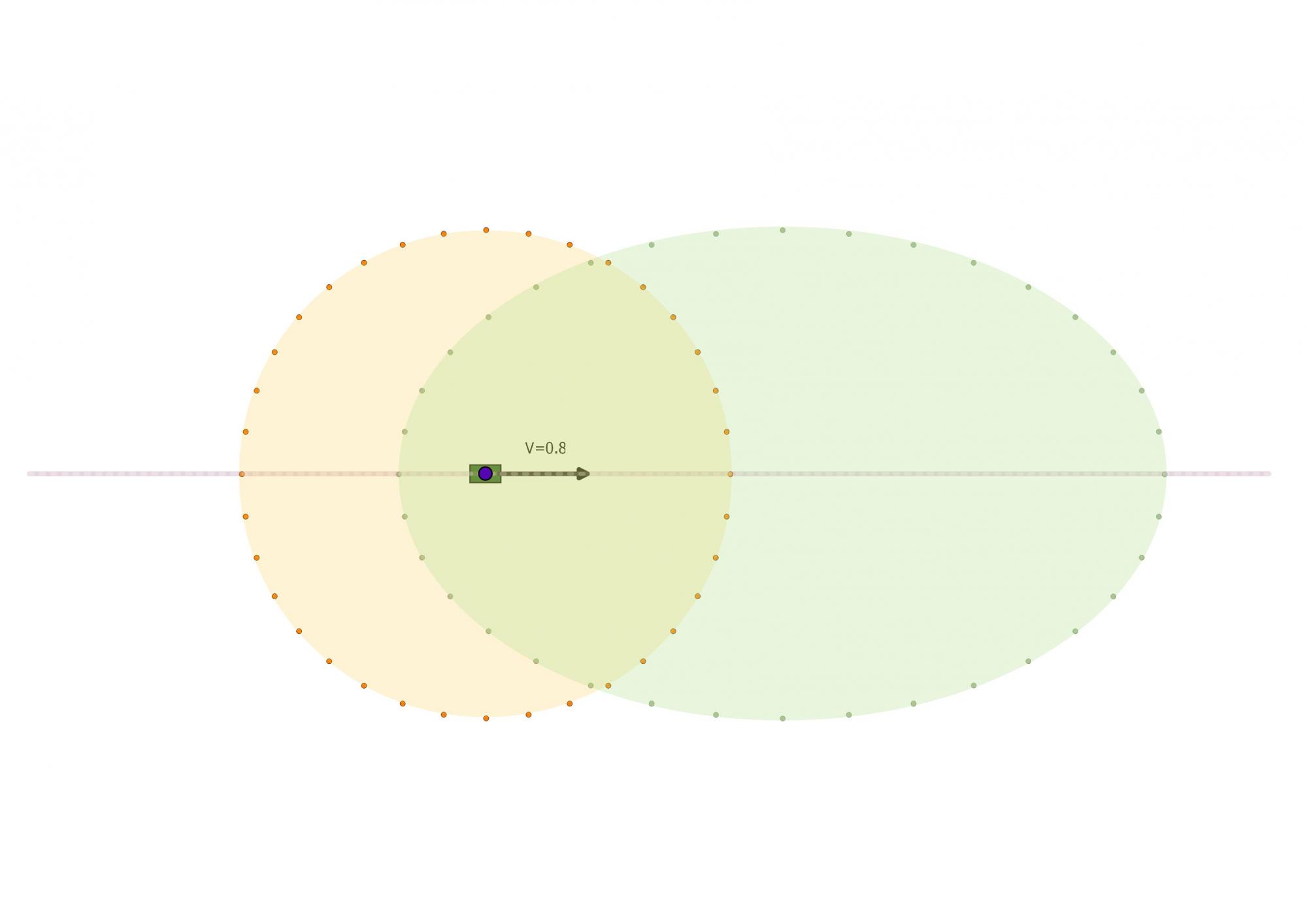
Pour calculer la perspective qu'aurait un observateur Mobile de son environnement (paysage) avec une vitesse relative V suivant l'axe des X par rapport au paysage j'ai une technique que j'ai appelé effet de perspective (qui combine l'effet Doppler et l'effet d'aberration).

Connaissant les coordonnées Xp et Yp d'un point par rapport à un observateur Stationnaire coincidant avec le Mobile .dans le paysage et donc la distance j'utilise les Tls de la manière suivante :


avec Yp'=Yp on vérifie que

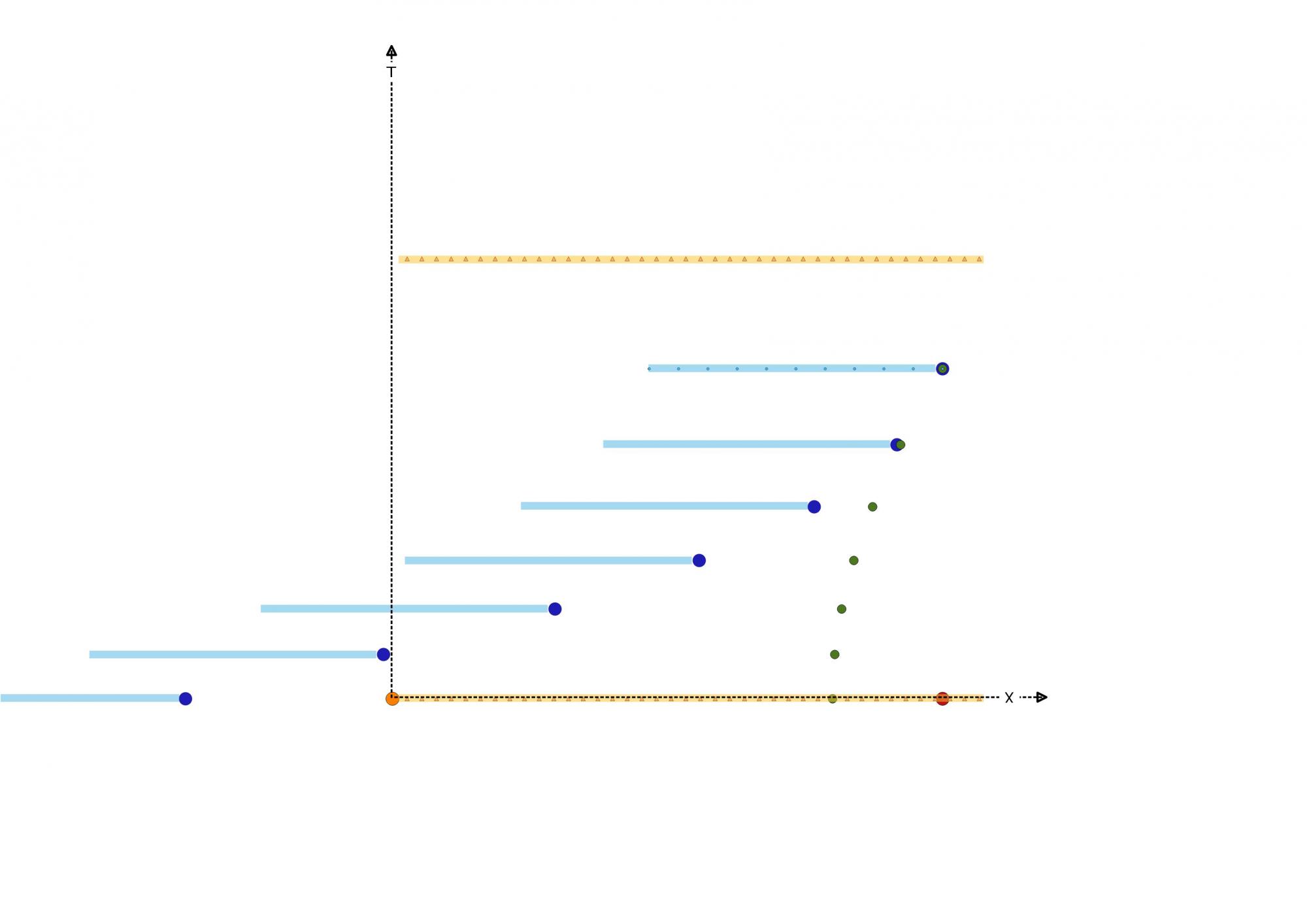
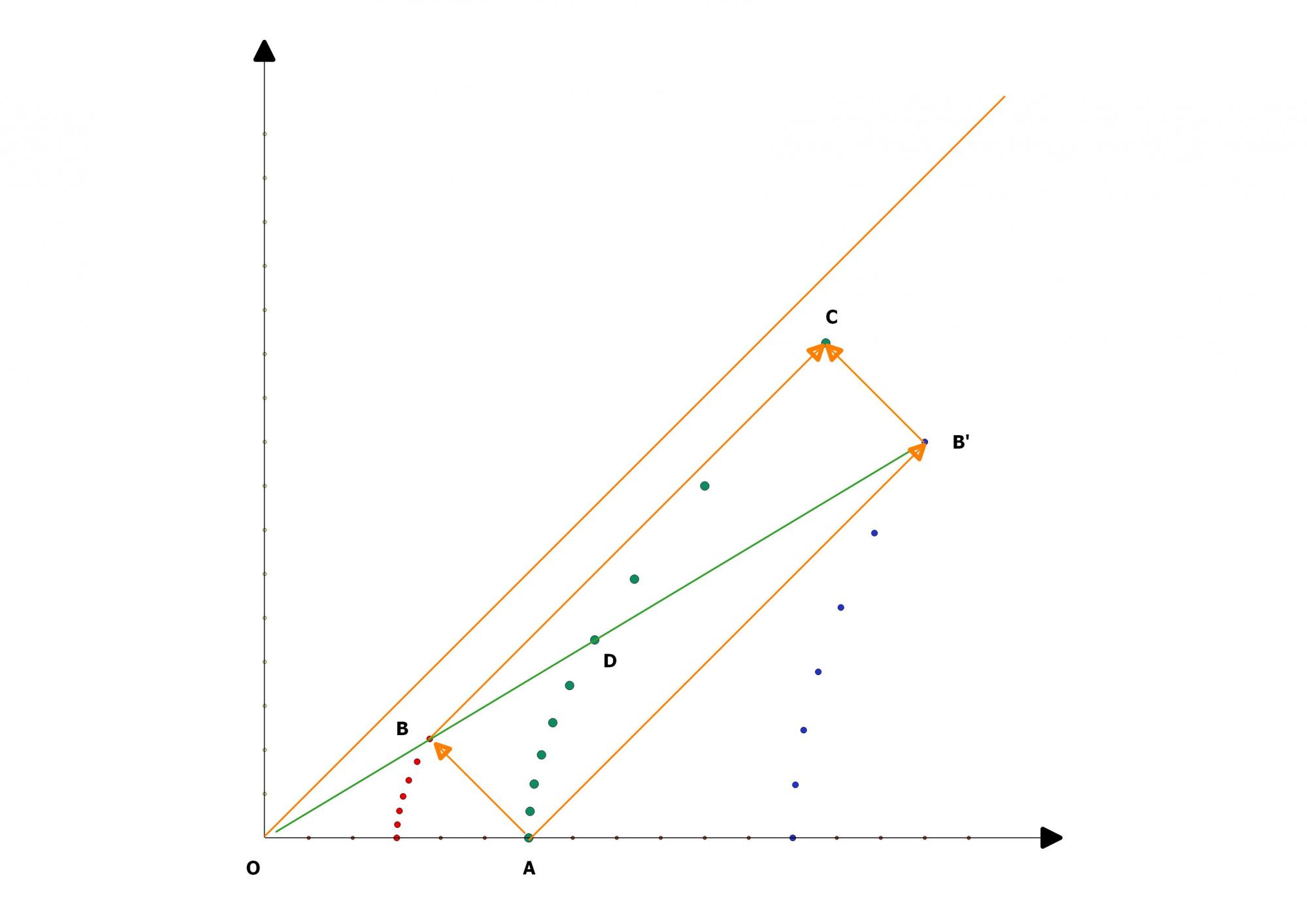
Cela me donne pour l'expérience de la lanterne du mât du bâteau la perspective de Vert (Mobile), le mousse au pied du mât par rapport à Bleu (Stationnaire), le naufragé sur une île déserte.

Sachant qu'il n'y a que dans les référentiels inertiels ou la longueur coordonnée Sp (mesurée par échange de signaux lumineux) s'éparant P de l'observateur correspond à la longueur propre Sp° mesurée avec une règle graduée,

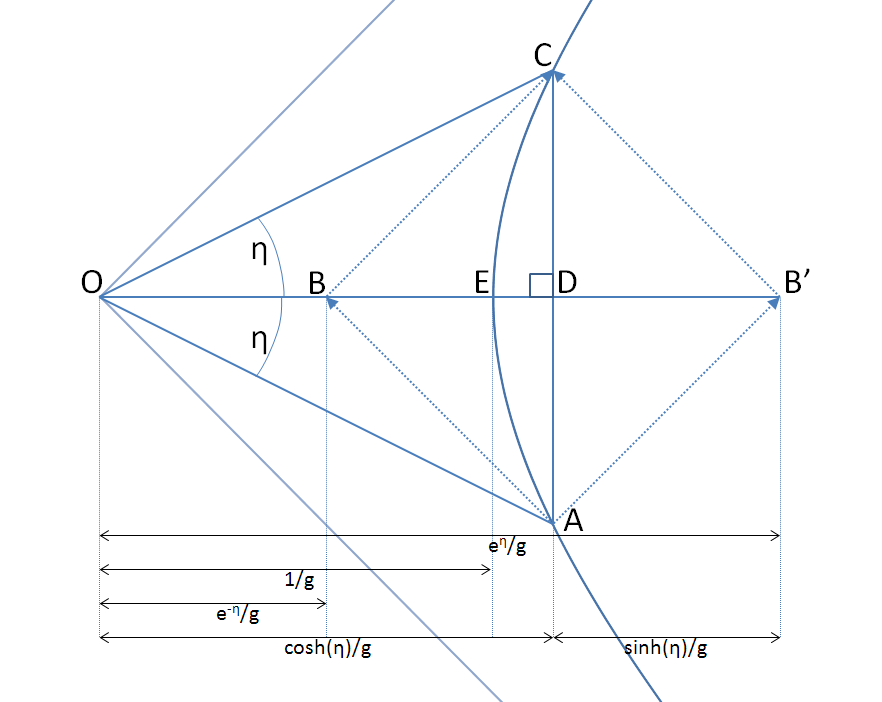
La question est qu'elle est la perspective du Voyageur, ORANGE, qui accélère continuement depuis la base d'un phare et coincide avec Vert et Bleu tout en étant comobile avec Vert.

Par application du principe de Rindler, j'affirme qu'il aura la même perspective que Vert, mais que n'étant pas inertiel la distance coordonnée Sp' ne correspondra pas avec la longueur propre Sp°' ie la longueur d'une règle , liée au Voyageur et dont l'autre extrémité coinciderait avec le point P au moment de l'observation (par le Voyageur).

Mon affirmation est-elle correcte selon vous?
-----

[mach3]

pas encore lu ce qui précède, mais je donne une réponse à la question dans l'autre fil qu'il est inutile de hors-sujettiser plus :

Salut Mach 3 .
As tu des références pour les coordonnées de Lass?
j'ouvre un sujet dessus.

https://en.wikipedia.org/wiki/Rindle...ation_formulas

regarder dans le tableau "Radar coordinates (Lass coordinates)"

m@ch3

[Zefram Cochrane]

Ma question est comment décrire les coordonnées de Lass? A quoi serve-t'elles ? que dois-je comprendre dans radar coordinates?
Par exemple pour Rindler
Soit Orange une station Vert situé à : à T=0s. à T=0s, Vert accélère avec une accélération propre
d'où Rh = 30 000 000s.l
à Vert se trouvera à une distance de Orange.
la vitesse atteinte sera alors : -> ->

Dans les coordonnées de Lass :
et vu la formule on peut penser que X et T correspondent aux X et T des coordonnées de Rindler.
Dans la formule X et T des coordonnée de Lass on a


comment interpréter x et ?

[mach3]

Note : j'ai omis les flèches de vecteur sur les bipoints.

On considère un immobile de Rindler. Il est tel que si M est un évènement de sa ligne d'univers, alors il existe un évènement O tel que . En géométrie euclidienne, ceci est la description d'un cercle, mais ici, nous sommes en géométrie minkowskienne et on décrit alors une hyperbole.

En géométrie euclidienne, si je prends deux points A et B du cercle de centre O, si j'ai , la corde AB mesure , l'arc AB mesure .

En géométrie de minkowski, c'est très similaire, pour deux évènements A et B de l'hyperbole de foyer O, si , la corde AB mesure et l'arc AB mesure

La longueur de l'arc est, en géométrie de Minkowski, la durée propre de l'arc.

Une distance radar se mesure par l'aller-retour d'un signal de genre nul d'un observateur vers un évènement (généralement un point de la ligne d'univers d'un objet). Le protocole est simple, l'observateur enclenche son chrono quand il envoie le signal et l'arrête quand il reçoit le signal retour. Il divise la durée en secondes par deux, cela donne la "distance radar" à l'évènement en seconde-lumière.

Quand l'évènement mesuré est un point d'un objet immobile par rapport à l'observateur et que l'observateur est en mouvement relatif uniforme, cette distance radar est sans ambiguité dans un interprétation à la sauce physique classique : si la lumière à mis deux secondes pour faire l'aller-retour, alors elle a parcouru 600 000 km, donc l'objet est à 300 000 km.

Quand l'objet bouge (l'observateur étant toujours en mouvement rectiligne uniforme), c'est légèrement plus délicat. A la sauce classique c'est "j'ai reçu à 0h45m10s le signal retour alors que je l'ai envoyé à 0h45m4s, j'en déduis donc qu'à 0h45m7s, l'objet était à 900 000 km". Géométriquement, on impose que la distance radar soit la longueur d'un vecteur orthogonal à la ligne d'univers de l'observateur, joignant cette ligne d'univers et l'évènement mesuré.

Soit A l'évènement de départ, B l'évènement mesuré, C l'évènement d'arrivée, on construit l'évènement D sur le segment AC tel que BD.AC=0 (c'est le projeté orthogonal de B sur la droite (AC). on a :
AB^2=BC^2=0 (segments de genre nuls)
AB^2=(AD+DB)^2=AD^2+DB^2+2AD.D B=AD^2+DB^2=0 et pareillement
BC^2=BD^2+DC^2=0
AD, DC et DB ont donc la même norme, AD et DC étant de genre temps et DB de genre espace. La durée AC, divisée par 2 donne la durée AD (ou DB) qui correspond à la longueur BD (au facteur c près).

Quand l'observateur n'est pas en mouvement rectiligne uniforme, là c'est vraiment plus délicat. Reprenons le cas précédent : l'observateur ne suit plus la droite entre les évènements A et C. Il passe par ces évènements (c'est toujours lui qui envoie le signal puis le réceptionne le signal réfléchi), mais pas nécessairement par l'évènement D. La distance radar, qui donne la longueur propre de DB peut ne correspondre avec aucune longueur propre prise entre B et un évènement de la ligne d'univers de l'observateur.
En particulier, un immobile de Rindler voit ses mesures de distance radar "faussées", et ce d'autant plus que la durée entre A et C est longue. En gros on doit avoir (la corde à peu près égale à l'arc) pour que la distance radar ne soit pas trop faussée.

La suite plus tard...

m@ch3

[A voir en vidéo sur Futura]

[Mailou75]

Salut,

(...) j'ai une technique que j'ai appelé effet de perspective (qui combine l'effet Doppler et l'effet d'aberration).

Aberration et Doppler c'est kif kif, sauf que l'apellation Doppler est reductrice car limitée a une direction radiale. Et la perspective c'est autre chose (/autocensure)... Juste change de terme, que penses tu de "retro-spective" ?

Par application du principe de Rindler, j'affirme qu'il aura la même perspective que Vert, mais que n'étant pas inertiel la distance coordonnée Sp' ne correspondra pas avec la longueur propre Sp°' ie la longueur d'une règle , liée au Voyageur et dont l'autre extrémité coinciderait avec le point P au moment de l'observation (par le Voyageur).

Mon affirmation est-elle correcte selon vous?

Non. De maniere infinitesimale le voyageur acceleré (orange ?) est inertiel et identique a vert (? celui qui a la meme vitesse au meme evenement). Ils voient donc exactement la meme chose. Voir le fil que tu sais... où on montre un changement de repere possible en chaque point de la trajectoire de l'acceleré. La difference c'est que l'acceleré a un horizon (de Rindler), ce qui signifie juste que si il continue d'accelerer il ne verra jamais certains evenements, alors que celui en MRU les verra un jour, mais pas a ce moment là

A+

[Zefram Cochrane]

Salut,

Aberration et Doppler c'est kif kif, sauf que l'apellation Doppler est reductrice car limitée a une direction radiale. Et la perspective c'est autre chose (/autocensure)... Juste change de terme, que penses tu de "retro-spective" ?

je sais bien que c'est kif kif : Certain diraient que l'effet Dopller comprend l'aberration d'autre l'inverse. Comme je parle de perspective, il ne m'a pas semblé idiot de parler d'effet de perspective; après si certains préfèrent aberration ou le Doppler pour parler de transposition de perspective d'un observateur à celle d'un autre, je ne vais pas m'acharner la dessus.

Non. De maniere infinitesimale le voyageur acceleré (orange ?) est inertiel et identique a vert (? celui qui a la meme vitesse au meme evenement). Ils voient donc exactement la meme chose.

Non...mais on est d'accord
C'est comme ça que j'entend appliquer le principe de Rindler. tu vois ce que perçoit un observateur du paysage, comme d'après le principe de Rindler,si je l'applique correctement ce qui est la question, un accéléré verra la même chose qu'un comobile en MRU par rapport au paysage, je peux donc utiliser les TLs pour trouver ce que voit l'accéléré

Voir le fil que tu sais... où on montre un changement de repere possible en chaque point de la trajectoire de l'acceleré. La difference c'est que l'acceleré a un horizon (de Rindler), ce qui signifie juste que si il continue d'accelerer il ne verra jamais certains evenements, alors que celui en MRU les verra un jour, mais pas a ce moment là

il n'y a pas de soucis là dessus non plus

[Zefram Cochrane]

Quand l'évènement mesuré est un point d'un objet immobile par rapport à l'observateur et que l'observateur est en mouvement relatif uniforme, cette distance radar est sans ambiguité dans un interprétation à la sauce physique classique : si la lumière à mis deux secondes pour faire l'aller-retour, alors elle a parcouru 600 000 km, donc l'objet est à 300 000 km.

J'attendrai la suite pour me faire une opinion définitive.
Pour un MRU, il n'y a pas de soucis.
Si Vert se trouve à T=0s à Rh=30 000 000s.l de Orange et qu'il s'éloigne de Orange avec une accélération propre de g°=10m/s²,
alors, si à T=0s(où il voit Orange tel qu'il était à T=-30 000 000s) il envoie un signal radar sur Orange, jamais il n'en recevra l'écho puisque le signal atteindra Orange à T=30 000 000s et que Vert ne verra jamais Orange à T=0s.Donc cela voudrait dire que la distance apparente est oo si elle devait correspondre à la distance radar/2.

Lorsque Vert atteint la vitesse V=0.6c, il se trouve à une distance So=37 500 000s.l de Orange à T=22 500 000s; il voit donc Orange tel qu'il était à T=-15 000 000s.l mais à une distance X de 37 500 000s.l ( repère inertiel d'Orange). La question est qu'elle est la distance coordonnée dans son propre repère voit il Orange à T=-15 000 000s? est-ce So'= So/2= 18 750 000s.l?
Pour la distance propre c'est 30 000 000s.l.

Cordialement,
Zefram

[invite6c093f92]

Je profites d'avoir une connexion pour poser ça:

http://www.phys.ens.fr/IMG/pdf/docRG.pdf
A partir du chapitre 6 p 24.

[Zefram Cochrane]

Merci Didier pour la référence. Il faudra que je la potasse pour décrypter ce qui est dit dans la section consâcrée à Rindler.

moi voici comment je calcule la distance radar:
Soit Vert un observateur situé à Rh=30 000 000 de Orange une station. A T=0s, Vert s'éloigne de Orange en accélérant avec une accélération propre de g°=10m/s². A T=0s il envoie un signal radar.
Soit Rouge situé à Rq=15 000 000s.l de Orange et qui accélère à q°=20m/s²
Soit Bleu situé à Rp= 60 000 000s.l de Orange et qui accélère à p° = 5m/s².

Signal radar réféléchi par Rouge.
lorsque Rouge percevra le signal, il se trouvera à Xq=Rq*Cosh(u°) à l'instant Tq=Rq*Sinh(u°).
Je peux écrire que Rq*Cosh(v°) = Rh - T avec T=Tq -> Rq*[Cosh(u°) + Sinh(u°)] = Rh -> [EXP(u°)] =2 -> U=0.6c

A Tq en Xq, Rouge réfléchit le signal il atteindra Vert à l'instant Tv = Rh*Sinh(v°) en Xv=Rh*Cosh(v°).
Je peux écrire que Rq*Cosh(u°) + (Rh*Sinh(v°) - Rq*Sinh(v°)) = Rh*Cosh(v°)
Rq/[Exp(u°)]=Rh/[Exp(v°)] -> [Exp(v°)] = [Exp(u°)]*Rh/Rq = [Exp(2*u°)] donc Vert recevra l'écho radar au bout d'une durée propre de Tv°' = 4 158 883s ce qui fait une distance radar de Tv°'/2=2 079 441.5s.l

Si on fait la même chose avec Bleu on retrouve les même valeurs de u° et v°.
Quand j'avais fait le calcul je n'en avais pas déduit que Vert verrait Rouge et Bleu a une distance apparente coordonnée équidistante de Tv°'/2 mais que Vert verrait Rouge redschifté d'un facteur 2 et Bleu blueschifté d'un facteur 2.

Cordialement,
Zefram

[Mailou75]

je sais bien que c'est kif kif

Non...mais on est d'accord

il n'y a pas de soucis là dessus non plus

Alors tout va bien

Bonne journée a vous

[mach3]

Désolé pour l'attente, compliqué d'avoir du temps en ce moment...

Je reprends, mais juste quelques précisions sur ce que j'ai dit avant :

Note : j'ai omis les flèches de vecteur sur les bipoints.

On considère un immobile de Rindler. Il est tel que si M est un évènement de sa ligne d'univers, alors il existe un évènement O tel que . En géométrie euclidienne, ceci est la description d'un cercle, mais ici, nous sommes en géométrie minkowskienne et on décrit alors une hyperbole.

En géométrie euclidienne, si je prends deux points A et B du cercle de centre O, si j'ai , la corde AB mesure , l'arc AB mesure .

En géométrie de minkowski, c'est très similaire, pour deux évènements A et B de l'hyperbole de foyer O, si , la corde AB mesure et l'arc AB mesure

La longueur de l'arc est, en géométrie de Minkowski, la durée propre de l'arc.

c'est implicite, mais mérite d'être mentionné, on est ici restreint à 2D en euclidien ou 1+1D en minkowskien.

Donc, maintenant, la mesure de distance radar par un immobile de Rindler (tel que si M est un évènement de sa ligne d'univers, alors il existe un évènement O tel que , je change le r en 1/g, toujours constant, et je change le signe car je me place en signature +---).

On a toujours l'évènement A pour le départ du signal, et l'évènement C pour la réception du signal réfléchi. A et C sont sur l'hyperbole, donc .
On va considérer un évènement B si l'objet est plus proche de O que l'immobile et un évènement B' si l'objet est plus loin de O que l'immobile. Dans les deux cas c'est l'évènement de réflexion du signal.
On considère toujours l'évènement D, projeté orthogonal de B (et de B') sur la droite (AC), bien que ce ne soit pas un évènement de la ligne d'univers de l'immobile, il est utile géométriquement (en effet, on peut montrer que OD est orthogonal à AC, ce qui nous permet de connaitre la longueur propre OD par le théorème de pythagore, puis, comme BD est aussi orthogonal à AC est qu'on est en 1+1D, on sait que OB et OD sont colinéaires et on peut donc déduire la longueur propre de OB).
On constate alors que si l'angle entre OA et OD est , alors la distance OB est de et la distance OB' est de . Si on construit l'évènement E sur l'hyperbole, telle que OE soit colinéaire à OD, alors la distance OE est .
La durée écoulée entre A et C pour l'immobile de Rindler est , donc la demi-durée (celle entre A et E ou E et C) est de .



La suite plus tard...

m@ch3

[mach3]

Choisissons un repère de Lorentz tel que O en soit l'origine et que B, B', E et D se produisent au temps coordonné 0, et donnons les coordonnées (t,x) des divers évènements :
O
A
B
B'
C
D
E

puis passons aux coordonnées de Lass (T,X) par transformation suivante :




on a alors :

O(indéfini,-infini)
A
B
B'
C
D
E

Miracle !

La coordonnée spatiale de Lass de B ou B' est la moitié de la durée propre mesuré par l'immobile de Rindler entre A et C!
Ainsi, si l'immobile de Rindler mesure une distance radar de façon naïve, ce n'est pas la distance propre entre un point de sa ligne d'univers et un évènement qui est mesuré, mais la coordonnée spatiale de Lass de l'évènement.

m@ch3

[mach3]

Dans les coordonnées de Lass :
et vu la formule on peut penser que X et T correspondent aux X et T des coordonnées de Rindler.
Dans la formule X et T des coordonnée de Lass on a


comment interpréter x et ?

Attention, dans le tableau de la page wiki, T, X, Y, Z sont des coordonnées de Lorentz, et t, x, y, z sont les coordonnées de Kottler-Moller, de Rindler ou de Lass (ça dépend de la ligne du tableau). Il semble que cela n'ait pas été compris ainsi. La page n'est pas super claire.

En tout cas, on a t(Lass)=t(Rindler) et x(Lass)=ln(g x(rindler)) (ou ln(x(rindler)/Rh) si je reprend votre notation). Lass ramène l'immobile de Rindler en x(Rindler)=1/g en 0, et envoie l'origine x(Rindler)=0 à - l'infini.

m@ch3

[Zefram Cochrane]

Salut m@ch3
merci pour le calcul et les schéma.
Par identification ( http://forums.futura-sciences.com/ph...ml#post6024954) :
on a et

j'ai comme position de départ pour Vert (E sur ton schéma)
Rouge est situé à T=0s à ( B sur ton schéma) et BLeu à (B' sur ton schéma)

, Vert se trouve en en D sur ton schéma lorsque l'onde radar parvient en B et B'
Donc à cet instant, il s'est écoulé depuis le début de l'accélération de Vert une durée propre
et que ceci correspond à la distance radar soit la longueur AD ou BD ou DC ou B'D sur ton schéma.

Notes qu'horsmis le fait que B ne se trouve pas au milieu du segment OE et donc correspond à une vitesse W atteinte par Vert ( l'immobile de Rindler) en C différente de W=(2V)/(1+V²) = 15/17, nos résultats finaux concordent, puisqu'on trouve tous les deux la même expression , même si la manière d'y parvenir diffère.

Maintenant, qu'on a une durée aller-retour pour une onde radar, qu'est ce qui te permets de que la distance radar correspondant à la motié de la durée de détection *c correspond à la distance apparente?

[mach3]

Maintenant, qu'on a une durée aller-retour pour une onde radar, qu'est ce qui te permets de que la distance radar correspondant à la motié de la durée de détection *c correspond à la distance apparente?

La distance radar mesurée par un observateur est la durée propre d'aller-retour d'un signal de genre nul, divisée par 2, par pure convention.
Dans le cas d'un observateur en mouvement rectiligne uniforme en espace-temps plat, il se trouve que ça donne la longueur propre entre un évènement et son projeté orthogonal sur la ligne d'univers de l'observateur, ce qui colle avec l'intuition venue de la physique classique. Si on utilise un système de coordonnée de Lorentz où l'observateur est immobile et passe par l'origine, la distance radar est la coordonnée spatiale de Lorentz, en valeur absolue (en 1+1D, en 1+3D, c'est la norme de partie spatiale du vecteur position).

Dans le cas d'un observateur en mouvement quelconque, la distance radar ne correspond pas, a priori, à quelque chose de concret physiquement. Dans le cas particulier d'un immobile de Rindler, la distance radar est la coordonnée spatiale de Lass, en valeur absolue (en 1+1D, je n'ai pas encore regardé le cas 1+3D).

D'autre systèmes de mesure de distance (via la mesure de taille angulaire, via la mesure de luminosité...) existent et donnent tous le même résultat pour un observateur en mouvement rectiligne uniforme dans l'espace-temps plat. Par contre ils donnent des résultats plus ou moins divergents pour un observateur en mouvement quelconque. La notion de distance perd de sa substance dès qu'on sort du cas de l'observateur inertiel dans l'espace-temps plat, c'est d'ailleurs patent en cosmologie, où on parle de 4 notions différentes de distance, qui ne coïncident à peu près que lorsqu'elles sont faibles. Je n'en ai pas encore eu le temps, mais j'ai pour projet d'étudier ce que donnent ces différentes mesures de distances pour un immobile de Rindler.

m@ch3

[Zefram Cochrane]

Je vais tenter de réfléchir de mon coté au moyen de déterminer la distance radar d'un point quelconque d'un plan spatial X;Y.

Mais j'ai un problème en supposant que la distance radar correspondent à la distance apparente.
: les coordonnée de Lass disent (d'après ton schéma), si je m'éloigne de O en accélérant continuement avec une accélération propre g depuis E et qu'après avoir atteint la vitesse V, je vois B et B' à une distance radar équidistante, alors la distance porpre de B est de ... et celle de B' de .....

ma question est comment calculer la distance radar de B et B' que je n'ai pas encore atteint V et après?
parce qu'en toute état de cause, je verrai bien B et B' à une distance apparente de moi différente de la distance propre, j'en conviens.

[mach3]

Attention, B et B' sont des évènements, pas des objets. L'un et l'autre peut appartenir aux lignes d'univers de deux objets, mais ma démonstration ne fait aucune hypothèse sur le mouvement de ces objets. Elles donnent juste la distance radar de ces objets quand ils passent par ces évènements.
De plus, on suppose que l'observateur est immobile de Rindler au moins de l'évènement A à l'évènement C.

Sinon, c'est quoi exactement une "distance apparente"? Il me parait important que ce soit bien défini...

m@ch3

[Zefram Cochrane]

Bonsoir,
Je vais tenter de reprendre les paramètres de ton schéma.
Soit K le référentiel de O, B et B' que nous allons appeler le paysage. Soit K' le référentiel de O', un observateur en TRU à par rapport à K.
Pour éviter tout malentendu, j'appelle référentiel un volume d'espace dans lequel je puis tendre une règle entre deux point stationnaires dans ce référentiel.
Donc, la distance apparente entre O' et B correspond à la longueur d'une règle étendue dans le référentiel K' entre O' et la position observée de B lorsque O' se trouve à la coordonnée spatiale à .
Ma question est : Est-ce que cette distance apparente correspond à la distance apparente observée par O° l'observateur immobile de Rindler, comobile avec O' à T?
Bien entendu cette distance apparente ne correspondra pas à la longueur propre de séparant O° de B à T=0s : .

Cordialement, Zefram

(Je pense que oui car mesurer une distance apparente est une mesure locale de distance donc entrant dans le cadre édicté par le principe de Wolfgang Rindler.)

[mach3]

Bonsoir,
Je vais tenter de reprendre les paramètres de ton schéma.
Soit K le référentiel de O, B et B' que nous allons appeler le paysage. Soit K' le référentiel de O', un observateur en TRU à par rapport à K.
Pour éviter tout malentendu, j'appelle référentiel un volume d'espace dans lequel je puis tendre une règle entre deux point stationnaires dans ce référentiel.
Donc, la distance apparente entre O' et B correspond à la longueur d'une règle étendue dans le référentiel K' entre O' et la position observée de B lorsque O' se trouve à la coordonnée spatiale à .
Ma question est : Est-ce que cette distance apparente correspond à la distance apparente observée par O° l'observateur immobile de Rindler, comobile avec O' à T?
Bien entendu cette distance apparente ne correspondra pas à la longueur propre de séparant O° de B à T=0s : .

Cordialement, Zefram

(Je pense que oui car mesurer une distance apparente est une mesure locale de distance donc entrant dans le cadre édicté par le principe de Wolfgang Rindler.)

O, B et B' sont des évènements, pas des objets ou des observateurs. Ca ne sert à rien de dire qu'on reprend les paramètres pour les modifier une ligne plus bas...
La notion de référentiel utilisé semble être celle de référentiel rigide.
La mesure de distance à la règle pose des problèmes : comment étalonne-t-on la règle? quelles sont les propriétés mécaniques de la règle (élasticité, plasticité...) qui risquent d'impacter sa longueur propre (et sa rectitude!), de façon réversible ou non en fonction des contraintes qu'elle peut subir suite à des mouvements accélérés, sachant qu'une rigidité "infinie" est exclue? Je n'aime pas les mesures à la règle dans le cadre relativiste, il faut faire trop d'hypothèse sur la règle, ou alors il faut passer son temps à la ré-étalonner par un autre moyen de mesure (distance radar, par exemple), autant alors utiliser directement cet autre moyen de mesure... Ou, à la rigueur, supposer qu'il y a des règles étalonnées partout et qui flottent en divers mouvements rectilignes uniformes et que les observateurs peuvent utiliser celles qui conviennent au moments opportuns sans y toucher, mais alors on s'éloigne du concret et on est complétement dans l'expérience de pensée détachée de la réalité physique.

Pour répondre correctement à la question, il va falloir que l'énoncé soit posé de façon encore plus précise, en listant bien les différentes lignes d'univers, leurs caractéristiques, et les évènements clés, en précisant bien le système de coordonnées utilisé le cas échéant. Pour l'instant j'ai peur de ne pas interpréter l'énoncé de la bonne manière.
Pour ce que je comprend pour l'instant, il est question de distances que mesure un observateur en mouvement rectiligne uniforme dont la ligne d'univers fait un angle avec le segment AC, et plus précisément de distance mesuré alors que cet observateur est en l'évènement C. Toujours de ce que je comprend, il essaie de mesurer la distance d'un objet ayant mouvement parallèle à AC et passant par l'évènement B.
Est-ce bien de cela dont il est question?

m@ch3

[Zefram Cochrane]

Bonjour,


Sur ce schéma : on a Orang situé à 30s.l derrière Vert à T=0s. Vert accélère de manière à ce que et lorsqu'il atteint Rouge situé à 37.5s.l de Orange à T=22.5s , Vert est comobile avec Bleu ( pour te montrer que j'ai compri ce concept : la position de Vert coïncide avec celle de Bleu et ils ont la même vitesse relative par rapport à Orange et Rouge).
Bleu trâine derrière lui une règle rigide de 10s.l de longeur propre. Comme il est en MRU à V=0.6c, à tout instant Bleu voit que sur les 10s.l de la longueur apparente de sa règle, se répartissent 20s.l de longueur de voie représentée en jaune.
Si la règle était oroentée vers l'avant, le rapport serai inversé. Pourtant, du point de vue de Bleu, la longueur apparente de sa règle est la même qu'elle soit orienté dans n'importe quelle direction.

Ma question est si j'avais représenté un cercle de 10s.l de rayon autour de Bleu, est ce qu'à l'instant précis où Vert est comobile avec Bleu, il verrait autour de lui un cercle de 10s.l de rayon autour de lui?

[mach3]

L'image n'est pas encore validée, mais vu le texte, je doute que cela réponde à ma question...

m@ch3

[mach3]

Voila, c'est validé, un dessin où on ne comprend quasiment rien, comme d'habitude...

Pas évident d'avoir une discussion quand l'interlocuteur ne fait pas d'effort pour être compris.

m@ch3

[Zefram Cochrane]

Bon,
je vais essayer d'être plus clair.
Soit Vert un observateur au milieu d'un wagon (rectangle vert) en MRU à V=0.8c par rapport à la voie.

A T=0s, Vert traverse le milieu d'un champ circulaire (en orange) avec des bornes (points orange)
mais comme sa vitesse relative vis-à-vis du champ est de V=0.8c, il ne verra pas à T=0s le champ circulaire mais il le verra elliptique (en vert) et la distance apparente le séparant des bornes (points vert) est parfaitement calculable.
A T=0s, Vert verra la borne 1 à telle distance, A T=0s Vert verra la borne 2 à telle distance, etc...

Ma question est si Violet en accélération constante à une position qui coincide avec Vert à T=0s et avec une vitesse égale à V aura la même perception du champ que Vert?

autre manière d'aborder le problème: si à T=0s, Vert accélère brutalement depuis la plateforme du wagon, est ce que sa perception du champ à T=0s variera ?

J'espère avoir été clair dans ma question .
Mes excuses par avance si ce n'est toujours pas le cas.

[Mailou75]

Salut,

Ma question est si Violet en accélération constante à une position qui coincide avec Vert à T=0s et avec une vitesse égale à V aura la même perception du champ que Vert?

(Pas déjà répondu ?)

Oui, car le fait d'être en accélération amène ton observateur en un évènement précis avec une vitesse instantanée donnée et c'est tout ce qui compte. Si un autre observateur en MRU passe par cet évènement avec la même vitesse, les deux verront la même chose. (Vitesse = trajectoire 4D à moins d'avoir un référentiel "fixe" pour parler de vitesse, ton champ rond par exemple)

......

Miracle !
La coordonnée spatiale de Lass de B ou B' est la moitié de la durée propre mesuré par l'immobile de Rindler entre A et C!

Jolis dessin et démonstration, bravo !

Dans le cas d'un observateur en mouvement quelconque, la distance radar ne correspond pas, a priori, à quelque chose de concret physiquement.

Bah si, à la distance propre entre deux évènements B et B' dans l'espace euclidien du voyageur à mi-temps (cad pas à mi parcours a priori, sauf dans le cas précis de ta figure où le voyageur fait un aller retour depuis le même point dans l'espace qui nous intéresse) et entre lesquels il doit pouvoir, par reconstruction s'il connaît son accélération, estimer sa position, à mi-temps... Par contre on peut sérieusement se demander à quoi ça sert, surtout si cet espace n'a rien de concret ?

Voila, c'est validé, un dessin où on ne comprend quasiment rien, comme d'habitude...
Pas évident d'avoir une discussion quand l'interlocuteur ne fait pas d'effort pour être compris.

C'est agaçant hein... maintenant y'a les dessins, ça reste des hiéroglyphes mais si on cherche y'a du bon au fond

(...)je doute que cela réponde à ma question...

Stéphanie de Monaco ! Vous pouvez répéter la question ? (svp)

[mach3]

Pour la question, voir à la fin du message 19.

@Zef : pas encore eu le temps de travailler sur le problème, pas sur d'avoir le temps ce week-end. Mais c'est intéressant car ça va dans le sens des choses que je voulais explorer prochainement.

m@ch3

[Zefram Cochrane]

Bonjour,

(Pas déjà répondu ?)
Oui, car le fait d'être en accélération amène ton observateur en un évènement précis avec une vitesse instantanée donnée et c'est tout ce qui compte. Si un autre observateur en MRU passe par cet évènement avec la même vitesse, les deux verront la même chose. (Vitesse = trajectoire 4D à moins d'avoir un référentiel "fixe" pour parler de vitesse, ton champ rond par exemple)

Je suis d'accord mais j'ai ouvert ce fil pour vérifier ce point plus spécifiquement.

Bah si, à la distance propre entre deux évènements B et B' dans l'espace euclidien du voyageur à mi-temps (cad pas à mi parcours a priori, sauf dans le cas précis de ta figure où le voyageur fait un aller retour depuis le même point dans l'espace qui nous intéresse) et entre lesquels il doit pouvoir, par reconstruction s'il connaît son accélération, estimer sa position, à mi-temps... Par contre on peut sérieusement se demander à quoi ça sert, surtout si cet espace n'a rien de concret ?

La distance propre entre Rouge et Vert et la distance propre entre Vert et Bleu correspond à la distance spérant Rouge de Vert et Bleu de Vert à T=0s pour V=0.6c
J'ai répertorié les différents points du schéma de mach3


lorsque Vert atteint 0.6c à T=20.79s il verra Rouge et Bleu simultanément tels qu'ils étaient à T=0s. la distance séparant le point de coordonnées des point et est

Maintenant je ne pense pas que l'on puisse affirmer que cette distance radar correspondent à la distance apparente parce qu'il faudrait alors expliquer pourquoi la simultanée serait relative si Vert était en MRU à V=0.6c et ne le serait plus parce qu'il est en MRUA à g.
(mais bon. sait-on jamais!)

[Archi3]

Attention, B et B' sont des évènements, pas des objets. L'un et l'autre peut appartenir aux lignes d'univers de deux objets, mais ma démonstration ne fait aucune hypothèse sur le mouvement de ces objets. Elles donnent juste la distance radar de ces objets quand ils passent par ces évènements.
De plus, on suppose que l'observateur est immobile de Rindler au moins de l'évènement A à l'évènement C.

de ce que j'ai compris de la notion de distance en RG , c'est :
* il n'y en général pas de "distance" définie univoquement entre deux évènements quelconques

* il n'y a pas non plus de "distance" définie univoquement entre deux objets immobiles dans le référentiel, sauf dans certains référentiels (voir plus bas)

* il y a une distance infinitésimale définie univoquement entre deux objets immobiles infiniment proches, mais qui peut dépendre du temps : c'est la distance radar, qui a donc bien un interprétation physique pour des objets proches : c'est leur distance réelle physique, mesurée par des règles.

* en général, l'intégration de cette distance infinitésimale dépend du chemin suivi dans l'espace temps donc il n'y a pas de distance univoque entre deux objets lointains, mais dans certains cas, cette distance peut exister et etre bien définie, en particulier quand la métrique est diagonale et indépendante du temps, ce qui est le cas de la métrique de Rindler : donc la différence de coordonnées Lass = radar est bien la distance propre entre deux observateurs immobiles dans le référentiel de Rindler, qui est indépendante du temps : la métrique de Rindler est donc bien "rigide" au sens où la distance propre entre deux observateurs immobiles dans Rindler ne varie pas. En revanche elle ne couvre pas tout l'espace-temps, il n'y a que les coordonnées de Lorentz initiales qui sont rigides et couvrent tout l'espace temps (ce qui définit un référentiel inertiel).

[Archi3]

* il y a une distance infinitésimale définie univoquement entre deux objets immobiles infiniment proches, mais qui peut dépendre du temps : c'est la distance radar, qui a donc bien un interprétation physique pour des objets proches : c'est leur distance réelle physique, mesurée par des règles.

PS : j'entends par immobiles le fait qu'ils sont à coordonnées constantes dans le référentiel, ce qui ne signifie pas que leur distance est constante, donc ils peuvent etre tous immobiles et avoir néanmoins une vitesse relative, c'est le cas de l'expansion de l'Univers !

[invite6c093f92]

Je me demande si le pdf mis plus haut a été lu...

[Archi3]

le pdf que tu as posté dit bien que le référentiel de Rindler et "rigide" au sens ci-dessus ( la distance propre entre deux observateurs "rindler immobiles", à coordonnées de Rindler constante, reste constante), mais que c'est une propriété particulière au référentiel de Rindler (et aux référentiels inertiels).

“Rigidité du référentiel de Rindler...
En ce sens précis la ligne de coordonnée x = const. peut être considérée comme un “axe rigide” et on peut concevoir la matérialisation du repère de Rindler par un solide accéléré le long de l’axe X du repère inertiel S. Cette propriété est particulière au repère de Rindler; dans le cas général il faut abandonner la notion de repère “rigide” et de référentiel “solide” sauf s’ils sont inertiels.