Principe de wolfgang rindler

[invite6c093f92]

...

Oui, aucun soucis avec tes posts, sinon je t'aurais quoté mais c'est vrai que à la suite, comme ça, ça pouvait porter à confusion.
C'était une remarque générale.
-----

[Mailou75]

Salut,

Je suis d'accord mais j'ai ouvert ce fil pour vérifier ce point plus spécifiquement.

Ok je te laisse verifier.

J'ai répertorié les différents points du schéma de mach3

Joli, ton schéma prouve que la distance Radar pour les accélérés de Rindler est celle de la longueur propre qui les sépare (constante). Il serait encore plus efficace si tu nottais le temps propre de l'accéléré pour monter que la ligne verte croise sa trajectoire a "mi temps"

[mach3]

Joli, ton schéma prouve que la distance Radar pour les accélérés de Rindler est celle de la longueur propre qui les sépare (constante). Il serait encore plus efficace si tu nottais le temps propre de l'accéléré pour monter que la ligne verte croise sa trajectoire a "mi temps"

euh... Non... La distance radar entre immobiles de Rindler n'est pas la longueur propre qui les sépare. Preuve : l'événement O est à 1/g de l'immobile en Xrindler=1/g alors que distance radar que mesure cet immobile pour O est infinie

m@ch3

[Zefram Cochrane]

Bonsoir,
Je pense que l'on peut faire de nombreux rapprochement entre l'horizon de Rindler et celui de Schwarzschild.
La longueur propre entre un accéléré de Rindler et l'horizon de Rindler est la Rh=c²/g. il correspond dans la métrique de Schwarzschild à la longueur d'une corde tendue radialement entre un accéléré stationnaire dans un champ de gravitation et l'horizon d'un TN http://forums.futura-sciences.com/as...ml#post4618580.

De même, si un accéléré stationnaire à la coordonnée r du centre d'un TN, envoie une onde radar sur l'horizon d'un TN, il n'en reverra jamais l'écho, sa "distance radar" sera oo.
pourtant, on ne peut pas affirmer que la distance apparente séparant l'observateur du TN sera oo pour autant.

Je trouve que ce schéma de Mailou pour le diagramme KS: http://forums.futura-sciences.com/as...ml#post5810148
est très ressemblant avec celui de mach3 sur ce fil.

http://forums.futura-sciences.com/as...ml#post5826580
celui ci également.
Je me demande si on peut s'en servir pour établir une distance radar à la Rindler comme je l'ai fait sur mon schéma précédent avec KS?

[Mailou75]

Salut,

euh... Non... La distance radar entre immobiles de Rindler n'est pas la longueur propre qui les sépare. Preuve : l'événement O est à 1/g de l'immobile en Xrindler=1/g alors que distance radar que mesure cet immobile pour O est infinie

Ah oui on est sur un cas particulier, j'me suis fait avoir

Je me demande si on peut s'en servir pour établir une distance radar à la Rindler comme je l'ai fait sur mon schéma précédent avec KS?

Des lors qu'on definit la "distance radar" comme "la moitié du temps propre d'aller-retour du signal" pourquoi pas...

[Archi3]

euh... Non... La distance radar entre immobiles de Rindler n'est pas la longueur propre qui les sépare. Preuve : l'événement O est à 1/g de l'immobile en Xrindler=1/g alors que distance radar que mesure cet immobile pour O est infinie

m@ch3

la notion de distance d'un évènement n'a pas de sens : il n'y a (éventuellement) que des distances entre observateurs, qui doit etre évaluée "au même temps" ce qui n'existe que lorsque le référentiel est synchronisable. Ce n'est pas le cas pour le point O qui n'a pas d'observateur immobile associé. Pour les observateurs immobiles à x> 0 , la distance radar est bien la longueur propre qui les sépare.

[mach3]

la notion de distance d'un évènement n'a pas de sens

Ben, si, ça a du sens. Quand on mesure une distance radar à un objet en mouvement quelconque, on fait la mesure sur un évènement de la ligne d'univers de l'objet. Avant d'être la distance radar à l'objet, c'est la distance radar à l'évènement, dans le même sens d'ailleurs (quand on est inertiel et dans l'espace-temps plat) que la distance d'un point à une droite en géométrie euclidienne. En tout cas c'est ainsi que moi je l'entends dans tous mes posts, et c'est pratique parce que ça permet de ne faire aucune hypothèse ou précision sur le mouvement de l'objet : on ne mesure qu'un évènement de la ligne d'univers de l'objet, qu'importe la ligne d'univers. C'est aussi pratique parce qu'on n'a même pas besoin de la notion de référentiel ou de système de coordonnée, c'est une relation purement géométrique, très primitive. Le concept de distance d'usage courant est différent et relativement élaboré, avec plein de sous-entendu et de conventions (référentiel, synchronisation, etc...).

Pour les observateurs immobiles à x> 0 , la distance radar est bien la longueur propre qui les sépare.

Faux.

m@ch3

[mach3]

Faux.

et pour être précis, si un immobile de Rindler mesure une distance radar de , la longueur propre est de ou .

m@ch3

[mach3]

Bonsoir,
Je pense que l'on peut faire de nombreux rapprochement entre l'horizon de Rindler et celui de Schwarzschild.

oui, mais attention aux rapprochements hatifs. Ce sont quand deux choses intrinsèquement différentes

La longueur propre entre un accéléré de Rindler et l'horizon de Rindler est la Rh=c²/g. il correspond dans la métrique de Schwarzschild à la longueur d'une corde tendue radialement entre un accéléré stationnaire dans un champ de gravitation et l'horizon d'un TN http://forums.futura-sciences.com/as...ml#post4618580.

De même, si un accéléré stationnaire à la coordonnée r du centre d'un TN, envoie une onde radar sur l'horizon d'un TN, il n'en reverra jamais l'écho, sa "distance radar" sera oo.
pourtant, on ne peut pas affirmer que la distance apparente séparant l'observateur du TN sera oo pour autant.

c'est quoi une distance apparente (dans le contexte de la relativité générale, voir le post de Archi3 d'hier matin)?

Je me demande si on peut s'en servir pour établir une distance radar à la Rindler comme je l'ai fait sur mon schéma précédent avec KS?

Il suffit de trouver le changement de coordonnées qui va bien, vers des coordonnées qui sont conformes et dans lequel les immobiles de Schwarzschild occupent des coordonnées spatiales constantes. Ce ne sont pas les coordonnées de Kruskal (elles sont conformes mais les immobiles de Schwarzschild n'y sont pas immobiles). Il faut transformer r et t en de nouvelles coordonnées r' et t' telles que :
-t' coïncide avec le temps propre d'un immobile de Schwarzschild particulier (c'est ce qu'on fait avec la coordonnée temporelle de Rindler, elle coïncide avec le temps propre d'un immobile de Rindler en particulier)
-les coefficients devant dr'² et dt'² dans l'écriture de la métrique sont égaux au signe près (et à c près selon le choix pour les unités)
Ainsi, pour l'immobile de Schwarzschild sélectionné, qui sera vraisemblablement en r'=0 si on a eu l'esprit pratique en faisant le changement de coordonnées, la distance radar qu'il mesurera entre lui et un autre immobile de Schwarzschild, situé sur la même radiale, sera égale en valeur absolue à la coordonnée r', et ce sera la moitié de la durée de l'aller-retour mesurée par l'immobile sélectionné. L'horizon futur sera localisé vers -l'infini en r' et vers +l'infini en t' dans ces nouvelles coordonnées (note : en Schwarzschild, il est en r=Rs et t=+l'infini, pour rappel il n'y a aucun évènement en r=Rs et t=valeur finie, ces points là n'existe que sur la carte, pas sur le territoire).

m@ch3

[Zefram Cochrane]

Bonjour,
R : coordonnée r.
Rb: coordonnée r de Bleu
Rr : coordonnée r de Rouge


la distance percourue par la lumière entre Rouge et Bleu, C'est ce qui permet de retrouver l'effet Shapiro pour une trajectoire radiale et c'est ce qui correspond chez Rindler à la distance radar entre Rouge et Bleu, pour Bleu; pour la distance radar entre Bleu et Rouge pour Rouge, il faut inverser Rr et Rb dans les équiations.

la longueur d'une corde tendue entre Rouge et Bleu. Elle correspond à la longueur propre chez Rindler.


Si j'en suis la métrique de Schwarzschild, pour dt'=dt=0s:
La distance apparente entre Rouge et Bleu serait pour Rouge

et pour Bleu :


as tu eu le temps de te pencher sur ce message ?
http://forums.futura-sciences.com/ph...ml#post6027475

[Mailou75]

Salut,

Faux.

Je confirme, si c'était le cas ça s'apellerait les coordonnées de Rindler

Là je bute sur Kottler-Moller, je ne sais pas du tout ce que je dois obtenir. Autant pour Lass on sait où on va et chaque réferentiel pour un accéléré particulier est identique à un autre accéléré, aux unités/echelle près, autant pour KM le choix de l'accéléré modifie la figure. Qqun saurait il me dire quelle est la particularité de ce système, que "verifie"-t il pour savoir si je ne dessine pas n'importe quoi ? (Pour l'instant je trouve qu'il ne verifie rien de spécial, tout est en courbes lambda, et me pose donc des questions sur son utilité). Je ne comprends pas non plus la colone de gauche dans le lien wiki car pour moi, avec les formules donnees, à T=0, Minko donne X=1/a, Rindler x=1/a, Lass x'=0 (pour a donné) et KM x"=1/a. Ca ne colle donc pas avec le tableau et me met encore plus le doute...

Merci

Mailou

[Mailou75]

la distance percourue par la lumière entre Rouge et Bleu, C'est ce qui permet de retrouver l'effet Shapiro pour une trajectoire radiale et c'est ce qui correspond chez Rindler à la distance radar (...)

Interessant, je me posais la question dans les tout premiers posts du fil que tu cites sur KS, j'avais bien l'impression que c'était le cas mais sans certitude. T'es sur de ton coup ?
(J'ai l'impression que quand on aura defini comment un accéléré de Rindler voit ses congénaires evoluer au cours du temps on ne sera plus trés loin de pouvoir definir comment un stationnaire voit les autes chez KS)

[Zefram Cochrane]

Salut,

Je confirme, si c'était le cas ça s'apellerait les coordonnées de Rindler


Mailou

faux voici un schéma (sommaire) pour comprendre indexé par les durée propres réciproques.


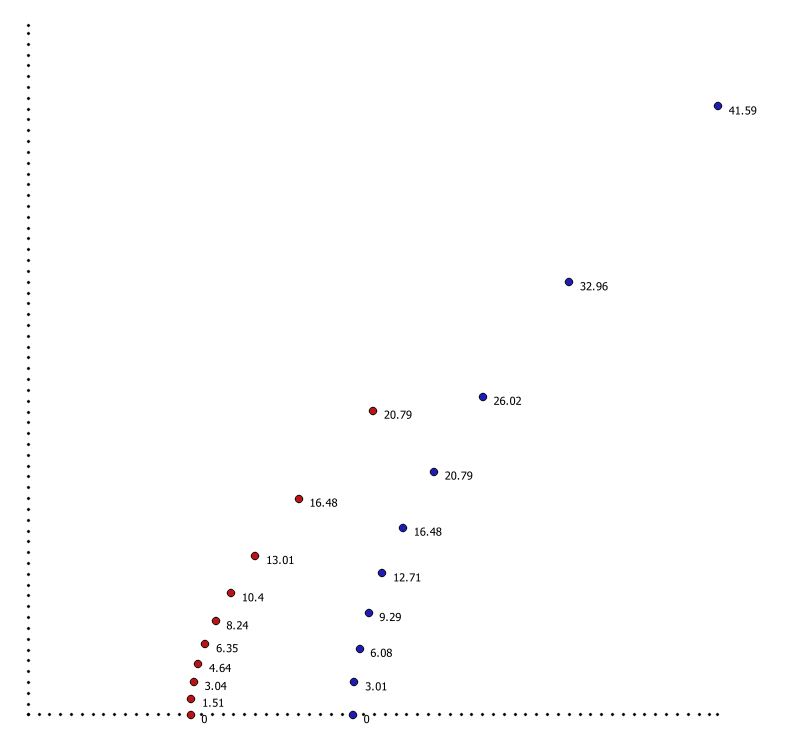
la longueur propre est la distance séparant Rouge et Bleu à T=Tr°=Tb°=0s.
si je considère les capsules de Rouge et Bleu comme ponctuelles ( longueur unitaire = diamètre d'une capsule), je peux créer une chaîne de n capsules entre Rouge et Bleu à T=0s. Et si chaque capsule dispose d'un système de propulsion, à T=0s chaque capsule peut accélérer de manière à ce que la chaîne ne se brise pas (paradoxe de la ficelle de Bell).
A tout instant n'importe quel observateur situé dans une capsule de cette chaîne, la verra constituée de n capsules.
La longueur propre n'est pas égale à la distance-radar.

@+ Zefram

[mach3]

as tu eu le temps de te pencher sur ce message ?
http://forums.futura-sciences.com/ph...ml#post6027475

Hélas, pas encore, et il va falloir être patient, je ne vais pas disposer de moments assez long pour me poser sur le sujet dans les jours qui viennent.

Là je bute sur Kottler-Moller, je ne sais pas du tout ce que je dois obtenir.

Si je pars de Lorentz, (t,x), j'accède a Rindler en faisant (ath(t/x)/g , )
Au lieu de ça, je fais d'abord une translation de 1/g vers les x croissants, mon Lorentz devient (t, x+1/g). Je fait la même transformation que pour accéder a Rindler en partant de (t,x), j'obtiens (ath(t/(x+1/g))/g , ). Je retranslate de 1/g dans l'autre sens et paf, Kottler-Moller.

Il semblerait dès lors qu'au lieu de s'intéresser à un immobile de Rindler d'accélération propre g et de vitesse nulle en (0,1/g) on s'intéresse à un immobile de Rindler d'accélération propre g et de vitesse nulle en (0,0). En effet, la première translation de 1/g vers les x croissants transporte cet immobile de (0,0) à (0,1/g), ce qui nous ramène à une situation "connue" (celle de immobile de Rindler d'accélération propre g et de vitesse nulle en (0,1/g) ). On transforme alors en Rindler, puis, on ramène l'immobile, alors en coordonnée spatiale 1/g en coordonnée spatiale 0 en translatant de 1/g vers les x négatifs.

Donc Kottler-Moller, c'est du Rindler translaté de 1/g vers les x négatifs.

C'est assez logique de vouloir décrire le point de vue d'un accéléré en le plaçant à l'origine du repère, c'est pourquoi les coordonnées de Kottler-Moller sont plus anciennes. Par contre les coordonnées de Rindler sont plus "symétriques", en plaçant l'intersection entre les horizons passé et futur x=0.

m@ch3

[Zefram Cochrane]

Interessant, je me posais la question dans les tout premiers posts du fil que tu cites sur KS, j'avais bien l'impression que c'était le cas mais sans certitude. T'es sur de ton coup ?

pour Shapiro et Lass, très certain:

https://fr.wikipedia.org/wiki/Effet_Shapiro
L'effet Shapiro peut être mesuré dans le Système solaire, notamment par l'étude des temps d'arrivée des signaux émis par un atterrisseur posé sur une autre planète. La première réalisation précise de la mesure de l'effet Shapiro a ainsi été faite par les sondes Viking posées sur Mars4. Auparavant, l'effet Shapiro avait été mis en évidence par l'étude de l'écho radar émis depuis la Terre et réfléchi sur une autre planète. Cette première méthode était relativement imprécise du fait que l'écho reçu était extrêmement faible (10−21 W pour un signal émis de 300 kW) et du fait que la surface de la planète sur laquelle se réfléchissait le signal était relativement grande. À l'inverse, les signaux émis depuis un atterrisseur sur une planète étaient nettement plus précis, mais d'un coût considérablement plus élevé car nécessitant l'envoi d'une sonde spatiale vers une planète.

(J'ai l'impression que quand on aura defini comment un accéléré de Rindler voit ses congénaires evoluer au cours du temps on ne sera plus trés loin de pouvoir definir comment un stationnaire voit les autes chez KS)

moi aussi. J'attends de voir si màch3 est d'accord avec ma définition de la distance apparente parce que je sais comment un accéléré voit ses petits copains évoluer. Après il sera intéressant de voir ce que cela donnera chez KS et si c'est raccord avec Schwarschild dont j'ai donné la formule un peu plus haut.

[Zefram Cochrane]

Hélas, pas encore, et il va falloir être patient, je ne vais pas disposer de moments assez long pour me poser sur le sujet dans les jours qui viennent.

Pas de problème prends ton emps

[Mailou75]

Je suis d'accord mais j'ai ouvert ce fil pour vérifier ce point plus spécifiquement.

Finalement la question n'est pas inintéressante. Une source vue radialement semble t elle plus loin si la lumiere affiche un temps de parcours different depuis d'une souce sans masse ? On a a priori envie de dire oui, la lumiere d'une etoile a proximité du soleil est vue ailleurs et plus loin, et puis sinon quelle difference y aurait il ? Puis on se dit qu'appliqué au trou noir, on verrait toujours celui ci a l'infini (Radar). Donc on a plus de raison de penser qu'on voit une projection du cone passé sur le plan euclidien (perpendiculaire a la trajectoire localement), plutot que "la meme chose" en tenant compte ce qui est vu tient au temps de parcours du photon dans un referentiel donné (surtout quand l'observateur en change). Pourtant en cosmo l'univers visble mesure 13,7GaL de rayon... (HS) et si tu remet ça en cause alors tu remets en cause les bases de l'aberration ! Mais c'est bien de mettre les pieds dans le plat... Une piste peut etre, dans le dernier schema que j'ai link (Horizon de Zef 3D ) on voit que le voyageur et l'inertiel Bleu voient les objets a des endroits differents est a des longeurs radar diferentes, a priori. Pourtant il s'agit du meme photon lu differemment.. ?

[Archi3]

Ben, si, ça a du sens. Quand on mesure une distance radar à un objet en mouvement quelconque, on fait la mesure sur un évènement de la ligne d'univers de l'objet. Avant d'être la distance radar à l'objet, c'est la distance radar à l'évènement, dans le même sens d'ailleurs (quand on est inertiel et dans l'espace-temps plat) que la distance d'un point à une droite en géométrie euclidienne.

oui ok, tu peux définir la distance d'un évènement à un observateur A comme la distance d'un autre observateur B qui serait immobile dans le référentiel et coïnciderait avec l'évènement, ça revient au meme. Mais ça n'est possible que si tu sais dire quel évènement de A est simultané avec B, et ça ce n'est pas possible de manière générale dans tout l'espace. Sauf cas particuliers, et justement les référentiels inertiels et celui de Rindler appartiennent à ces cas là (du coup c'est possible pour ceux là).

En tout cas c'est ainsi que moi je l'entends dans tous mes posts, et c'est pratique parce que ça permet de ne faire aucune hypothèse ou précision sur le mouvement de l'objet : on ne mesure qu'un évènement de la ligne d'univers de l'objet, qu'importe la ligne d'univers. C'est aussi pratique parce qu'on n'a même pas besoin de la notion de référentiel ou de système de coordonnée, c'est une relation purement géométrique, très primitive. Le concept de distance d'usage courant est différent et relativement élaboré, avec plein de sous-entendu et de conventions (référentiel, synchronisation, etc...).

tu ne peux pas te passer de la notion de référentiel pour la notion de distance, c'est déjà vrai meme pour les référentiels inertiels à cause de la contraction de Lorentz ! (justement parce que le temps de A "simultané" avec B n'est pas le meme dans les différents référentiels) : il n'y a pas de notion de distance plus simple que celle "d'usage courant".

Faux.

m@ch3

ce n'est pas la différence de coordonnée radar, mais c'est la distance radar au sens où tu l'as défini (le temps d'un aller-retour d'un signal lumineux multiplié par c/2)

[mach3]

Bon, Archi3, je pense qu'on ne se mettra pas d'accord car on n'utilise pas les mêmes définitions.

Pour moi il y a une notion de distance plus simple que celle d'usage courant, c'est la distance radar naïve (j'ajoute naïve comme ça on évitera d'éventuelles confusions) : un observateur, peu importe son mouvement, mesure la durée (dans son temps propre) d'aller-retour d'un signal de genre nul, divise par 2 pour obtenir la distance radar naive et décrète que c'est la distance radar naive qu'il y a entre lui et l'évènement mesuré, pour une date se situant pile entre le départ et l'arrivée du signal. C'est absolu, invariant (tel observateur, a tel évènement de sa ligne d'univers, mesurera telle distance radar naive à tel autre évènement, quelque soit le référentiel ou le système de coordonnées), utilisable dans toutes conditions, et ça a le bon gout de donner la même chose que d'autre mesures de distances si le mouvement de l'observateur est rectiligne uniforme dans un espace-temps plat (situation où le concept de distance d'usage courant, avec tout le bordel de la synchronisation et des référentiels, est clair et sans ambiguïté).

m@ch3

[Mailou75]

Salut,

Donc Kottler-Moller, c'est du Rindler translaté de 1/g vers les x négatifs.

C'est assez logique de vouloir décrire le point de vue d'un accéléré en le plaçant à l'origine du repère, c'est pourquoi les coordonnées de Kottler-Moller sont plus anciennes. Par contre les coordonnées de Rindler sont plus "symétriques", en plaçant l'intersection entre les horizons passé et futur x=0.

D'accord pour l'explication malheureusement ce n'est pas ce que j'obtiens, en KM l'accéléré dont c'est le referentiel n'est pas en (0;0).

Prenons une application numerique : Je tente de faire le repere de l'accéléré à 0,05c/s
L'origine de sa trajectoire hyperbolique en Minko de se trouve à (20sl;0) en coordonées de KM ce même point se trouve aussi à (20sl;0) qui n'est donc pas l'origine. Ensuite je prend un point aléatoire de Minko a représenter dans le repère de cet accéléré. Par exemple (15sl;15s), au pif... et bien se point se trouvera en coordonnées de KM à (11,62..;9,16..) est ce juste ? NB si je change d'accéléré en prenant a=0,01c/s ce point se trouvera alors en (10;6,93..). Il n'y aurait apparement aucune proportionnalité entre les KM pour des accélérés differents.

Merci, pour eviter de diffuser n'importe quoi...

[Mailou75]

faux voici un schéma (sommaire) pour comprendre indexé par les durée propres réciproques.
(...)
La longueur propre n'est pas égale à la distance-radar.

Pourquoi "faux"? On est d'accord. J'ai lu ta premiere figure en diagonale et fait des conclusions aussi hatives que fausses, mais je me suis repenti depuis (y'a plus qu'a convaincre Archi3)

[Zefram Cochrane]

Bonsoir,
Sur le dernier schéma que j'ai fait, la distance propre entre Rouge et Bleu est de 15 s.l; la distance radar entre Rouge et Bleu est de 10.4s.l pour Rouge et de 16.48s.l pour Bleu.

[mach3]

Salut,


D'accord pour l'explication malheureusement ce n'est pas ce que j'obtiens, en KM l'accéléré dont c'est le referentiel n'est pas en (0;0).

Prenons une application numerique : Je tente de faire le repere de l'accéléré à 0,05c/s
L'origine de sa trajectoire hyperbolique en Minko de se trouve à (20sl;0) en coordonées de KM ce même point se trouve aussi à (20sl;0) qui n'est donc pas l'origine. Ensuite je prend un point aléatoire de Minko a représenter dans le repère de cet accéléré. Par exemple (15sl;15s), au pif... et bien se point se trouvera en coordonnées de KM à (11,62..;9,16..) est ce juste ? NB si je change d'accéléré en prenant a=0,01c/s ce point se trouvera alors en (10;6,93..). Il n'y aurait apparement aucune proportionnalité entre les KM pour des accélérés differents.

Merci, pour eviter de diffuser n'importe quoi...

ben, c'est pourtant ça, je viens de revérifier.

Considérons un premier repère de Lorentz (t,x) dans lequel un objet uniformément accéléré, avec une accélération propre de g, passe par l'évènement (0,0) avec une vitesse nulle. Son équation paramétrée est (on peut vérifier qu'en dérivant une première fois par rapport à tau, on obtient un vecteur de norme 1 = 4-vitesse et qu'en dérivant une seconde fois, on obtient un vecteur de norme g = 4-acceleration, orthogonal à la 4-vitesse). Si je transforme les coordonnées pour obtenir celles de Rindler (de paramètre g), on a :




L'équation paramétrée devient donc , , une ligne verticale dans le repère de Rindler, passant par (0,1/g)

Considérons un second repère de Lorentz (t'=t , x'=x-1/g). Dans ce repère, l'objet précédent à pour équation paramétrée . Si je transforme pour obtenir les coordonnées de Kottler Moller à partir de ce second repère de Lorentz, on a :




L'équation paramétrée devient donc , une ligne verticale dans le repère, passant par (0,0)

CQFD

m@ch3

[Mailou75]

Salut,

ben, c'est pourtant ça, je viens de revérifier.

C'est gentil de t'occuper de mon cas, merci

L'équation paramétrée devient donc , une ligne verticale dans le repère, passant par (0,0)

CQFD

Joli ! En tout cas ça donnerait du sens à ce repere, j'ai bien fait de poser la question je partais dans le decors...
Je vais essayer de trouver la coquille et au moins je sais vers où je dois aller maintenant.

Merci

[Mailou75]

Alors voilà... pour obtenir ce que tu dis pour la trajectoire de l'accéléré dans son repère de KM je dois prendre (avec x et t coordonnées en Minko) :

et non pas

et non pas

Et ça ne garantit rien sur tout le reste ! Comprend pô...

Merci

[Archi3]

Bon, Archi3, je pense qu'on ne se mettra pas d'accord car on n'utilise pas les mêmes définitions.

Pour moi il y a une notion de distance plus simple que celle d'usage courant, c'est la distance radar naïve (j'ajoute naïve comme ça on évitera d'éventuelles confusions) : un observateur, peu importe son mouvement, mesure la durée (dans son temps propre) d'aller-retour d'un signal de genre nul, divise par 2 pour obtenir la distance radar naive et décrète que c'est la distance radar naive qu'il y a entre lui et l'évènement mesuré, pour une date se situant pile entre le départ et l'arrivée du signal.

ça a du sens pour les objets très proche comme distance "infinitésimale", mais ça ne marche pas en général pour un objet distant, car si la métrique évolue pendant le temps d'aller retour, il est illicite de penser que l'évènement "écho" de B s'est produit simultanément avec la date pile entre le départ et l'arrivée du signal, parce que l'aller et le retour n'ont aucune raison d'avoir la même "durée" Si on renvoie maintenant le signal reçu d'un quasar distant vers le quasar et qu'on attend qu'il reçoive l'écho , ça mettra bien plus de temps au retour qu'à l'aller : la distance mesurée comme ça n'a donc aucun sens , par exemple tu ne peux pas l'obtenir comme l'intégration d'une distance infinitésimale ∫dl

[Archi3]

Mais bon le problème ne se pose pas dans les coordonnées de Rindler, car la métrique est indépendante du temps, et donc la distance radar comme tu l'as bien définie est bien la distance propre au sens d'une distance mesurée par une règle physique qui serait déplacée d'un observateur A à un observateur B coïncidant avec l'évènement et immobile en coordonnées de Rindler.

[mach3]

Alors voilà... pour obtenir ce que tu dis pour la trajectoire de l'accéléré dans son repère de KM je dois prendre (avec x et t coordonnées en Minko) :

et non pas

et non pas

Et ça ne garantit rien sur tout le reste ! Comprend pô...

Merci

je crois que j'ai trouvé le problème, on en reparle plus tard, pas le temps ce matin.

m@ch3

[Zefram Cochrane]

Mais bon le problème ne se pose pas dans les coordonnées de Rindler, car la métrique est indépendante du temps, et donc la distance radar comme tu l'as bien définie est bien la distance propre au sens d'une distance mesurée par une règle physique qui serait déplacée d'un observateur A à un observateur B coïncidant avec l'évènement et immobile en coordonnées de Rindler.

Bonjour,
C'est faux :
Salut
Sur ce schéma , la distance propre entre Rouge et Bleu est de 15 s.l; la distance radar entre Rouge et Bleu est de 10.4s.l pour Rouge et de 16.48s.l pour Bleu.


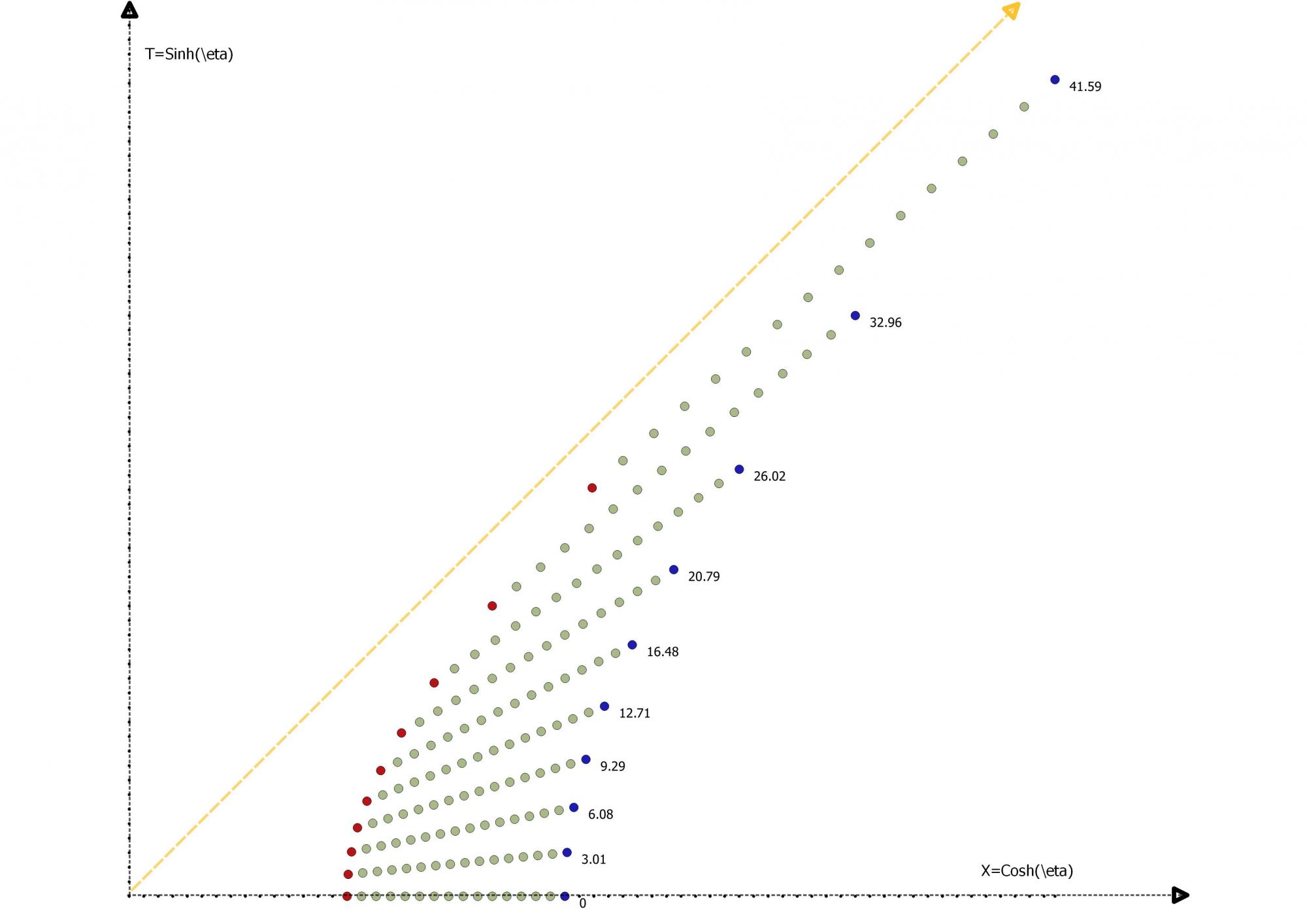
On voit nettement sur ce schéma que le nombre de capsules reste identique. Donc si on considère que la longueur unitaire de la règle correspond au diamètre d'une capsule la longueur de la règle (longueur propre) restera invariant.

[Archi3]

Bonjour,
C'est faux :
Salut
Sur ce schéma , la distance propre entre Rouge et Bleu est de 15 s.l; la distance radar entre Rouge et Bleu est de 10.4s.l pour Rouge et de 16.48s.l pour Bleu.

donc ton calcul est probablement faux.