Intégration, c'est quoi exactement ?

[marc.suisse]

Bonjour Messieurs !!

Je suis en train de suivre un cours ici sur le forum électronique sur une alimentation .

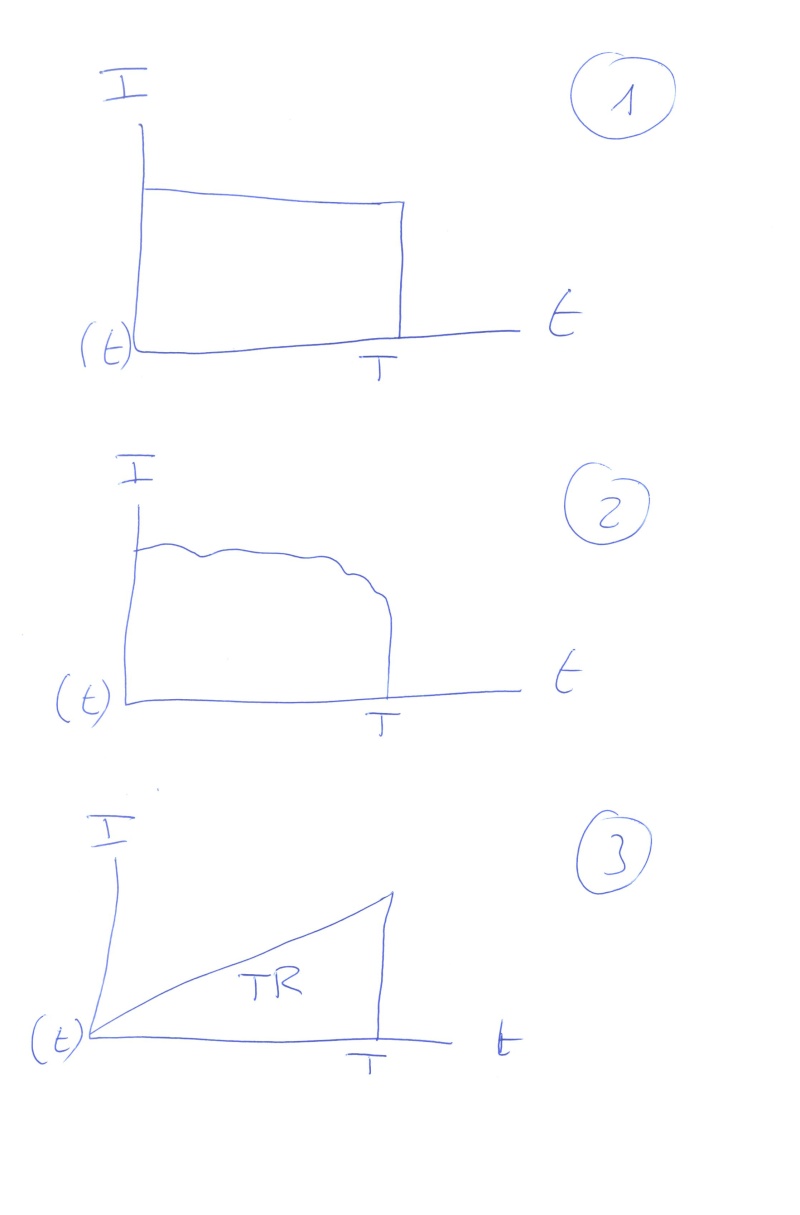
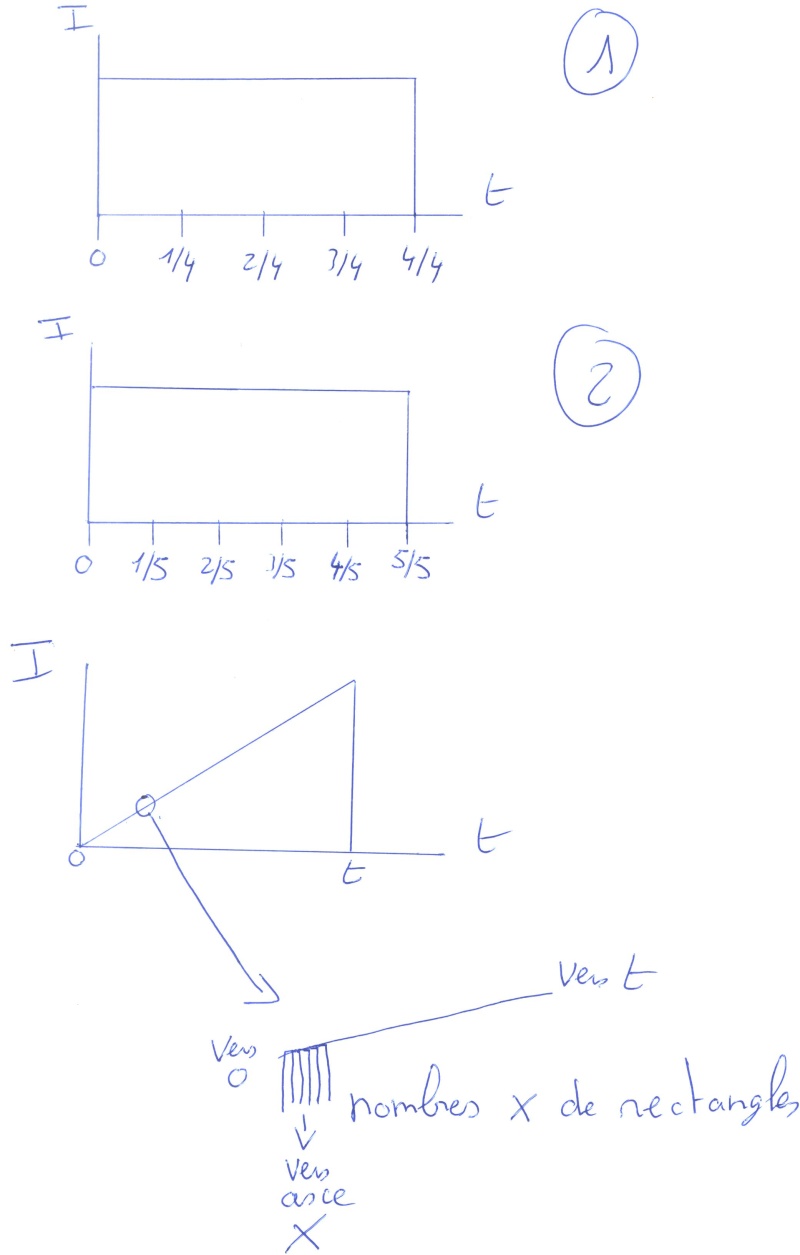
Dans les calculs , vient assez souvent le terme d'intégration

T
∫
0

Mais après fais quelques recherches sur internet et sur wikipédia , je ne trouve rien comme explication "simple" .

Dans quel but et à quoi sert une intégration , est-ce comme son nom l'indique de fusioner 2 formules ensemble ?
-----

[invite88ef51f0]

Salut,
Sais-tu ce qu'est une dérivée ? une primitive ?

[marc.suisse]

Salut et merci de ta réponse !!

Hum , alors je vais faire simple , je suis absolument novice en mathématique , donc non je ne sais pas ce qu'est une primitive et une dérivée .

Très mal partis dirait-on

[invite4b0d57b6]

Salut !
Quel niveau as-tu exactement en maths ? ^^

[A voir en vidéo sur Futura]

[invite88ef51f0]

Quel est ton niveau en maths ?
Si je te parle de fonction, ça va ?

[invite6909706f]

Salut,

Je ne pense pas que tu puisses calculer une intégrale sans des notions de derivés. Il n'existe donc d'explication "simple" pour les intégrations.

Si tu as besoin de savoir calculer les intégrales, étudie d'abord tout ce qui conserne les derivés, et après tu pourras te lancer dans le calcul d'intégral...

Bonne chance

[marc.suisse]

Salut et merci de vos réponses !!

Quel est ton niveau en maths ?
Si je te parle de fonction, ça va ?

Mon niveau est pour dire insignifiant , non sérieux je n'y connais rien , juste les math apris à l'école c'est tout .

Donc pour les fonctions , ben non ca vas pas

Je ne pense pas que tu puisses calculer une intégrale sans des notions de derivés. Il n'existe donc d'explication "simple" pour les intégrations.

Si tu as besoin de savoir calculer les intégrales, étudie d'abord tout ce qui conserne les derivés, et après tu pourras te lancer dans le calcul d'intégral...

Je suis tout à fais d'accord , je sens que j'ai du boulot pour apprendre tout ça .

[invite35452583]

Bonjour,
je vais essayer de rester dans le domaine initial : l'électronique, enfin surtout l'électricité.
Une capacité emmagasine une certaine quantité de charge électrique entre un temps t=0 et un temps t=T.
Si l'intensité électrique qui l'alimente est constante I, on a :
Q(t=T)-Q(t=0)=I.T ce qui correspond à l'aire d'un rectangle de largeur T et de hauteur I.
Maintenant si I varie en fonction du temps i(t), quel est la charge emmagasinée ?
Prenons un autre cas simple, i(t)=c.t où c est une constante. Graphiquement la courbe de i est une droite du plan repéré par les coordonnées (t,i). La charge emmagasinée est l'aire de la zone comprise entre cette droite, l'axe (Ox) et les droites verticales t=0 et t=T (l'aire d'un triangle Tr). Pourquoi ? Découpons l'intervalle en t [0;T] en de petits intervalles [(k/N)T ; ((k+1)/N)T], sur ces petits intervalles i est presque constant et compris entre c(k/n)T et c((k+1)/N)T la charge emmagasinée entre (k/N)T et ((k+1)/N)T (durée=T/N) est comprise entre [c(k/N)T](T/N) et [c((k+1)/N)T](T/N). Graphiquement on voit que ceci correspond à l'aire de deux petits rectangles de hauteur c(k/n)T pour l'un et c((k+1)/N)T pour l'autre. La somme de toutes ces petites aires vaut approximativement l'aire définie par le triangle initial Tr, l'approximation est d'autant meilleure que N est grand. Et on a une égalité stricte si on fait tendre N vers +infini. On a donc dans ce Q(t=T)-Q(t=0)=cT²/2
D'une manière générale, l'intensité i varie en fonction du temps et est une fonction t->i(t). La charge emmagasinée entre t=0 et t=T est la somme de petits rectangles de largeur infintésimalement petite et de hauteur i(t) (même type de découpe que précédemment) et finalement Q(t=T)-Q(t=0)= aire comprise entre la courbe, l'axe (Ox), et les verticales t=0 et t=T. En faisant attention, à la position de la courbe par rapport à (OX), si la courbe est placée en dessous i<0 et c'est une charge négative qui est emmagasinée, si la courbe est au-dessus la charge emmagasinée est positive. Si la courbe passe alternativement en-dessous et au-dessus de (Ox) il y a des phases de chargement positif et des phases de chargeent négatif, il faut prendre les aires avec les signes correspondants. ceci est une première difficulté, plus "psychologique" qu'autre chose : des aires négatives peuvent surprendre mais dans cet exemple c'est, il me semble, assez compréhensible.
L'autre difficulté, technique celle-ci, est le calcul de cette aire. Pour les deux premiers exemples, un rectangle et un triangle, le calcul de l'aire est facile mais d'une manière générale comment calculer cette aire ? Et là va se clore cette tentative d''explication simple car la notion de dérivée va intervenir.

En espérant que cela t'aide à commencer à y voir un peu plus clair.

[marc.suisse]

Salut Homotopie et merci beaucoup d'avoir pris le temps d'écrire cette explication .

Je sens que je vais devoir la prendre en petit morceaux pour la rendre plus digeste .

j'ai fais 3 petits graphique correspondant aux premières choses que tu m'as expliqué , dis moi stp si j'ai bien compris

Une capacité emmagasine une certaine quantité de charge électrique entre un temps t=0 et un temps t=T.
Si l'intensité électrique qui l'alimente est constante I, on a :
Q(t=T)-Q(t=0)=I.T ce qui correspond à l'aire d'un rectangle de largeur T et de hauteur I.

=1

Maintenant si I varie en fonction du temps i(t), quel est la charge emmagasinée ?

=2

Maintenant si I varie en fonction du temps i(t), quel est la charge emmagasinée ?
Prenons un autre cas simple, i(t)=c.t où c est une constante. Graphiquement la courbe de i est une droite du plan repéré par les coordonnées (t,i). La charge emmagasinée est l'aire de la zone comprise entre cette droite, l'axe (Ox) et les droites verticales t=0 et t=T (l'aire d'un triangle Tr).

=3



Si je comprends bien , i(t) est une fonction ?

Merci encore de ton aide !!

[invite35452583]

Bonsoir,
les dessins corespondent bien en effet. Il semblerait donc que tu as bien compris les grandes lignes.

[invite7553e94d]

Bonsoir.

Si je peux me permettre d'ajouter quelques détails sans trop surcharger. Homotopie a donné une définition intuitive de l'intégrale, mais il faut savoir qu'elle est relativement proche de l'intégrale de Riemann.

Riemann est un mathématicien du XIX^e siècle. Parmi ses travaux, on retrouve la construction de l'intégrale comme limite d'une somme. Ce terme barbare n'est autre que ce qu'a expliqué homotopie : on considère la fonction (par exemple l'intensité dans le temps) constante sur de petits intervalles de temps, puis on regarde ce qu'il se passe quand ces intervalles sont de plus en plus petit.

Ensuite, Riemann démontre qu'il est possible de calculer des intégrales de manière assez simple (selon les intégrales bien sûr).

Quelques exemples simples :

• Lorsque que l'intensité est constante (égale à i₀) :
  
• Lorsque que l'intensité est proportionnelle au temps écoulé (au début elle vaut i₀ puis augmente de k ampères toutes les secondes) :
  

(note : ne pas se soucier du dt)

Ensuite, si tu as besoin de calculer des intégrales, je te conseille : soit une calculatrice étant capable de le faire, soit ce site : http://integrals.wolfram.com/index.jsp
Si tu choisis la seconde solution, il te faudra apprendre leur syntaxe, utiliser comme variable x (au lieu de t) ; et pour avoir ton résultat numérique, tu remplaces x par ton temps de fin d'une part, par ton temps de début d'autre part, puis tu soustrait les deux résultats.

Bonne chance pour la suite.

[invite1ea97de8]

Petite correction pour le dernier message. C'est pas une intégrale de Riemman mais une somme de Riemman. L'idée c'est de se dire, si je prend un mini morceau de courbe par exemple, ben s'il est assez petit mon morceau, ben j'aurai une droite entre ses deux extrémétié. Idem pour le morceau qui le suit, et petit a petit, si je somme tous les petits morceau, je fais une somme de Riemman, qui lorsque la dimension des petits morceaux tend vers zéro ( la fameuse limite de la dérivé) bien j'arrive a passé d'une somme, qui en passant serait impossible a calculer terme a terme, à une intégrale.

Une intégrale c'est l'air sous une courbe, pour faire simple

[marc.suisse]

Bonjour Messieurs et encore merci de vos réponses !!

Je sens que je vais passer du temps à comprendre tout ça

Une question :

prgasp dit :

Lorsque que l'intensité est proportionnelle au temps écoulé (au début elle vaut i0 puis augmente de k ampères toutes les secondes) :

Je retrouve ce qu' homotopie disait :

Découpons l'intervalle en t [0;T] en de petits intervalles [(k/N)T ; ((k+1)/N)T], sur ces petits intervalles i est presque constant et compris entre c(k/n)T et c((k+1)/N)T la charge emmagasinée entre (k/N)T et ((k+1)/N)T (durée=T/N) est comprise entre [c(k/N)T](T/N) et [c((k+1)/N)T](T/N).

Donc K est un endroit sur l'axe horizontale X , c'est bien ça ?

Mais que veux-dire k+1)/N)T ? J'ai un peu de peine à saisir....

Homotopie me parle aussi de ça :

l'axe (Ox)

C'est en fait l'axe horizontale , c'est à dire l'abcisse ?

[invite7553e94d]

Donc K est un endroit sur l'axe horizontale X , c'est bien ça ?

Arf, mille pardon il y a confusion : ce n'est pas le même k (celui d'homotopie peut être représenté sur l'axe des abscisses, pas le mien.

Mais que veux-dire k+1)/N)T ? J'ai un peu de peine à saisir.

Pour comprends mieux vaut faire un dessin : découpe un intervalle [0;T] en 4, tu as
[0;(1/4)T[, [(1/4)T;(2/4)T[, [(2/4)T;(3/4)T[, [(3/4)T;(4/4)T].

Si tu découpes en 5 tu as
[0;(1/5)T[, [(1/5)T;(2/5)T[, [(2/5)T;(3/5)T[, [(3/5)T;(4/5)T[, [(4/5)T;(5/5)T].

Si tu découpes en N tu as [0; (1/N)T[, [0; (2/N)T[, ... [(k/N)T, (k+1/N)T[, [(k+1/N)T, (k+2/N)T[, ... [(N-1/N)T; T].

C'est en fait l'axe horizontale , c'est à dire l'abcisse ?

Ouep !

Petite correction pour le dernier message. C'est pas une intégrale de Riemman mais une somme de Riemman.

Non non, je parle bien d'intégrale de Riemann (j'en ai la construction sous les yeux).

[invite9c9b9968]

Vous avez tous les deux raison : l'intégrale de Riemann peut se concevoir comme la limite d'une somme de Riemann

[invite6de5f0ac]

Bonjour,

Tout cela est bel et bon, mais je m'étonne que personne n'ait mentionné que l'intégrale depuis x₀ jusqu'à x₁ de f(x)dx (eh non, je ne me débrouille toujours pas avec LaTeX) n'est rien d'autre que la surface délimitée par:

• l'axe des abscisses,
• la droite verticale x = x₀ ,
• la droite verticale x = x₁ ,
• la courbe représentative de f, soit y = f(x).

Après, qu'on calcule ça comme une intégrale (ou une somme) de Riemann, ou une intégrale de Lebesgue, c'est juste une question de formalisation. Mais l'interprétation est toujours la même...

-- françois

[invite7553e94d]

Vous avez tous les deux raison : l'intégrale de Riemann peut se concevoir comme la limite d'une somme de Riemann

...
La somme de Riemann n'est définie que pour construire son intégrale non ?

[marc.suisse]

Bonsoir Messieurs !!

J'avance par petits pas , mais j'avance quand même .

Je compte d'ailleurs sur votre patience

Selon prgasp77 :

Pour comprends mieux vaut faire un dessin : découpe un intervalle [0;T] en 4, tu as
[0;(1/4)T[, [(1/4)T;(2/4)T[, [(2/4)T;(3/4)T[, [(3/4)T;(4/4)T].

Si tu découpes en 5 tu as
[0;(1/5)T[, [(1/5)T;(2/5)T[, [(2/5)T;(3/5)T[, [(3/5)T;(4/5)T[, [(4/5)T;(5/5)T].

= 1 et 2



Mes dessins tiennent la route ?

Ensuite j'ai dessiné un schéma qui exprime ce que j'ai compris pour calculer l'air , c'est à dire que vu qu'on ne peut pas directement calculer l'aire totale de sous la courbe , on prends x nombres de petits rectangle qui leurs sommes équivaudra l'aire totale .

J'ai toujours bon ?

Par contre je n'ai toujours pas compris ceci :

Si tu découpes en N tu as [0; (1/N)T[, [0; (2/N)T[, ... [(k/N)T, (k+1/N)T[, [(k+1/N)T, (k+2/N)T[, ... [(N-1/N)T; T].

Pour les 2 premiers

[0; (1/N)T[, [0; (2/N)T

Je comprends que c'est la distance entre 0 et 1/N pour le premier et la distance entre 0 et 2/N pour le deuxième .

Par contre pour ceux-ci :

[(k/N)T, (k+1/N)T[, [(k+1/N)T, (k+2/N)T[, ... [(N-1/N)T; T].

Que vient le k là dedans , est-ce une inconnue ? Comme en algèbre ou on utilise le termer "x" ?

Je comprends pas très bien , surtout que tu n'as pas mis les points virgules comme sur les premiers exemples .

Encore merci de votre aide , c'est sympa

[invite7553e94d]

Salut.
Oui, tes dessins tiennent la route (il semble que tu ais compris le truc

Par contre pour ceux-ci :

[(k/N)T, (k+1/N)T[, [(k+1/N)T, (k+2/N)T[, ... [(N-1/N)T; T].

Que vient le k là dedans , est-ce une inconnue ? Comme en algèbre ou on utilise le termer "x" ?

Je comprends pas très bien , surtout que tu n'as pas mis les points virgules comme sur les premiers exemples .

Encore merci de votre aide , c'est sympa

Le k est ici, un compteur (on parle de variable muette), il prend tour à tour toutes les valeurs possible et ainsi décrit tous les intervalles possibles.
Mais peu importe, c'est un détail (pour les point-virgules : erreur de ma part).

[marc.suisse]

Salut et encore merci de ta réponse !!

Le k est ici, un compteur (on parle de variable muette), il prend tour à tour toutes les valeurs possible et ainsi décrit tous les intervalles possibles.

Cela veut dire qu'il peut en avoir énormément ?

Par contre pas à l'infini , sinon on ne pourrait plus calculer l'aire non ?

[invite7553e94d]

Justement, le calcul intégral permet de faire le calcul pour un nombre infinit d'intervalles infiniment petits ... En découpant ton aire en rectangle, tu approches la solution (plus tu découpes en un nombre grand d'intervalles, plus ton résultat est proche de l'aire réelle).

Et ce qui est génial, c'est qu'il est même possible de calculer l'erreur maximale que tu commets, donc d'avoir un résultat aussi proche que l'on veut de la solution réele (un dessin pour m'expliquer) :



Nous savons que l'air réelle sous la courbe vaut :


Nous avons découpé notre intervalle [a;b] en 10 intervalles :
, , , ... ,
Nous savons que l'aire sous la courbe est inférieur à l'air en rouge qui vaut :

Nous savons que l'aire sous la courbe est supérieure à l'air en bleu qui vaut :


Nous avons donc :

L'erreur maximale comise en prenant ou pour valeur de l'aire réelle est, au plus, de
(car les termes de A et de B se simplifient par eux même (le second de A est le premier de B, le troisième de A est le second de B ... etc., à la fin ne reste plus que le premier de A et le dernier de B).


Ainsi, si tu souhaites avoir un résultat avec une précision inférieure à , alors la découpe de ton intervalle en 10 est correct, sinon il faut découper en plus que 10 (il est même possible, à partir d'une précision minimale donnée de calculer en combien d'intervalles il faut découper )

Attention, les résultats obtenus ici ne sont pas valables pour toutes les fonctions (croissantes notamment).

J'espère que je me suis expliqué clairement, j'ai tendance à m'emballer

[marc.suisse]

Hello !!

Merci beaucoup pour cette réponse

Excuses du retard de la réponse , mais week-end prolongé oblige

Il y a une chose que je ne comprends pas , quand tu parles de l'air sous la courbe qui est plus petite à l'air en rouge , pour calculer ceci , j'ai bien compris que pour calculer l'air du premier rectangle , tu multipliais la hauteur ( f ) avec la largeur ( b-a/10 ) , mais le deuxième , pourquoi tu ne gardes pas le ( b-a/10 ) pour la largeur et de prendre la valeur de ( f ) pour la hauteur correspondant au deuxième rectangle ?

Autre chose , le DT dans la première formule , il veut dire quoi ? Je dois également le laisser de côté comme sur les autres posts ?

Dernière question , tu fais comment pour écrire les formules ici sur le forum ?

Et le dessin , tu le fais avec quel programme ?

excuses moi de t'innonder de questions

[invite7553e94d]

Hello !! Merci beaucoup pour cette réponse
Excuses du retard de la réponse , mais week-end prolongé oblige

Maid de rien, c'est un vrai plaisir. Et je reviens moi aussi de week-end

Il y a une chose que je ne comprends pas , quand tu parles de l'air sous la courbe qui est plus petite à l'air en rouge , pour calculer ceci , j'ai bien compris que pour calculer l'air du premier rectangle , tu multipliais la hauteur ( f ) avec la largeur ( b-a/10 ) , mais le deuxième , pourquoi tu ne gardes pas le ( b-a/10 ) pour la largeur et de prendre la valeur de ( f ) pour la hauteur correspondant au deuxième rectangle ?

Erf ... j'ai un peu de mal à comprendre la question, alors pour être sûr d'y répondre je vais voir large.
Pour le calcul de l'air en rouge, A₁₀, je somme les aires des dix rectangles en rouge (délimités de vert et de noir).
Le premier rectangle rouge (tout à gauche) a pour largeur et pour hauteur la valeur de ma fonction au point d'abscisse (premier trait vert).
Le second rectangle rouge a la même largeur (), mais sa hauteur est différente, c'est la valeur de la fonction au point d'abscisse . etc.

Pour l'air en bleu, je procède de même à la différence près que je prends pour hauteur des rectangle la valeur de ma fonction (c'est la mienne pas touche !) à droite du rectangle, et pas à gauche comme pour l'air en rouge Et pourquoi je fais ça ? Et bien parce que sinon les deux airs seraient égales Et en plus, comme ça j'encadre mon aire réelle.[/QUOTE]

Autre chose , le DT dans la première formule , il veut dire quoi ? Je dois également le laisser de côté comme sur les autres posts ?

Pas tout à fait. Le (en minuscule stp) exprime la "largeur" d'un intervalle infiniment petit ; je m'explique.
Je t'avais expliqué que le calcul intégral est en réalité l'étude précédente mais en considérant un nombre infini d'intervalles de plus en plus petits. Dans notre cas, pour calculer notre aire nous sommons les 10 aires qui valent largeur hauteur (hauteur : valeur de la fonction).
Et bien pour les intégrales, c'est kif-kif
est un S (comme somme) : nous sommons un très grand nombre (en fait infini) de termes, mais nous sommons.
: hauteur de la fonction en un point
(en minuscule stp) : ("largeur" de l'intervalle)

tu fais comment pour écrire les formules ici sur le forum ?

Grâce à . Va faire un tour du coté des annonces officielles (premier forum)

Et le dessin , tu le fais avec quel programme ?

Avec PhotoShop + ImageReady (Tu peux faure de même avec Gimp qui est un logiciel gratuit).

Bonne soirée.

[marc.suisse]

Hello !!

Je commence à y voir un peu plus clair , tu réponds très bien à ma question très vague lol .

Je vais encore lire et je te redis .

Franchement c'est cool de prendre du temps pour expliquer tout ceci à un ignare comme moi mdr .

A propos , tu as appris ça ou ? Je ne sais pas si tu as remarqué , mais je suis très curieux

[invite7553e94d]

A propos , tu as appris ça ou ? Je ne sais pas si tu as remarqué , mais je suis très curieux

Justement parce que je suis très curieux moi aussi J'ai appris tout cela en classe de terminale scientifique. L'analyse de fonction est un ensemble d'outils très puissants, ils permettent de travailler avec des relations complexes en ne calculant que très peu. Deplus, il y a peu à apprendre (mais beaucoup à pratiquer).

Si tu le souhaites, je peux te mettre mes cours d'analyse (formalisation des programmes de 1ère et Tale S), il est dense mais bon.

[marc.suisse]

Hello , tu vas bien ??

Ce qui m'embête , c'est que je suis curieux , mais j'ai de la difficulté à comprendre certaines choses , tu sais j'ai envie de comprendre , mais ca bloque , c'est emmerdant

J'ai une petite question , supposons que j'ai une courbe et que j'aimerais calculer son aire , donc comme ta courbe avec les rectangles bleu et rouge .

En premier lieu , je dois quand même pas dessiner des petits rectangle comme tu l'as fais ? Tout ceci se fait par calcul non ?

Ensuite , le dt ( en minuscule ok ) , c'est en fait dans notre cas b-a/10 ?

[invite7553e94d]

En premier lieu , je dois quand même pas dessiner des petits rectangle comme tu l'as fais ? Tout ceci se fait par calcul non ?

Non, inutilé une fois que tu as compris le truc, tu fais ta somme sans avoir à apsser par les rectangles. Mais le soucis, c'est que pour avoir une valeur assez précise, il faut découper en un très grand nombre de rectangle, donc faire une somme avec un très grand nombre de termes ... ce qui est difficile sans machine

C'est pour cela qu'on a inventé le calcul intégral, pour éviter de faire des sommes monstruseuses (et pour avoir un résultat exact).

Ensuite , le dt ( en minuscule ok ) , c'est en fait dans notre cas b-a/10 ?

[marc.suisse]

Salut et franchement encore merci de tes réponses !!

Tu aurais par hasard un exemple d'exercice sur tout ce qu'on à vu ?

J'ai quand envie de passer à la pratique .


Mais n'empêche , j'aimerais bien comprendre comment tu ddécoupes en x nombre de rectangle sans les dessiner ...