DM de maths. TS spé maths.. MERCI
Bonsoir à tous j'ai vraiment un grand besoin d'aide pour faire cette exercice. je suis actuellement en TS spé maths, et voici mon Dm..
Mais attention je ne veux aucune réponse svp. Juste quelque piste pour me mêttre sur la bonne voie.. Merci beaucoup pour l'aide apporté..
Voici l'énoncé:
A) Première partie entièrement réaliser.
B) Volume du cône :
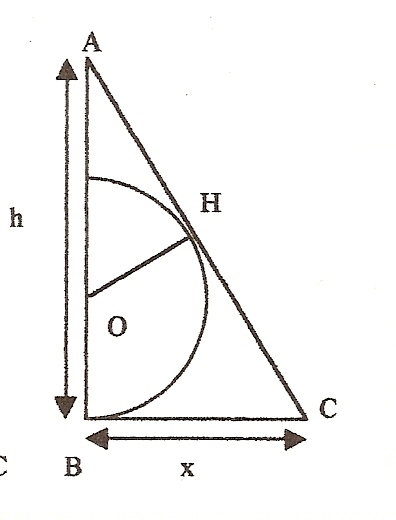
Dans la figure ci-contre : le triangle ABC est rectangle en B, le demi-cercle de centre O a pour rayon 1, la droite (BC) est tangente en B au demi-cercle, la droite (AC) est tangente en H au demi-cercle. On pose AB=h, BC=x (avec x>1).
1°) Prouver que OH/AH=BC/AB . En déduire les égalités: h = x[racine(h-1)²-1] ; x² =h/h-2 ; h =2x²/x²-1
2°) Pappelons que le volume d'un cône de révolution de hauteur h et de base circulaire d'aire S est V =hS/3 . En pivotant autour de (AB), le triangle ABC engendre un cône de révolution de sommet A.
a. Exprimer le volume V(x) du cône en fonction de x.
b. A l'aide des résultats de la partie A), déterminer le volume minimal de ce cône; donner alors la cette valeur de l'angle BÂC (à 0.1° près)
-----