Théorie des graphes

[invitea35bb224]

Bonjour à tous
Dans le cadre de mes TIPE, je me retrouve face à un problème qui me dépasse, voici son énoncé:

Soit un graphe composé de N+1 sommet dont un sommet D et N sommets Xi
Le problème est soumis aux condition suivantes:
- Chaque sommet Xi doit être relié par 2 arcs (et seulement 2 arcs)
- Le sommet D doit être relié aux sommets Xi par 2M arcs
- Chaque cycle du graphe doit inclure D
Quel est le nombre d'arcs joignant les sommets Xi entre eux?

Je pense que la réponse est N-M mais pas moyen de le prouver rigoureusement...

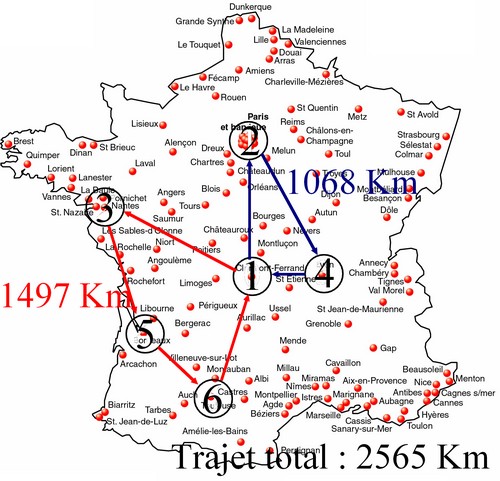
Voici une petite illustration (parce que je sais pas si je suis clair) dans le cas N=5 et M=2:
Pièce jointe 179310
Attention, cette image ne représent pas le problème mais un graphe construit selon les conditions de l'énoncé
Et on trouve bien là N-M=3 jonctions entre les Xi (mais on ne sait pas si cette réponse est valable pour toutes les configuratiion de ce problème)

Voila, votre aide me serait très précieuse
Merci d'avance
-----

[thepasboss]

bonsoir,

tu as raison pour ton hypothèse. Pour le prouver, je vois une méthode pas mal :

On prend les points X_i seuls, et on cherche les graphes entre ces points tels que de chaque Xi partent deux arcs. On remarque alors que le graphe se décompose en cycles disjoints (pour le prouver on peut considérer la relation d'équivalence "Xi et Xj sont équivalents si et seulement si ils sont relié par une série d'arcs").

Or si on considère un graphe cyclique passant par k sommets, ce graphe a k arrêtes. Donc en tout il y a N arrête dans notre graphe. Maintenant si on ajoute un point D au bazar, comment transformer le graphe pour qu'il colle aux hypothèses ? Je te laisse voir qu'il suffit alors de choisir une arrête et une seule dans chaque cycle, et de la tordre pour la faire passer par D... Donc si on note M le nombre de cycle, les arrêtes entre les Xi sont au nombre de N - "le nombre d'arrêtes qu'on a tordu pour les faire passer par D", et ce dernier nombre vaut M...

Voilà voilà

[thepasboss]

il faut un peu corriger ce que je raconte, au final si on prend les hypothèses telles quel, on se moque de prendre un et un seul arc dans chaque cycle.

[invitea35bb224]

Merci pour ta réponse claire et très rapide
Content de voir que mon hypothèse est bonne, ça confirme pas mal de chose pour mes TIPE
Merci et bonne journée à toi

[A voir en vidéo sur Futura]

[thepasboss]

Au fait une petite question,

c'est pour quoi exactement ce machin ? Parce que c'est rigolo ^^

[invitea35bb224]

C'est dans le cadre du problème de la tournée de véhicule (VRP)
En fait t'as un dépot D où est entreposé M véhicule et tu as N clients
Il faut livrer tous les clients sous les conditions suivantes
- Chaque client Xi doit être livrer par une quantité di de marchandise (sachant que chaque véhicule possède la même capacité C, il ne faut pas que la demande en marchandise des clients livrés par un véhicule dépasse C)
- Tous les clients doivent être livrés, et ce une seule et unique fois (donc par un seul véhicule)
- Chaque cycle commence et se termine au dépot
Et le but est de déterminer le parcours des véhicules de tel sorte à ce que la somme de leurs trajets soit minimal

Voici un petit exemple de résolution d'un VRP:


Donc en gros pour résoudre ce problème tu as les méthodes de résolution approchées, qui sont assez rapides et qui offrent une bonne solution bien que non optimale
Et tu as les méthode de résolution exactes, plus lentes mais qui offrent le meilleur résultat
Je m'interesse à ces dernières, et comme les méthodes de résolution exactes dévellopées aujourd'hui sont absolument imbitables, j'ai créer mon propre algorithme
Et une partie de cet algorithme est basée sur l'hypothèse qu'il y a N-M jonctions entre les clients
Voila ^^

[JPL]

Rappel de la charte du forum :

Ne vous appropriez pas les informations d'autrui, citez vos sources.

Donc donne le lien vers la page qui héberge la carte, ou bien donne la source si ce n'est pas sur internet.

[invitea35bb224]

Ben la source c'est moi vu que j'ai moi même résolu ce problème et créé cette carte