Regression lineaire minimisant l'erreur relative

[invite6ee92c43]

Bonjour

je dois calibrer un signal de débitmètre sorte que le débit obtenu aient une erreur de 1% maximum.

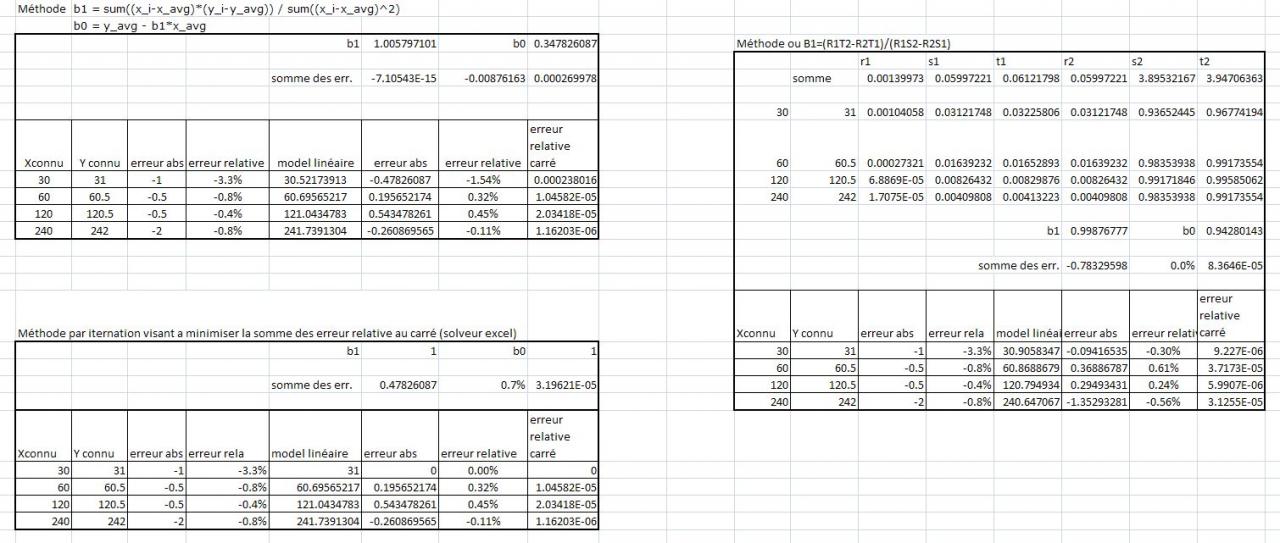
Jusqu’à présent j'utilise une régression linéaire par la méthode des moindres carrés, soit

y = b1*x + b0
b1 = sum((x_i-x_avg)*(y_i-y_avg)) / sum((x_i-x_avg)^2)
b0 = y_avg - b1*x_avg

cet méthode permet de minimiser les écarts absolus. or dans mon application ça cause problème car si j'ai un série de valeur comme suit

Xconnu Y connu erreur abs erreur relative model linéaire* erreur abs erreur relative
30 31 -1 -3,3% 30,31304348 -0,686956522 -2,2%
60 60 0 0,0% 60,5173913 0,517391304 0,9%
120 120,5 -0,5 -0,4% 120,926087 0,426086957 0,4%
240 242 -2 -0,8% 241,7434783 -0,256521739 -0,1%

* model linéaire selon la méthode des moindres carrés soit y = 1,006811594 x + 0,108695652.

mon problème est que ce model me donne un erreur relative après l'application du model linéaire de plus de 1% pour la le couple 30,31. car son poids dans la méthode des moindres carrés est 2 fois moins important que l'erreur du couple 240,242.

Comment effectuer une régression qui viserais à minimiser l'erreur relative?

Merci de votre aide
-----

[invite63e767fa]

Bonjour,

S'il y a n mesures (xi, yi), il y a n erreurs relatives généralement différentes les unes des autres.
Lorsque tu écris << Regression lineaire minimisant l'erreur relative >> de laquelle d'entre elles parles-tu ?
Je suppose que tu voulais dire "minimisant la moyenne des erreurs relatives".
Ou encore plus vraissemblablement "minimisant la moyenne des carrés des erreurs relatives" puisque tu indiques par ailleurs que tu souhaites utiliser la méthode des moindres carrés.
Si c'est bien cela, le calcul est indiqué en page jointe.

Les principes de résolution relatifs à ce genre de problèmes sont données dans de très nombreux ouvrages de statistiques.
Voir par exemple l'article : "régressions coniques, quadriques, circulaire, sphérique, linéaires et apparentées"
http://www.scribd.com/JJacquelin/documents

[invite63e767fa]

Remarque: En affectant des poids w_i à chaque point avec w_i=abs(1/y_i) et avec les formules classiques de régression par les moindres carrés, le résultat serait exactement le même qu'avec les formules données dans le mail précédent.

[invite094d8e48]

Bonjour JJacquelin,

Est ce que votre démonstration sur la régression linéaire peut s'appliquer à d'autres régressions ?
Dans mon travail j'ai comme projet de faire un PIC (plan industriel et commercial) et qui demande au préalable de calculer un prévisionnel par produit en fonction de son historique.
J'aurais besoin de faire plusieurs régressions :
* constante [y=Cte]
* droite [y=a.x+b]
* parabole [y=a.x^2+b.x+c]
* polynome de degre 3 [y=a.x^3+b.x^3+c.x+d]
* exponentielle [y=a.e^(b.x)+c]
* logarithme neperien [y=a.ln(x+b)+c]
* hyperbole [y=a/(x+b)+c]
* sinusoide [y=A.sin(w.x+phi)+k]
* exponentielle (pente a l'origine seule degre de liberte) [y=50* (1-e^(-alpha.x))]
* puissance [y=K.x^alpha]
* droite passant par l'origine [y=a.x]
* loi Gaussienne (ou loi normale) [y=LoiGaussienne(m,s)]

Puis de regarder le coeff. de régression le plus proche de 1 pour trouver la meilleure régression.

Cependant je ne trouve pas de formule toute faite pour chacune des régressions.
Si je reprends ta démo puis je arriver à des résultats similaire pour les autres régressions.

Ou alors existe t'il des sites qui donne les formules ou démonstration ?

Merci d'avance

[A voir en vidéo sur Futura]

[invite63e767fa]

La plupart de ces cas sont traités dans l'article déjà cité :
"régressions coniques, quadriques, circulaire, sphérique, linéaires et apparentées"
http://www.scribd.com/JJacquelin/documents
Et avec le principe général qui est indiqué, on traite beaucoup d'autres cas.

[invite63e767fa]

Certaines fonctions faisant intervenir de façon non linéaire des paramètres à optimiser sont plus difficiles à traiter,
par exemple le paramètre b dans le cas y=a.ln(x+b)+c, ou par exemple les paramètres w et phi dans y=A.sin(w.x+phi)+k ).
Il existe des méthodes par calcul numérique récursif. Ces méthodes sont expliquées dans les ouvrages de statistiques et sont implémentées dans les logiciels commerciaux.
Remarque : Certains de ces cas sont traités de façon non récursive par une autre méthode, dans l'article
"Régressions et équations intégrales"
www.scribd.com/JJacquelin/documents

Pour un usage industriel ou commercial, je vous conseille plutôt de vous orienter vers des logiciels professionnels existants. Une recherche sur le web devrait vous apporter les documents publicitaires correspondants.

[invite094d8e48]

Merci beaucoup JJacquelin,

je trouve vos articles excellents.

Merci encore, même si mon niveau en math est un peu limite, je pense tout de même pouvoir m'en sortir.

Encore merci

[invite6ee92c43]

Merci JJaquelin

j'ai utilisé la méthode que vous suggérer et voici les résultats



toutefois vous remarquerez que la méthode du solveur excel donne un meilleur résultats, pourquoi?

Merci encore

[invite63e767fa]

Bonjour,

je regrette, je n'ai pas le temps de refaire vos calculs numériques pour vérifier.
Toutefois, il semble que les résultats donnés par Excel après itérations n'aient pas été bien retranscrits pour le calcul des erreurs relatives. Il semble y avoir une incohérence dans le tableau que vous avez transmis (voir page jointe).
Désolé, je ne peux pas consacrer plus de temps à cette question.
Bonne continuation.
JJ.

[invite6ee92c43]

Bonjour JJacquelin

Merci beaucoup, effectivement il y avait une erreur dans l'exemple que j'ai fourni et en corrigeant cet erreur le méthode que vous propose est la plus exacte.

Merci encore une fois