Graphe : arbre couvrant "maximum"

[Anakinele]

Bonjour,

Dit simplement, mon problème est de relier un ensemble de points du plan entre eux sans jamais former de cycles.
Après quelques recherches et avec un vocabulaire plus mathématique, j'ai trouvé la solution consistant à déterminer un arbre couvrant pour mon graphe et, en particulier, l'arbre (un arbre ?) couvrant minimum., cf. l'image suivante :

min_spanning_tree.png

Mais cette solution ne me satisfait pas beaucoup... Voilà pourquoi :

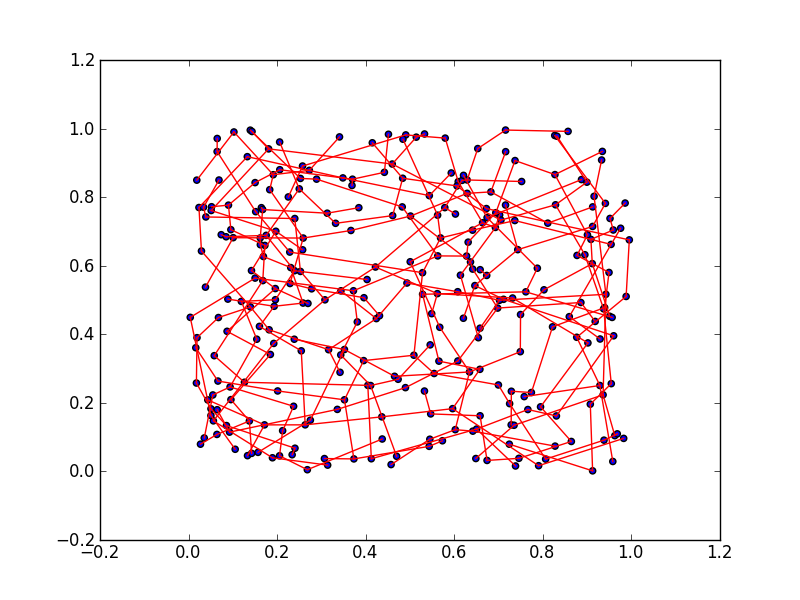
Pour pondérer les arêtes de mon graphes, je me suis contenté d'utiliser la distance entre les sommets mais cela me pose problème car je préférerais que les arêtes soient les plus longues possibles et pas l'inverse. Je me suis donc dit qu'en prenant comme pondération pour les arêtes l'inverse ou l'opposé de la distance, l'arbre couvrant minimum maximiserait les longueurs des arêtes. Evidemment, c'est bien ce que j'obtiens mais, comme j'aurais pu m'y attendre, cette méthode fait toujours ressortir le même motif dans lequel les points extrêmes (dans les coins) occupent une place prépondérante, comme l'illustre l'image que j'ai jointe :

max_spanning_tree.png

Je ne veux pas que des points portent autant d'arêtes relativement aux autres. En plus de ça, le motif formé privilégie également certaines directions (obliques) et je ne veux pas ça non plus. Dans l'idéal (mais j'ignore si cela a un sens), je voudrais que mon graphe soit couvert par un arbre dont les arêtes présentent des longueurs maximales, sans directions privilégiées et dont aucun sommet ne porte "trop" (concept bien flou pour des maths ) d'arêtes relativement aux autres. J'ajoute que je ne veux pas absolument la connexité ; je veux bien une forêt à la place d'un arbre du moment que ça vérifie "en gros" les propriétés que j'ai données.

En un mot, j'aimerais la non-cyclicité d'un arbre couvrant avec la bonne "homogénéité" et "isotropie" des arêtes d'un graphe complet.

Merci d'avoir lu jusqu'ici, j'attends vos suggestions... et vos questions parce que je pense que mes attentes ne sont pas franchement bien définies pour des maths

PS : Pour les gens intéressés, le code permettant de faire les figures ci-jointes provient de http://peekaboo-vision.blogspot.fr/2...g-tree-in.html (code Python)
-----

[gg0]

Bonjour.

C'est un peu flou, car le "maximal" (ou minimal) s'oppose à "bien réparti".
Tu peux éventuellement regarder si les "graphes aléatoires" ne feraient pas ton bonheur.

Cordialement.

[Anakinele]

Hello,

Je me réponds à moi même, en partie, j'ai eu une lueur :
je me suis dit qu'en déterminant l'arbre couvrant minimum pour des sous-ensembles de sommets choisis aléatoirement, je devrais m'approcher de ce que je cherche... et effectivement ce n'est pas trop moche :



J'ai donc une forêt, non plus un arbre, mais ça me convient mieux. Je suis juste "un tantinet" embêté par le côté aléatoire qui empêche la reproductibilité (à moins de mélanger les points a priori).
Ceci étant, si quelqu'un a une meilleure idée... ou une suggestion pour le choix optimal de la taille des sous-ensembles de sommets...

[Anakinele]

Oups, nos réponses se sont croisées !

Effectivement, le problème de la répartition doit être incompatible avec le min/max.
Ma "solution" fait finalement appel à de l'aléatoire mais uniquement dans le choix des sommets, pas des arêtes. Un arbre couvrant aléatoire répondrait-il plus à mes contraintes que "ma" forêt couvrante en partie aléatoire ?

[A voir en vidéo sur Futura]

[invite179e6258]

look at that : http://en.wikipedia.org/wiki/Minimum_spanning_tree

[Anakinele]

Merci pour ta suggestion toothpick-charlie but I have already looked at that (cf. 1st post) !
Suggères-tu un lien ou une sous-section particulière qui m'aurait échappé dans cette page Wikipedia ?

[NicoEnac]

Bonjour,

Si vous souhaitez diminuer l'influence des points extérieurs, pourquoi ne pas ajouter un coefficient à l'inverse des distances ? Un coefficient qui serait d'autant plus faible qu'on s'éloigne du centre de votre forêt de points ?

[zoonel]

. Dans l'idéal (mais j'ignore si cela a un sens), je voudrais que mon graphe soit couvert par un arbre dont les arêtes présentent des longueurs maximales, sans directions privilégiées et dont aucun sommet ne porte "trop" (concept bien flou pour des maths ) d'arêtes relativement aux autres.

Évidemment le problème est que les longueurs maximales sont les diagonales ensuite les verticales et horizontales sur la longueur/hauteur des noeuds...
sinon je propose ceci pour créer l'arbre couvrant minimum:
se définir une distance minimum qu'on aimerait bien avoir entre les noeuds, appelons-la MIN. Remplacer les distances (x) comme suit, si x>=MIN alors x=0, sinon x=1(ou 2,3,4,5).
Une autre approche serait de se limiter à un certain voisinage, on ne veut pas qu'un noeud soit connecté à un autre par une distance plus grande qu'une distance MAX définie. On pondère alors comme suit: si x>=MAX alors x=infini sinon x=0.
On peut aussi combiner les deux à savoir si si x>=MAX alors x=infini, si MIN<=x<MAX alors x=0, sinon x=1 (ou2,3,4,5...).
Je n'ai pas testé donc je ne sais pas ce que ça donne en pratique.L' idée est que si on remplace toutes les distances par une même distance on ne privilégie aucun noeud au sein d'un même groupe.

Je me demande également à quoi ressemblerait l'arbre couvrant si on pondère les distance de manière aléatoire, c-à-d on remplace x par random().
À noter que même avec de l'aléatoire on peut reproduire les résultats, il suffit de reprendre le même générateur pseudo-aléatoire et de lui attribuer la même graine (seed), d'ailleurs la graine pourrait être un paramètre pour obtenir des graphes plus à ta convenance.

[zoonel]

bon j'ai oublié de préciser une chose et comme je peux pas éditer mon message:

ps: l'algorithme utilisé joue un rôle, si par exemple il y a le choix entre plusieurs noeuds possible comme candidats, l'ordre de test va privilégier certains noeuds. Par exemple si on teste les noeuds de haut en bas et de gauche à droite, les noeuds du haut sont privilégiés même si ils ont le même poids. Une solution serait au départ de l'algorithme de mélanger l'ordre de test des noeuds (avec l'algo shuffle de fisher-yates par exemple).

[Anakinele]

Merci zoonel pour la suggestion. J'ai fait quelques tests dans cette direction mais rien ne m'a convaincu pour le moment. L'idée de fixer un seuil sur les distances paraissait bonne mais à l'usage, il y a toujours certains points qui sont privilégiés, et plus nécessairement sur les bords. Je pense que ce phénomène est lié à l'algorithme mais (pour le moment en tout cas) je n'ai pas tellement le temps d'en tester d'autres. En plus de ça, je commence à avoir un peu trop de paramètres différents à fixer plus ou moins arbitrairement (distance min/max, point de départ de la construction de l'arbre, même si le choix est aléatoire...).

Pour le moment, à moins que quelqu'un ait une idée nouvelle, je me contenterai de ce que j'ai expliqué plus haut avec une forêt d'arbres couvrants des sous-ensemble de sommets choisis aléatoirement (et pour retrouver la connexité et donc un seul arbre si nécessaire, il suffit juste de connecter les extrémités de chaque arbre avec le suivant). Au passage, @ zoonel, pour l'idée d'utiliser une graine dans le mélange des données afin de retrouver la reproductibilité, c'est ce que je voulais dire plus haut, je n'ai pas dû être très clair. Je passe déjà en paramètre de seed() un hash de mon jeu de données (positions des points).

Eventuellement j'essaierai encore les arbres couvrants aléatoires mais j'ai l'impression qu'un arbre reconstruit à partir d'une forêt (cf. la "solution" que j'évoque plus haut) vérifiera plus souvent les propriétés que je cherche à avoir.

Merci quand même à tous pour vos idées en tout cas !

[Anakinele]

EDIT (ou épilogue, au choix ) de mon post précédent :

J'ai testé avec un arbre couvrant aléatoire en utilisant simplement l'idée de zoonel, à savoir pondérer aléatoirement les arêtes. Finalement, je retrouve un résultat très proche de "ma forêt". J'ai peut-être parlé un peu vite, il semble bien que la répartition des arêtes d'un arbre couvrant minimum pour des distances aléatoires (un arbre couvrant aléatoire donc) vérifie grosso modo les propriétés que je cherchais. Et, pour être exact, ça rejoint au passage la première idée de gg0 ...que j'aurais essayée plus tôt si j'avais pensé à utiliser l'algorithme d'arbre couvrant minimum que j'avais déjà, avec des distances aléatoires !

Bon, merci à tous, je me débrouillerai bien avec tout ça !

[invite0e41fd9b]

On rappelle qu'un mot w est dit sans bord si son seul bord est le mot vide , c'est-à-dire si période(w) = |w|.

on suppose qu'un mot x a un bord de longueur minimale, non vide, u.
Montrer que u est sans bord et qu'il existe un mot v tel que x=uvu

[gg0]

Heu ... quel rapport avec les arbres couvrant maximaux ?

[inviteea028771]

Heu ... quel rapport avec les arbres couvrant maximaux ?

Aucun, c'est la tactique de la pèche au casier... On balance des casiers (les questions) à la mer (les forums divers et variés), puis on vient les relever plus tard. Avec un peu de chance, un crabe (forumeur) sympathique mais un peu naïf se serra fait prendre au piège (en donnant la solution)