proba modif

[kaderben]

Bonjour
Voici un exo de terminale S

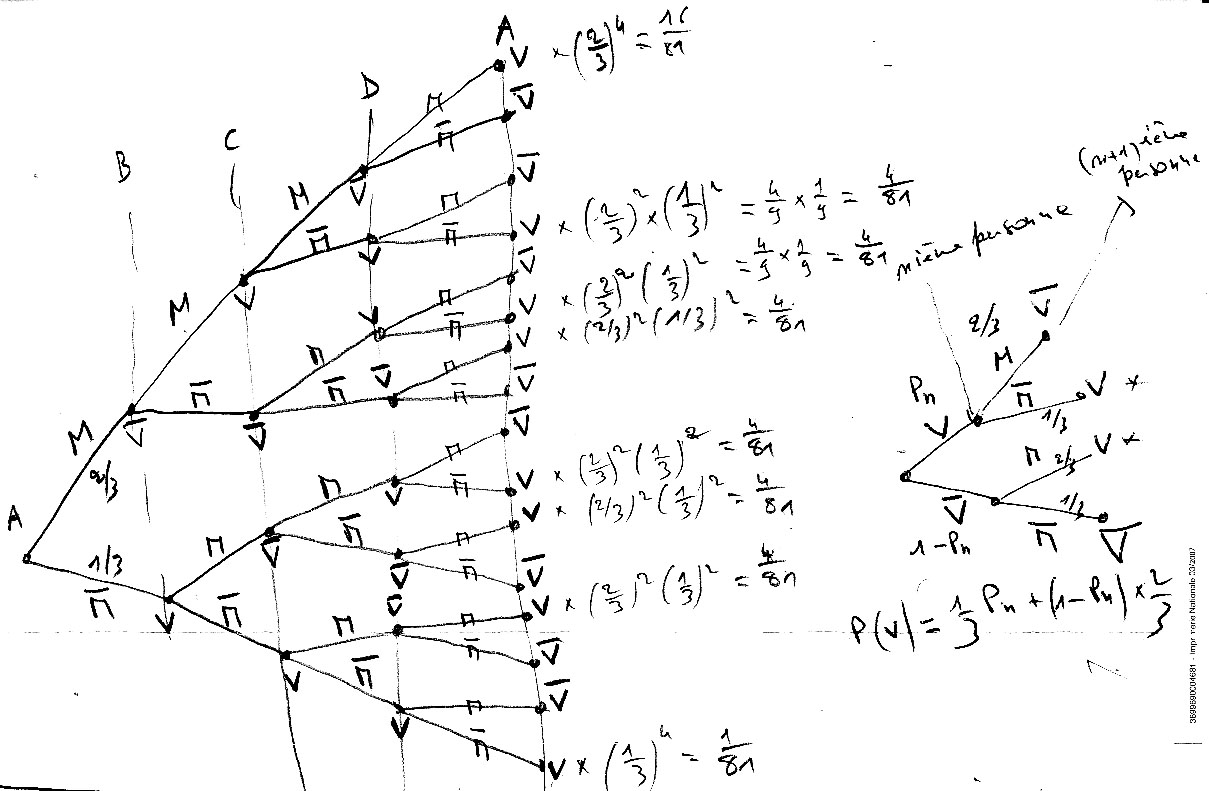
Quatre personnes A,B,C,D se transmettent dans cet ordre A,B,C,D,A une histoire. Chacun dit la vérité avec une proba de 1/3
D dit la vérité. Quelle est la probabilité que A ait dit la vérité ?

On cherche P(A) sachant D (ancienne notaion: P(A/D) )

A raconte à B, B raconte à C, C raconte à D et D raconte à A
Je ne vois pas s'il s'agit de A en premier ou de A en dernier ?
Est ce que A la raconte encore à B une deuxième fois et ainsi de suite ?
Merci pour vos commentaires
-----

[invite179e6258]

j'écrirais P(A sachant D) plutôt que P(A) sachant D

tu es sûr de ton énoncé?

ce que je comprendrais, c'est : il y a 2 messages 0 ou 1. Chacun transmet le message qu'il a reçu avec une probabilité 1/3 et l'autre message avec la probabilité 2/3. D transmet 1. Quelle est la probabilité que A ait transmis 1 au premier pas?

[kaderben]

Bonjour
ta syntaxe est la bonne: P(A sachant D)
Voici l'énoncé ci joint

Il s'agit de l'exo N° 78

[gg0]

Bonjour.

Il y a deux façons de comprendre :
* si on a eu une histoire fausse, on ne peut pas inventer la bonne, donc l'histoire est perdue. Ce n'est que de la logique élémentaire : Pour que l'histoire soit la bonne à la fin, il a fallu qu'elle se transmette, donc que A ait dit la vérité. la proba est 1.
* Interprétation très limite de l'énoncé : Celle de Toothpick-charlie : Il n'y a que deux histoires, et celui qui reçoit une histoire la transmet avec probabilité 1/3 et raconte l'autre avec probabilité 1/3. Dans ce cas là tu dois pouvoir faire un arbre et en déduire la proba cherchée (13/41 si je n'ai pas fait trop vite).

Mais que cet énoncé est mal conçu !!!

Cordialement.

[A voir en vidéo sur Futura]

[kaderben]

Justement, comme tu dis:" Mais que cet énoncé est mal conçu !!! "
J'avoue que je ne sais pas comment se déroule cette expérience. Par exemple on réunit 4 personnes A,B,C,et D et on raconte l'histoire uniqument à A ou bien aux quatres ?
Je pense que chacun doit connaître les deux parties et il transmet celle qu'l veut. Est ce que ça a un sens ?

Je m'explique: Toothpick-charlie a proposé les deux parties 0 et 1
S'il y a uniquement A qui est courant des deux parties, par exemple il transmet 1 à B, soit B transmet 1 s'il ne ment pas, mais s'il veut mentir il ne peut pas transmettre 0 parce qu'il n'est pas au courant de son existense .
Il doit y avoir un protocole je pense
Merci pour tes remarques , mais le 13/41 je ne vois pas. vraiment je sèche.

[gg0]

J'ai simplement fait un arbre avec à chaque fois 2 branches V ou F, et les probas associées. Les feuilles provenant de A dit V donnent une proba de 17/81 que D dise V, celle venant de A dit K donnent une proba de 28/81 que D dise V.

Cordialement.

Nb : Je n'avais jamais utilisé un arbre pour des probas conditionnelles. On apprend à tout âge !

[kaderben]

Voici comment j'ai procédé pour retrouver ton résultat 13/41
On commence par A:
Si A dit vrai à B (B entend vrai de la part de A), si B ne ment pas , il dira vrai à C, si B ment il dira faux à C
A dit faux à B (B entend faux de la part de A), si B ne ment pas , il dira faux à C, si B ment il dira vrai à C

M : la personne ment, Mbarre : la personne ne ment pas : V : histoire vraie, Vbarre : histoire fausse
V: histoire vraie, Vbarre: histoire fausse

P(Dv) = 41/81
P( A/D) = P( A inter D) /P(D) = P(D/A)*P(A)/P(D)=13/41
Calcul intermédiaire: P(D/A) = 13/27

[kaderben]

Bonjour

Pour l'exo 79
n le nombre de billets gagnants
aucun billet gagnant C,998,n)/C,1000,n) = (-n²+1999n)/999000
au moins un billet gagnant; P=1 - (-n²+1999n)/999000
P>0,7 équivaut n² - 1999n 699300 > 0
n >0 ,l'ensemble des solutions de cette inéquation est ]0;452] U [1547; infini[
Que faut il choisir, n=452 ou n=1547 ? Sachant que les deux nombres vérifient P > 0,7
Merci

[gg0]

"Une loterie contient 1000 billets"
Si tu ne t'es pas trompé, il faudrait moins de 452 ? donc on peut n'en acheter qu'un et avoir plus de 70% de chances de gagner ?

Il faut être raisonnable ...

Cordialement.

[invited3a27037]

bonjour

c'est pas très clair

Par exemple si A et B mentent, alors l'histoire transmise à C est elle vraie ou fausse ?

[gg0]

Joêl,

l'arbre de Kaderben est celui de l'interprétation dans laquelle il n'y a que deux histoires possibles, la "vraie" et la "fausse", et qu'un menteur transmet celle des deux qui ne lui a pas été dite.

Cordialement.

NB : N'importe comment, cet exercice est malsain, l'énoncé n'a pas de sens clair.

[kaderben]

Bonjour

Pour l'exo 78, j'ai suivi ce que tu as proposé (deux parties 0 ou 1 de l'histoire ) et l'arbre que j'ai fait confirme le calcul de ggo c'est à dire P( D/A) = 13/41

Tu écris:"Par exemple si A et B mentent, alors l'histoire transmise à C est elle vraie ou fausse ? "

J'ai supposé que les quatre connaissent les deux parties de l'histoire, sans savoir la partie vraie et la partie fausse, et ils doivent transmettre chacun qu'une partie
Soit 0: faux et 1: vraie
Si A ment, c'est à dire il dit 0 à B, et B ment, donc B dit 1 a C
C reçoit l'histoire vraie

Si je ne pars pas de cette hypothèse, on retombe sur la remarque de ggo: "cet exercice est malsain, l'énoncé n'a pas de sens clair. "

Pour l'exo 79, tu as raison, je n'ai pas fait attention qu'il y a que 1000 billets.
Je pense que mes calculs sont justes, car je les ai vérifiés. Donc on doit acheter 452 billets. Est ça ?

[gg0]

Ou moins !

Ton résultat n'est pas cohérent : On s'attend à ce que la probabilité de gagner augmente avec le nombre de billets pris, donc l'intervalle ]0;452[ ne peut pas être la bonne réponse.
Revois tes calculs, tu des erreurs : "n² - 1999n 699300 > 0" est faux.

[kaderben]

Il y a un "+" qui manque, ll faut lire :"n² - 1999n + 699300 > 0

[gg0]

Même ainsi ...

Reprends tes calculs, et écris-les ici, ce n'est ni le bon trinôme, ni la bonne inégalité.

[kaderben]

Tu as raison d'insister !
aucun billet gagnant (C,998,n)/(C,1000,n) = (n²-1999n+999000)/999000
au moins un billet gagnant; P=1 - (n²-1999n+999000)/999000
P>0,7 équivaut n² - 1999n + 699300 < 0

l'ensemble des solutions de cette inéquation est ]452,05...;1546,94...[
n>0 il faut acheter au minimum 453 billets

Merci pour tout.