Interprétation géométrique des vecteurs covariants

[invite53be706a]

Bonjour,

Ma question est relative à l'interprétation géométrique des coordonnées covariantes d'un vecteur.

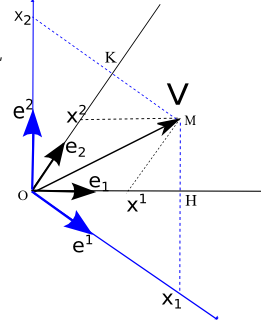
Je m'appuie sur le schéma suivant :

Sur ce schéma, les composantes covariantes du vecteur V sont en bleu alors que les composantes contravariantes sont en noir.

Le vecteur s'exprime sous deux formes selon la base utilisée

Or dans de nombreux textes sur la relativité générale (Barrau, Susskind et d'autres), il est dit que les composantes covariantes sont OH et OK en expliquant que c'est la projection orthogonale qui explique
la différence entre les deux vecteurs dans un changement de base.

Alors quelles sont les coordonnées covariantes : OH et OK ou les projections du vecteurs V sur la base duale ?

Merci pour vos réponses.

Capitoul
-----

[Amanuensis]

Bonsoir, et bienvenu sur le forum,

Un "vecteur" covariant est une représentation d'une 1-forme, d'un gradient. En tant que vecteur, on l'interprète comme le vecteur v tel que la forme s'écrive



Visuellement, v est le vecteur dans la direction principale du gradient, quand cela s'applique, et de module indiquant la "pente" dans la direction principale.

[invite53be706a]

Merci Amanuensis mais je reste encore avec mes interrogations en ce qui concerne l'interprétation géométrique.

Pourquoi dit-on que les composantes du vecteur covariant sont OH et OK alors que la forme analytique fait référence à la base duale ?

J'ajouterai un peu de confusion en disant qu'un même vecteur V peut s'exprimer avec des composantes covariantes ou contrariantes alors que le vecteur contravariant est tangent à une courbe et le covariant est analogue au gradient. Je me doute bien que mon raisonnement est faux mais j'aimerai bien savoir où est l'erreur. J'espère avoir été clair dans l'exposé de mon problème.

Capitoul

[Amanuensis]

Pourquoi dit-on que les composantes du vecteur covariant sont OH et OK alors que la forme analytique fait référence à la base duale ?

Géométriquement la base duale est composée de deux éléments qu'on peut associer avec les deux gradients réguliers, celui de pente unité qui "monte" dans la direction des x, et celui qui "monte" dans la direction des y. Si on prend une base non orthogonale, on réalise que pour obtenir un "gradient" régulier dans une direction en combinant les deux éléments de la base, cela ne se fait pas de la même manière que pour les vecteurs déplacement (les contravariants). OH et OK sont la manière géométrique de trouver les composantes dans la base duale (celle des gradients) du gradient représenté par un vecteur déplacement.

Analytiquement, si sont les composantes d'un vecteur contravariant, sont celles du covariant (de la forme linéaire) correspondant dans la base duale. OH et OK sont en rapport avec l'effet géométrique de . Quand la base est orthonormée, est la matrice identité (en euclidien) et son effet n'est pas visible. Mais si la base est normée non orthogonale, cet effet se visualise par une construction géométrique telle qu'indiquée par la figure.

[J'ai du mal avec la figure, simplement parce qu'il ne me paraît ni naturel, ni aidant, de représenter les éléments de la base duale comme des vecteurs déplacement. La difficulté est plus visible en prenant une base orthogonale non normée.]

J'ajouterai un peu de confusion en disant qu'un même vecteur V peut s'exprimer avec des composantes covariantes ou contrariantes alors que le vecteur contravariant est tangent à une courbe et le covariant est analogue au gradient.

Oui. C'est un abus de langage de parler d'un "même vecteur V". C'est un vecteur et son image par l'isomorphisme en E et E* que constitue la métrique ; on se permet de les confondre parce qu'il y a isomorphisme (et qu'il est trivial en composantes dans le cas d'une base orthonormée). On s'y retrouve bien mieux en considérant les deux objets comme géométriquement de nature différente, comme vous le faites dans la seconde partie de la phrase.

Je me doute bien que mon raisonnement est faux mais j'aimerai bien savoir où est l'erreur.

Quel raisonnement ? (Prendre x_1 et x_2 comme coordonnées covariantes plutôt que les modules de OH et OK ?)

[A voir en vidéo sur Futura]

[invite53be706a]

Merci encore pour cette réponse éclairante :

Mais je ne suis pas à l'aise avec quelques points, ce qui m'empêche d'élaborer une présentation linéaire des deux types de vecteurs. Après avoir introduit le vecteur classique (contravariant), j'introduis la métrique, puis la base duale, et logiquement le vecteur covariant et ses composantes perpendiculaires à la base de l'espace E de départ. Là, un chainon me manque qui me permettrait de démontrer que les composantes covariantes (et leur orthogonalité) entrainent la notion de vecteur-densité par opposition au vecteur contravariant qui est un vecteur-longueur (ou déplacement). La suite est plus facile, je donne le gradient comme un exemple de vecteur-densité et ensuite je montre que le changement de coordonnées des deux vecteurs est inversé, puis j'introduis les tenseurs.
(c'est un cours que je fais pour moi, je ne suis pas prof, je mets en ordre certaines connaissances pour expliquer le chemin tortueux suivi par Einstein pour trouver les équations de champ)

Oui. C'est un abus de langage de parler d'un "même vecteur V". C'est un vecteur et son image par l'isomorphisme en E et E* que constitue la métrique ; on se permet de les confondre parce qu'il y a isomorphisme (et qu'il est trivial en composantes dans le cas d'une base orthonormée).

La réponse est très claire. Merci encore. Nous sommes bien d'accord que dans ce cas E et E* sont confondus ?

Capitoul

[Amanuensis]

Nous sommes bien d'accord que dans ce cas E et E* sont confondus ?

D'un point de vue strict, ils ne devraient jamais être confondus. Déjà, l'isomorphisme n'est pas unique : il n'y a pas qu'une métrique ou pseudo-métrique d'un point de vue mathématique. On ne peut donc se permettre de les confondre que si la métrique ou pseudo-métrique est précisée explicitement ou implicitement. (Il y a des cas sans métrique, comme par exemple les variétés qui apparaissent en thermodynamique.)

Disons que l'identification entre les deux est très commune. Elle est quasiment systématique en mécanique classique (espace euclidien). Et elle est courante en mécanique relativiste. Dans ce dernier cas, les notations avec indice les distinguent quand même, et on parle de "descendre" ou "monter" les indices pour l'application de l'isomorphisme et son inverse.

Ceci dit, la confusion entre les deux n'apporte pas grand chose une fois qu'on a compris la différence ! Avec une vision purement géométrique, en termes d'objets géométriques et non en termes de composantes, il n'y a aucune raison de les confondre : un déplacement ou une fonction linéaire des déplacements sont des "choses" très différentes. En termes de composantes c'est dangereux dans les cas autres que euclidiens ; en RG il est même important d'expliciter la métrique, ou au grand minimum de distinguer par la position de l'indice.

---

Pour les autres points du message, je pense que cela se clarifiera de soi-même, avec les conséquences de l'idée que la (pseudo-)métrique est un isomorphisme entre E et E*, ce qui relie les notions d'orthogonalité, de produit scalaire et covariance/contravariance.

Au passage il est peut-être utile de rappeler que le produit scalaire u.v peut être vu comme l'application au vecteur v de la forme image de u par l'isomorphisme (ou réciproquement)