Bonjour.
j'ai un petit problème
J'ai repris mon cours de sur les fonctions de référence en maths sup. Le prof prend la fonction f(x)= exp(ix). Il dérive et écrit :
f'(x)= i exp(ix)
et donc sin'(x)= sin(x+ pi/2)= cos(x) et cos'(x)= cos(x+pi/2)=-sin(x).
Et il écrit ensuite que dériver les fonctions x → sin(x), x → cos(x) ou x → exp(ix) revient à effectuer un quart de tour direct et inversement
fournir une primitive de chacune de ces fonctions revient à effectuer un quart de tour indirect.
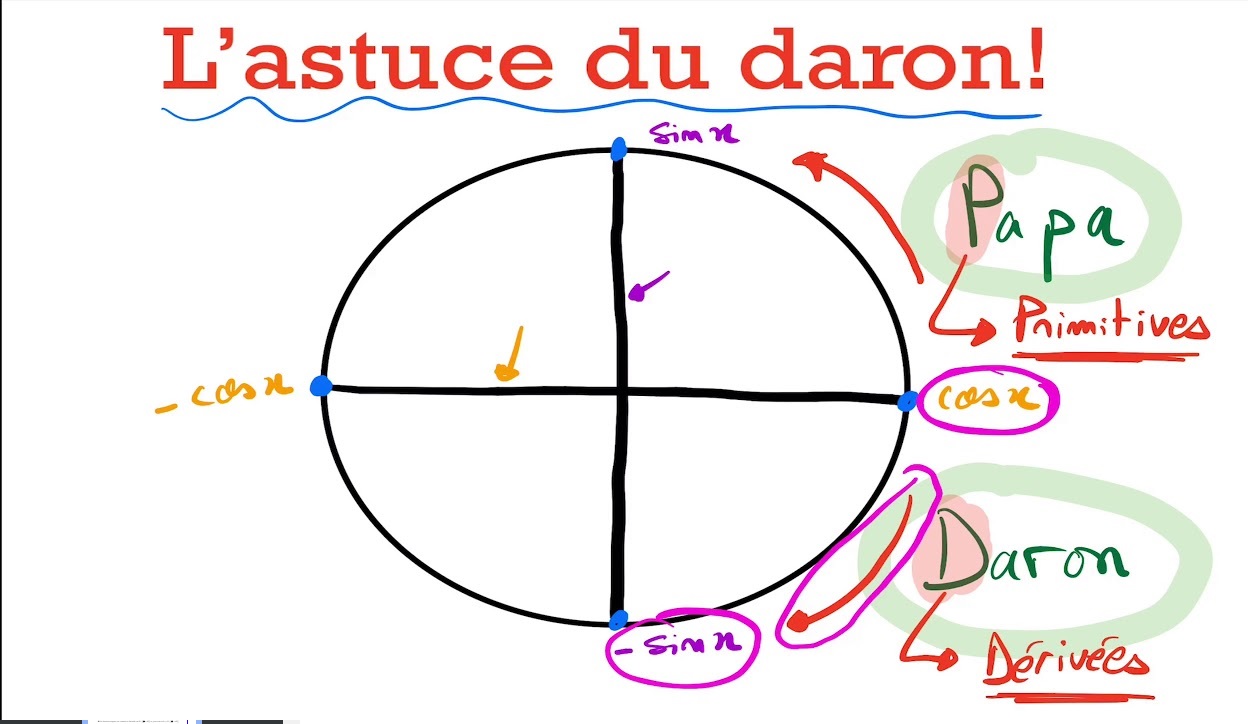
Là je suis d'accord mais le professeur de ma soeur qui est en terminale lui marque le contraire dans son cours comme moyen mnémotechnique pour retrouver les formules pour dériver ou intégrer des fonctions trigo :
Voici une image de son cours :
Je ne vois pas où est l'erreur et qui se trompe sur le sens du tour à effectuer pour dériver.
Merci pour votre aide.
Daniel
-----