Regression bizarre

[curieuxdenature]

Bonjour à tous
(j'ai un doute sur le bon forum, informatique ou Maths, mes excuses si je me plante)
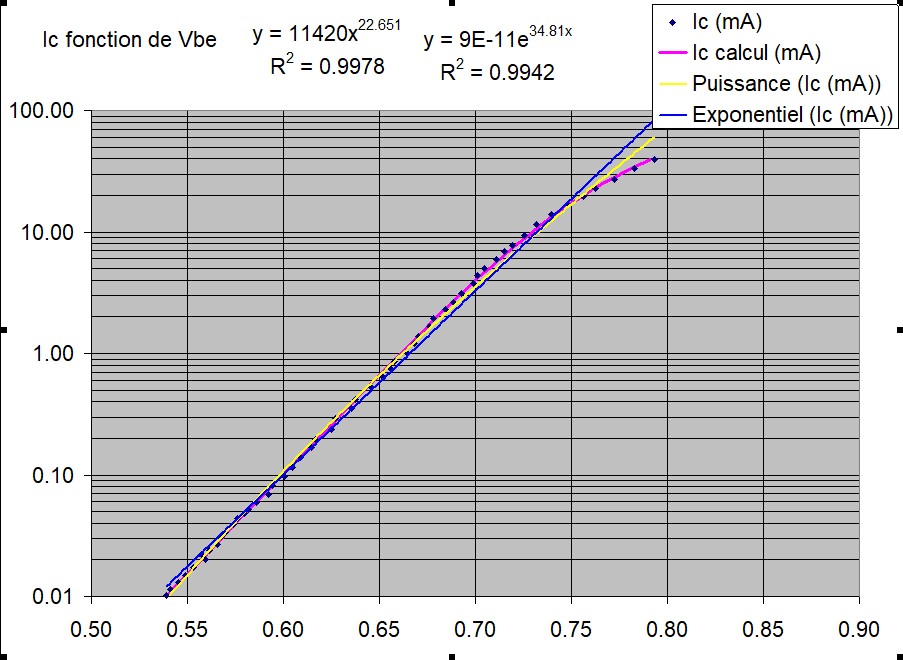
Comment calculer le développement d'une régression de la fonction de type y=a + b*ln(x) + c*x^d
à partir d'une série de mesures statistiques ?
Je connais les 4 méthodes de calculs des régressions que l'on trouve sous Excel: logarithmique, polynomiale, puissance et exponentielle.
La fonction ne ressemble à aucune si ce n'est un mélange de régression log + puissance.


Pour être plus précis, je recherche un développement de ce genre:
For I = 0 To n - 1
Sx = Sx + Log(infos(I).x)
Sy = Sy + infos(I).y
Sx2 = Sx2 + Log(infos(I).x) ^ 2
Sy2 = Sy2 + infos(I).y ^ 2
Sxy = Sxy + Log(infos(I).x) * infos(I).y
Next


avec les x, y placés dans le tableau infos(I).x et y
n étant le nombre de couples de datas


suivi de:
' calcul des constantes: k1, de la pente k2 et de R²
NUMER = (n * Sxy - Sx * Sy)
DENOM = (n * Sx2 - Sx ^ 2)
k2 = NUMER / DENOM ' k2 pente
R2 = NUMER * NUMER / (DENOM * (n * Sy2 - Sy ^ 2)) ' Coefficient de Corrélation au carré
k1 = (Sy - k2 * Sx) / n ' k1 valeur de y avec x.ordonnée origine infos(0)


ce qui me donnerait:
régression logarithmique ln(x),y --> y=k1 * Ln(k2 * x) ce qui revient à
y = a * Ln(b * x)


Donc je recherche le même topo pour arriver à
y=a + b * Ln(x) + c * x^d


Merci d'avance.
-----

[gts2]

Bonjour,

d fait partie des paramètres à déterminer ?
Si oui, c'est du non linéaire et, sauf astuce que je ne vois pas, non linéarisable.
Donc pas faisable avec la méthode proposée.
Excel est obligatoire ?

[gg0]

Bonjour.

Y a-t-il une bonne raison à prendre un modèle aussi compliqué ? Car il est globalement inefficace, surtout si on ne connaît même pas d. À priori, il va y avoir de nombreuses valeurs possibles des 4 paramètres, sans bonne raison d'en choisir une. Car la régression logarithmique est utile pour des quantités qui varient de moins en moins vite, contrairement à la régression de puissance, adaptée à des variations de plusieurs ordres de grandeur et de plus en plus rapides.

Cordialement.

[curieuxdenature]

merci de ta réponse, il y a bien 4 paramètres.
Quand je regarde la courbe de tendance de l'exemple, je me demande comment elle a été trouvée. ça ne me parait pas faisable par approches au pif.


la courbe en mauve est tracée selon cette fonction, et ça colle vraiment au plus proche des mesures alors que les tendances "puissance" ou "exponentielle" ne conviennent pas vraiment.
Dans ce fichier j'ai ça comme valeurs pour cette fonction:

0.843255726

0.026454783

0.93714626

1.034593826

ce qui donne des estimations vraiment plus corrélées que ce que j'ai avec Excel, chapeau au gars qui a trouvé ce moyen...

[A voir en vidéo sur Futura]

[curieuxdenature]

cette approche doit surement être automatisée, je vois mal barré celui qui voudrait extraire ce genre fonction pour l'appliquer à des dizaines de transistors en vue d'une simulation sans cela.
D'autant plus que comme tu dis, les constantes n'ont ni queue ni tête, perso je ne vois rien de connu qui en ferait qque chose d'homogène.
Je continue de chercher, si je trouve je vous tiens au courant, sait-on jamais...
Merci bien.

[gts2]

Si 1,03459 c'est d, prendre d=1 parait raisonnable et dans ce cas "y=a + b * Ln(x) + c * x" est bien linéaire par rapport aux paramètres et on peut utiliser votre méthode à faire évoluer à cause des trois paramètres au lieu de 2.

[gts2]

cette approche doit surement être automatisée, je vois mal barré celui qui voudrait extraire ce genre fonction pour l'appliquer à des dizaines de transistors en vue d'une simulation sans cela.

Sans excel, en programmant sous Python ou en utilisant n'importe quel "tableur scientifique", cela se fait sans problème.

[curieuxdenature]

merci gts2s, je regarde ça en modifiant le fichier, mais bon, avec autant de décimales je soupçonne une méthode bien rodée...

[curieuxdenature]

"Tableur scientifique", ouh là, je crois que je vais faire des découvertes...
Je ne connaissais pas ces freewares.

[gts2]

J'ai été regardé un modèle du courant collecteur, on trouve une loi exponentielle mais avec deux zones (passage de à ) ce qui serait cohérent avec votre courbe : une première exponentielle jusqu'à 0,7 V en gros puis une deuxième, donc deux modèles linéaires en ln(Ic)=a + b * Vbe, ce qui quand même plus simple. A voir.

[gts2]

avec autant de décimales je soupçonne une méthode bien rodée...

A mon humble avis, dans les décimales seules les deux premières ont un sens...

[erff]

Bonjour,

Je me permets une réponse d'électricien :
Je pense que pour que le modèle ait un intérêt il faudrait inclure d'autres paramètres tels que Vce (effet Early) et surtout la température : les coefficients que tu vas trouver ne seront bons que pour une température donnée et une tension collecteur-émetteur donnée ce qui réduit considérablement l'applicabilité du modèle.
Pour information, SPICE utilise (utilisait ?) le modèle de Gumel-Poon qui fonctionne plutôt bien à ma connaissance. Tu pourrais t'inspirer ce ces équations afin de partir d'une équation à paramètres ayant plus de sens physique.
https://web.archive.org/web/20090201...nd/node48.html

Par contre, il faudra plus qu'une mesure de Ic(Vbe) pour trouver les paramètres.

Bon courage

[gts2]

Le modèle à deux exponentielles ne marche pas si mal que çà :

IcVbe.pdf

[curieuxdenature]

Bonjour,

Je me permets une réponse d'électricien :
Je pense que pour que le modèle ait un intérêt il faudrait inclure d'autres paramètres tels que Vce (effet Early) et surtout la température : les coefficients que tu vas trouver ne seront bons que pour une température donnée et une tension collecteur-émetteur donnée ce qui réduit considérablement l'applicabilité du modèle.
Pour information, SPICE utilise (utilisait ?) le modèle de Gumel-Poon qui fonctionne plutôt bien à ma connaissance.
Bon courage

Bonjour erff

c'est bien le but du fichier excel, extraire les paramètres SPICE, et le blème c'est qu'aucune équation ne parviens à coller d'aussi près que celle là avec une cinquantaine de mesure réelles.
Il y a plusieurs théories, celle qui s'en rapproche le plus est:
Vbe = Vt * NF * Ln(Ic/Is) + Rbe * Ic
ça ressemble pas mal à celle de mon document:
Vbe = 0.8432 + Vt(+ un schouilla) * Ln(Ic) + 0.84*Ic
le résultat est proche mais loin d'être satisfaisant, et malheureusement le nombre de décimales réduit n'arrange rien au problème.

La seule valeur qui me parle c'est le 0.026454783 très proche de Vt, bien connu en physique des jonctions PN (=kT/q = cte de Boltzman * T en kelvin / charge de l'electron = 0.0258649 Volt)
Le dernier parametre pourrait coller avec Rbe la resistance base-emetteur de ce transistor (un BF420).

Mais bon, le but c'est de sortir une équation comme celle de l'auteur du fichier, j'ai pensé à mon forum préféré sans chercher à contacter le gars...

[gts2]

Vbe = Vt * NF * Ln(Ic/Is) + Rbe * Ic
ça ressemble pas mal à celle de mon document

Tout à fait, la seule différence est le d=1, ce qui parait raisonnable et en plus on peut interpréter les paramètres.

La seule valeur qui me parle c'est le 0.026454783 très proche de Vt, bien connu en physique des jonctions PN (=kT/q = 0.0258649 Volt)

On peut considérer que c'est Vt : si on se place dans le cas idéal, cela donne une température de 33°C pour la jonction ce qui parait raisonnable. Remarque : dans vos Vt, les trois derniers chiffres sont superfétatoires.

le résultat est proche mais loin d'être satisfaisant

En quoi n'est-ce pas satisfaisant ? : icvbe2.pdf

[erff]

Bonsoir,

Bonjour erff
Vbe = Vt * NF * Ln(Ic/Is) + Rbe * Ic
ça ressemble pas mal à celle de mon document:
Vbe = 0.8432 + Vt(+ un schouilla) * Ln(Ic) + 0.84*Ic

Oui tout à fait on est proche du modèle du Gummel-Poon. Le terme Is est très dépendant de la température, et cet effet est bien plus visible que le "kT/q" (environ *r tous les 10K d'augmentation avec r admis proche de 2, même si cette valeur dépend énormément du composant considéré). Et on peut raffiner en incluant une résistance en parallèle de Vce pour modéliser l'impact de Vce sur le courant Ic (effet Early) de façon simple.

Si ça peut aider à valider tes résultats de mesure et de fitting, le modèle BF420S est présent dans la librairie standard de LTSpice (il semble assez similaire au BF420 mais je n'ai pas regardé en détail) :

 .MODEL BF420S NPN(IS=6.46E-16 ISE=2.80E-17 ISC=2.89E-14 XTI=3.00 BF=1.23E2 BR=5.61 IKF=4.09E-2 IKR=1.00 XTB=1.5 VAF=4.15E2 VAR=4.30E2 VJE=3.00E-1 VJC=3.00E-1 RE=4.41E-1 RC=4.08E-1 RB=4.64E1 RBM=2.17E1 IRB=2.42E-2 CJE=4.19E-11 CJC=5.49p .00 FC=5.00E-1 NF=9.11E-1 NR=1.86 NE=1.00 NC=1.03 MJE=3.90E-1 MJC=5.21E-1 TF=1.13n TR=0 ITF=2.65 VTF=8.76E5 XTF=6.01E2 EG=1.11 VCEO=300 ICRATING=50m MFG=SIEMENS)

Voir ici pour la signification des paramètres :
https://ltwiki.org/LTspiceHelp/LTspi...transistor.htm

Bonne soirée

[curieuxdenature]

En quoi n'est-ce pas satisfaisant ? : Pièce jointe 498987

Bonjour gts2
je parlais de cette équation Vbe = 0.8432 + Vt(+ un schouilla) * Ln(Ic) + 0.84*Ic
Celle que tu présentes est la finale, et évidemment elle ne dit pas comment on parvient à déterminer Is, Ut et Rbe.
Dans le modèle de Gummel-poon il y a 43 paramètres si je ne m'abuse, par contre avec l'équation de mon document excel ce qui m'interroge c'est le moyen utilisé pour parvenir à ce qui ressemble à une courbe de tendance.
Si tu préfères, je cherche l'outil mathématique qui sert à extraire les 4 fameuses constantes (à partir d'une simple courbe expérimentale donnée par le fabricant du transistor, par ex.), quitte à ne rien savoir de leurs significations physiques. C'est pour ça que j'ai choisi "Mathématiques-superieur" et pas "electronique".
Bref, je continue de chercher, il y a du monde mais avec un peu de chance...

[curieuxdenature]

Bonsoir, Voir ici pour la signification des paramètres :
https://ltwiki.org/LTspiceHelp/LTspi...transistor.htm

Bonne soirée

Bonjour erff

J'utilise LTspice depuis la version III, depuis des années donc, il est vraiment excellent pour simuler des montages électroniques de toutes sortes, grâce à ces types de modèles bien sûr.
Je pourrais me contenter d'utiliser betement le programme mais je suis trop curieux, j'aime bien aller plus loin que la surface.
Merci de votre aide en tous cas, c'est sympa.

[gts2]

Je parlais de cette équation Vbe = 0.8432 + Vt(+ un schouilla) * Ln(Ic) + 0.84*Ic
Celle que tu présentes est la finale, et évidemment elle ne dit pas comment on parvient à déterminer Is, Ut et Rbe.

Je ne comprends pas trop :
D'après l'équation numérique : Rbe=0,84 ; Vt=0.026454783 et Vt*Ln(Is)=-0,8432
Et comme c'est linéaire (vis-à-vis des paramètres), même Excel peut s'en sortir : il connait la régression linéaire multiple : Regression_Excel
Et "à la main", c'est la même chose que pour y=ax+b, on minimise somme (y-(a+bx+cx²)², les dérivées nulles /a,b,c donnent un système linéaire qu'Excel peut résoudre.

Dans le modèle de Gummel-poon il y a 43 paramètres si je ne m'abuse, par contre avec l'équation de mon document excel ce qui m'interroge c'est le moyen utilisé pour parvenir à ce qui ressemble à une courbe de tendance.
Si tu préfères, je cherche l'outil mathématique qui sert à extraire les 4 fameuses constantes (à partir d'une simple courbe expérimentale donnée par le fabricant du transistor, par ex.), quitte à ne rien savoir de leurs significations physiques. C'est pour ça que j'ai choisi "Mathématiques-superieur" et pas "electronique".

Si on n'en cherche que 3 (d parait de peu d'intérêt), voir ci-dessus.
Si on en cherche 4 (avec d donc non linéaire), avec Python et scipy.optimize on y arrive sans problème. scipy.optimize.curve_fit

[curieuxdenature]

@ gts2, Je vais insérer le fichier XLS tu verras mieux mon but.

[curieuxdenature]

sur la feuille Vbe, en cellules E58 à E61 on a les 4 paramètres d'origine du fichier.
C'est en C58 à C61 que l'équation apparait : y = a + b * Ln(Ic) + c * Ic^d ; (ici ^n)
cette équation vient de nulle part et c'est celle-là que je désirerais comprendre d'où elle sort.
Elle sert dans la colonne C1 à C55 en tant que Vbe estimés.
Voilà voilà

[curieuxdenature]

Si on en cherche 4 (avec d donc non linéaire), avec Python et scipy.optimize on y arrive sans problème. scipy.optimize.curve_fit

merci pour l'info, je vais ressortir un pyton et voir comment exploiter cette bibliothèque. (ça va ^être chaud je ne me sert que de Visual basic)

cette page m'intéresse:
https://docs.scipy.org/doc/scipy/ref...olate.interp1d

[gts2]

Je ne trouve en effet pas trace de l'origine des valeurs de a b c n dans le fichier (mais je ne suis pas spécialiste d'Excel).
a b c peuvent s'obtenir (et s'obtiennent ?) par une régression linéaire multiple

Sinon le passage de 3 à 4 paramètres n'améliore pas beaucoup les choses (on passe d'un écart données/modèle de 1,47 mV à 1,21 mV), donc je ne suis pas sûr que ce n soit pertinent.

Si on regarde les écarts graphiquement, c'est la même chose : forum1b.pdf

D'autre part une régression non linéaire (tableur scientifique) ne me donne pas votre valeur de n : je trouve n=1,37 : forum1a.pdf
On ne voit quasiment pas de différence entre les deux courbes.

confirmé par Python :

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import pandas as pd

nom_fichier = 'forum1.csv'
# le fichier contient les colonnes Ic et Vbe_25
data = pd.read_csv(nom_fichier, sep = ',')
# permet de placer les données du fichier .csv dont les séparateurs sont des virgules dans une variable de type dataframe

#Extraction des colonnes du tableau
x = data['Ic'] # Extraction de la colonne dont le nom dans le tableau est Ic
y = data['Vbe'] # Extraction de la colonne dont le nom dans le tableau est Vbe

def funcLin(x, a, b, c):
return a + b * np.log(x/1000) + c*x/1000

def funcNonLin(x, a, b, c,n):
return a + b * np.log(x/1000) + c*(x/1000)**n

plt.plot(x, y, 'b-', label='données')

popt, pcov = curve_fit(funcLin, x, y)

plt.plot(x, funcLin(x, *popt), 'r-',
label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))

popt2, pcov2 = curve_fit(funcNonLin, x, y)

plt.plot(x, funcNonLin(x, *popt2), 'g--',
label='fit: a=%5.3f, b=%5.3f, c=%5.3f, d=%5.3f' % tuple(popt2))

plt.xlabel('Ic')
plt.ylabel('Vbe')
plt.legend()
plt.show()

[gts2]

cette page m'intéresse: ...

Attention à l'encadré au début :
This class is considered legacy and will no longer receive updates.
This could also mean it will be removed in future SciPy versions.
For a guide to the intended replacements for interp1d see 1-D interpolation.

[curieuxdenature]

du coup je viens de tout charger, Python v3.11.00
et j'ai cette erreur

seule modif : point-virgule dans le csv, ma version d'excel ne permet pas la virgule.
Je ne connais pas python, là je sèche...

[curieuxdenature]

j'ai tout chargé avec
py -m pip install numpy ete les autres (matplotlib, scipy, pandas)

[curieuxdenature]

résolu, tabulation avant return et 1ere ligne = Ic,Vbe(25)

merci gts2

[Biname]

Salut,
Le code qui a été supprimé avait été obtenu sur mistral.ai (ia française) en posant la question suivante :
"Python : est il possible de créer une régression sur base d'un fonction contenant des paramètres variables (ex : y = ax + b mais plus complexe) et de données"
Ce code obtenu en une minute était quasi le même que celui de gts2.

Il est aussi possible de demander une version VB.

C'etait il y a trois jours.

[curieuxdenature]

Encore merci gts2, j'ai mis en application sur les datas hFE fonction de Ic du fichier.
Un petit "warning" à comprendre et ce sera cool.

import sys
import os
import math
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import pandas as pd


nom_fichier = 'Modelisation_BF420.csv'
# le fichier contient les colonnes Ic et hFE_25
data = pd.read_csv(nom_fichier, sep = ';')
# permet de placer les données du fichier .csv dont les séparateurs sont des point-virgules dans une variable de type dataframe


#Extraction des colonnes du tableau
x = data['Ic(mA)'] # Extraction de la colonne dont le nom dans le tableau est Ic
y = data['hFE_25'] # Extraction de la colonne dont le nom dans le tableau est hFE_25


def funcNonLin(x, a, b, c, d):
return a + b * np.log10(x) + c*x**2 + d*x**3


#color couleur de la courbe ‘b’, ‘g’, ‘r’, ‘c’, ‘m’, ‘y’, ‘k’, ‘w’
plt.semilogx(x, y, 'b-', label='données')


popt, pcov2 = curve_fit(funcNonLin, x, y)
plt.semilogx(x, funcNonLin(x, *popt), 'r-', label='fit: a=%s, b=%s, c=%s, d=%s' % tuple(popt))


# affiche dans la console
print("a: %s , b: %s , c: %s , d: %s" %tuple(popt))


plt.xlabel('Ic')
plt.ylabel('hFE')
plt.legend()
plt.axis((0, 100, 45, 80))
plt.grid(True)
plt.show()

[gts2]

C'est simplement que, comme on est en coordonnée semi-log, prendre un mini à 0, conduit à un mini sur l'axe de log(0) non défini.
Il faut prendre un mini adapté aux données , disons 0,01 soit
plt.axis((0.01, 100, 45, 80))

Remarque, comme ici c'est linéaire, vous pouvez le faire directement sous Excel.