Bonsoir
Plongé dans la physique quantique des champs et la théorie des jauges j'ai l'impression d'avoir différentes définitions du d'alembertien selon les ouvrages. J'aimerai s'avoir quelle est pour vous la définition du d'alembertien.
Perso je pencherai pour :
mais avec un "-" devant le premier terme après l'égalité ?? Hein ? Non ?
Merci pour vos propositions (j'ai un énorme doute tout d'un coup)
Cordialement
-----




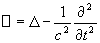


 , qui avec la métrique habituelle +--- te donne bein un signe différent pour le temps et l'espace.
, qui avec la métrique habituelle +--- te donne bein un signe différent pour le temps et l'espace.