réseau et amplitude des maxima

[Bartolomeo]

Bonjour,

Je suis entrain d´étudier les réseaux à l´aide de différents livres (Tipler, Halliday, Orear...). Et j´avoue que je n´ai pas tout compris.
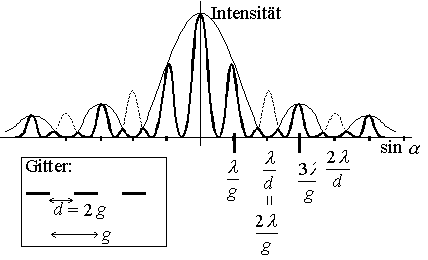
Dans certain bouquins les maxima primaires ont tous la même amplitude. Voici une visualisation avec un applet java: http://www.walter-fendt.de/ph14d/doppelspalt.htm. Dans d´autres livres les maximas ont une amplitude qui diminue avec l´angle de diffraction (elle a l´air modulé avec la fonction d´amplitude d´une fente unique).
Qu´en est il? Quelle est la raison pour laquelle l´amplitude de la lumière passant par un réseau soit modulée par l´amplitude dans le cas de la fente unique? Est-il possible, que dans les livres où l´amplitude de la lumière traversant un réseau est modulé avec la fonction d´amplitude d´une fente, les auteurs sous entendent que la souce lumineuse passe par une fente avant de traverser le réseau?

Cordialement.
-----

[invitea3eb043e]

Un réseau est composé de fentes identiques placées les unes à côté des autres. Chaque fente diffracte la lumière que l'on suppose parallèle (c'est plus simple), ce qui constitue une figure de diffraction. Chaque fente émet avec une phase qui correspond à son milieu. Quand il y a N fentes, ces rayonnements interfèrent. Le résultat est que la figure observée est le produit de la fonction de diffraction par la fonction d'interférence.
Si chaque fente est très fine, la figure de diffraction sera uniforme et on ne la verra pas, c'est pourquoi dans certains cas, on ne parle pas de la figure de diffraction : on suppose les traits infiniment fins.
Quand on éclaire via une fente, la diffraction par cette fente ne joue aucun rôle : la fente sert à créer un faisceau à peu près parallèle grâce à une lentille qu'on ajoute avant le réseau.

[Bartolomeo]

Merci de m´aider!

Un réseau est composé de fentes identiques placées les unes à côté des autres. Chaque fente diffracte la lumière que l'on suppose parallèle (c'est plus simple), ce qui constitue une figure de diffraction. Chaque fente émet avec une phase qui correspond à son milieu. Quand il y a N fentes, ces rayonnements interfèrent.

Ceci est clair pour moi.

Le résultat est que la figure observée est le produit de la fonction de diffraction par la fonction d'interférence.
Si chaque fente est très fine, la figure de diffraction sera uniforme et on ne la verra pas, c'est pourquoi dans certains cas, on ne parle pas de la figure de diffraction : on suppose les traits infiniment fins.

Est-ce alors un effet purement théorique, càd si et seulement si les fentes sont considérées comme infiniment petites? L´intensité de chaque raie est la même pour tout les ordres (considérant une lumière parallèle d´1 seule longueur d´onde) ?

Quand on éclaire via une fente, la diffraction par cette fente ne joue aucun rôle : la fente sert à créer un faisceau à peu près parallèle grâce à une lentille qu'on ajoute avant le réseau.

là je ne comprends pas pourquoi, puisque le réseau n´est pas forcément éclairé avec la même intensité sur toute sa largeur en raison de la diffraction entrainé par la fente d´entrée.


Comment expliquez vous ceci? C´est le graphe de l´amplitude sur un écran d´une lumière monochromatique traversant un réseau:

[invitea3eb043e]

Calculer l'intensité diffusée par un réseau est un vrai challenge qui relève des équations de Maxwell dans le matériau. Pour les besoins de l'optique, on se contente de considérer que chaque élément de fente diffracte la même intensité. C'est une approximation. Pas de raison sérieuse de dire que l'intensité est la même dans tous les ordres.
On évite toujours d'éclairer un réseau directement avec une fente car cela crée des incidences non constantes et ça fait baisser la résolution, on met un objectif pour faire un faisceau parallèle ou presque.
La diffraction de la fente d'entrée ne joue aucun rôle car elle n'est pas éclairée en lumière cohérente.
Dans la figure que tu proposes, on voit bien que le résultat est le produit de 2 fonctions, l'une en sin(x)/x diffraction par une fente de largeur a/2 et l'autre une figure d'interférence de traits distants de a, aussi en sin(x)/x car il n'y a que 2 fentes.

[A voir en vidéo sur Futura]

[Bartolomeo]

Calculer l'intensité diffusée par un réseau est un vrai challenge qui relève des équations de Maxwell dans le matériau. Pour les besoins de l'optique, on se contente de considérer que chaque élément de fente diffracte la même intensité. C'est une approximation. Pas de raison sérieuse de dire que l'intensité est la même dans tous les ordres.
On évite toujours d'éclairer un réseau directement avec une fente car cela crée des incidences non constantes et ça fait baisser la résolution, on met un objectif pour faire un faisceau parallèle ou presque.

Je voudrais comprendre qualitativement: si pour un réseau illuminé par un laser la forme de la fonction d´amplitude est celle du graphe que j´ai inclu; avec plus de maxima biensûr puisque il y a plus de 2 fentes, et étant modulé avec la fonction d´amplitude d´une seule fente (Même s´il n´y a pas de fente avant le réseau).

La diffraction de la fente d'entrée ne joue aucun rôle car elle n'est pas éclairée en lumière cohérente.

En admettant que la fente soit éclairé par un faisceau de lumière cohérante. Que se passe il dans ce cas sur l´écran apres les doubles fentes.

Dans la figure que tu proposes, on voit bien que le résultat est le produit de 2 fonctions, l'une en sin(x)/x diffraction par une fente de largeur a/2 et l'autre une figure d'interférence de traits distants de a, aussi en sin(x)/x car il n'y a que 2 fentes.

C´est le résultat de quoi? Une fente unique éclairée par un faisceau cohérent suivie d´une double fente? Ou bien est-ce uniquement pour une double fente éclairée par une lumière cohérente (laser).

[invitea3eb043e]

Le graphe que tu montres, ce sont les fentes d'Young éclairées par un laser ou bien par une fente, c'est pareil si la fente est assez fine. Il y a 2 fentes.
Si on augmente le nombre de fentes, ça ne change pas l'interfrange, simplement ça affine les pics.
Eclairer une fente source en lumière cohérente ne présente pas d'intérêt. Tout ce que ça peut faire, c'est détruire l'homogénité d'éclairage du réseau.

[LPFR]

Bonjour.
On peut calculer l'image de diffraction d'un réseau en utilisant la transformée de Fourier et le produit de convolution.
C'est moins dur de ce que l'on croit, si on sait ce que veut dire "produit de convolution" et si on sait le faire "à la main".

L'image de diffraction est la transformée de Fourier de l'objet qui "cache" le faisceau incident. On peut faire un parallèle, dans des problèmes comme celui-ci (réseau à une seule dimension) avec la transformée de Fourier en électronique. La seule précaution est que les correspondances sont:
Pour la forme du réseau t <---> x
Pour l'angle de diffraction θ: ω <---> -k sinθ (où k = 2π/λ = nombre d'onde).
Et il ne faut oublier que le θ ne peut pas dépasser 90°!

La transformée de Fourier d'un réseau infini de fentes de largeur 'a' et distance entre fentes 'b', est un ensemble de raies séparées par des fréquences 1/b (en électrique) et dont l'amplitude est modulée (l'enveloppe) par un sinus cardinal avec le premier zéro à 1/a.

Maintenant, si la longueur du réseau éclairée est L, on peut le voir comme le produit d'un signal A qui vaut 1 pour la zone éclairée et zéro ailleurs, multiplié par un réseau infini. Donc, la transformée de Fourier sera le produit de convolution des deux transformées. La première transformée est celle que je viens de décrire, et la transformée du signal A est encore un sinus cardinal, mais dont le premier zéro se trouve à 1/L.

Donc, la transformée d'un réseau fini est formée par des "raies" dont la largeur est 1/L séparées par des fréquences 1/b (qui sont celles de Bragg) et dont l'amplitude est modulée par valeur absolue d'un sinus cardinal dont la largeur est 1/a.

(Quand je dis "largeur d'un sinus cardinal" il s'agit de la position du premier zéro).

Au revoir.