simulation rotation 3 triangles

[invitebc7e8139]

salut tout le monde,

j'ai une petite question:

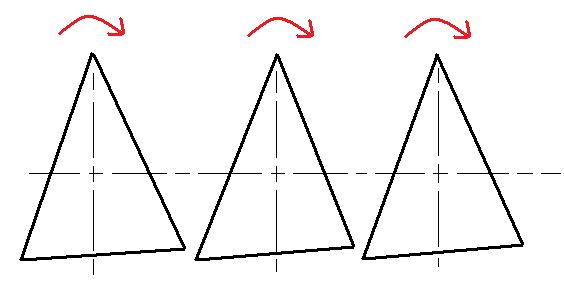
j'ai 3 triangles équilateraux et identiques. La langeur des côtés est de 400mm.
les 3 triangles sont fixés axialement par leurs centres. la distance entre les axes est de 420mm. Ces axes sont parallèles.
Point de depart: les trois triangles ont exactement la même position.
les trois triangles tournent tous en même temps dans le même sens et à la même vitesse.

Question: est ce qu'il va y avoir collision entre ces 3 triangles? "il faut surement faire une simulation mais je n'ai aucune idée comment faire "

Merci d'avance pour vos réponses/aides.
-----

[phys4]

Faut il comprendre que les 3 triangles tournent dans le même plan et que les centres de rotation forment aussi un triangle équilatéral de coté 420mm ?
Si c'est le cas, les cercles tracés par les sommets se recoupent mais les triangles gardent leurs cotés parallèles et je pense qu'ils ne se rencontrent pas , je ne vois pas encore comment le prouver !

[phys4]

J'ai une démonstration possible :
Nous considérons un sommet S et un coté de triangle qui se trouve en face du sommet, soit R la distance du sommet S à l'axe. D la distance des axes.
Nous cherchons pour quel angle S touche le coté en face qui tourne autour de l'axe de son triangle à la distance R/2.
Le rayon du sommet a le même angle que la perpendiculaire au coté. Lorsque S touche le coté nous avons


Si l'angle correspondant au contact est plus grand que 30°, alors le contact aurait lieu au delà du cotée opposé et les triangles ne se touchent pas.
Le coté des triangles
et

Nous obtenons comme limite de contact des triangles D = a, si D > a il n'y a pas collision.

Une petite figure sera sans doute nécessaire ?

[LPFR]

Bonjour.
Je viens de faire les calculs et je suis arrivé au même résultat que Phys4.
Il faut que la distance entre centres soit plus grande que les côtés des triangles.
Au revoir.

[A voir en vidéo sur Futura]

[invitebc7e8139]

merci beaucoup pour vos réponses!

oui les 3 triangles tournent dans le même plan.

J'essaie de suivre tes calculs mais une petite figure ne va me faire que du bien

merci d'avance.

[invitebc7e8139]

re,

voila pour mieux comprendre mon but voici une figure sur laquelle on voit les 3 triangles équilatéraux qui sont et tournent dans le même plan. Les axes des triangles sont alignés et ne changent pas de position.

[phys4]

Bonjour demandeur, que les centres de rotation soient alignés ou non cela ne change rien au problème.
Nous avons déjà beaucoup fait, j'espère que tu trouvera la figure seul.
Essaie d'imaginer deux triangles tournant ensemble.