Bonjour,
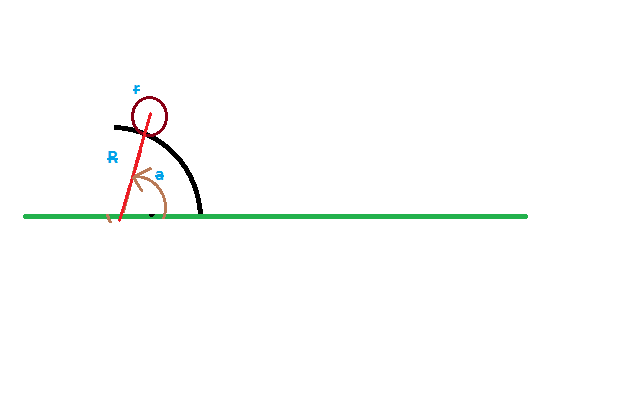
Je me suis intéressé au problème classique suivant: une sphère de rayon r part du sommet d'un quart de sphère de rayon R avec une vitesse initiale nulle. On suppose qu'il y a roulement sans glissement. Déterminer l'angle à partir duquel la sphère décolle du support.
Après étude, je trouve un angle
Je souhaitais savoir si ce résultat est bien juste. Merci d'avance
Bonjour,
Personne ne répond mais moi-même, je ne visualise pas ce problème que vous dites classique ... Peut être un dessin aiderait ?
Voici un dessin de la situation:
XXX pas d'image sur hébergeur externe XXX
(j'ai rebaptisé thêta en a)
Dernière modification par obi76 ; 15/06/2013 à 18h27.
Bonsoir.
Je visualisais bien la situation sauf que j'avais défini l'anglepar rapport à la verticale mais bon...
Pourrais-tu nous indiquer les étapes (pas nécessairement les calculs juste les lois physiques utilisées...) ? Ce qui pourrait être plus utile que le résultat lui-même...
Duke.
Bonjour,
On a décollage dès que la force de réaction (normale à la sphère, si on néglige les frottements) devient nulle.
J'avoue que je n'ai pas vraiment envie de faire les calculs....
@+
Not only is it not right, it's not even wrong!
Bonjour,
petite question auxiliaire : la boule peut tourner sur elle même ? Il faut prendre son moment d'inertie en compte ?
\o\ \o\ Dunning-Kruger encore vainqueur ! /o/ /o/
Y a aucune masse dans le problème, si ?Envoyé par obi76
Non effectivement (en fait je me posais juste la question : si on intègre le moment d'inertie, donc la masse, est-ce qu'elel se simplifie aussi, intuitivement je n'arrive pas trop à voir. Enfin bref c'est un peu HS là).
\o\ \o\ Dunning-Kruger encore vainqueur ! /o/ /o/
Salut,
ton calcul me semble bien compliqué... il me semble que j'avais déjà fait un exercice de ce genre, j'avais fais un truc comme sa:
vecteur P + vecteur N = m x vecteur accélération en tout point
projection sur vecteur n normal à la courbe (repère de Frenet) : -mgcos (alpha) + N = m x accélération normale = m(-v²/R)
En un point quelconque, soit en B (bille quitte la sphère) :
N = -mv(b)²/R + mgcos(alpha)
D'après la variation d'énergie cinétique,v(b)²-v(a)²=2gR(1-cos(alpha))
v(b)²=v(a)²+2gR(1-cos(alpha))
N=-mv(a)²/R + 2mg(1-cos(alpha)) + mgcos(alpha)
Si la bille quitte la sphère, on a N=0, et v(a) vitesse initiale nulle puisque lancement sans vitesse initiale
0=-2mg + 3mgcos(alpha)
cos(alpha)=2/3
Alpha=48,...°
A+
Petite erreur, c'est : N=-mv(a)²/R - 2mg(1-cos(alpha)) + mgcos(alpha)
Parce qu'il y a r, rayon de la bille.
La formule du message #1 semble raisonnable. En tout cas donne des résultats raisonnables aux limites R>>r et R<<r. Faudrait que Nobium nous dise un peu ce qu'il a fait
Re,
oui c'est bien ce que je dis, je ne vois pas en quoi le rayon de la bille change l'angle alpha... ni son poids d'ailleurs...
Mais je me trompe surement
A+
Ah bah si, l'angle de décollage dépend du rayon de la bille...
C'est facile à voir : si la bille est énorme devant le quart de cercle, elle ne décolle jamais (alpha=0 dans les notations du message #3)
Pourquoi ne décollerait-elle jamais ? Le sol qui l'empêche ? Ce n 'est pas dans les conditions
Mon calcul ne tient pas compte du rayon et je trouve une solution, comment expliquer mon résultat alors ? Je me suis trompé ?
Oui excusez moi je vais préciser ma démarche. J'ai considéré que la réaction normale N devait s'annuler, plus précisément la réaction normale comme fonction de l'angle doit s'annuler.
Je considère un repère cylindrique. Le théorème de la résultante dynamique projeté sur le vecteur orthoradial donne une expression de N en fonction de
Pour cela j'ai utilisé la conservation de l'énergie mécanique, qui m'a permis d'exprimer la dérivée en fonction de
J'ai réinjecté dans ma première équation et j'ai trouvé le résultat de mon premier post, indépendant de la masse m de la sphère.
Je pensais que c'était un exercice relativement classique, donc j'ai posé la question sans plus de précision.
Sinon pour Sephiralo, le but de l'exo est justement de ne pas assimiler la sphère à un point matériel donc ce n'est pas si simple malheureusement.
Merci pour vos réponses.
Y a pas de sol dans cette expérience de pensée.Pourquoi ne décollerait-elle jamais ? Le sol qui l'empêche ? Ce n 'est pas dans les conditions
Mon calcul ne tient pas compte du rayon et je trouve une solution, comment expliquer mon résultat alors ? Je me suis trompé ?
Ton calcul est la limite r<<R.
Dernière modification par coussin ; 15/06/2013 à 21h43.
Enfin, théoriquement...
Tu trouves acos(2/3) et la formule du message #1 donne, elle, acos(10/17). Y a ça qui colle pas...
Bonjour.
J'ai pris la peine de faire le calcul et, surprise, l'angle ne dépend ni de la masse ni de 'g' ni des rayons.
Je trouve que l'angle est arcos(7/10) (par rapport à la verticale).
Mais comme je fais souvent des erreurs dans ce type de calcul, je ne parierais pas plus qu'un café.
Si Nobium veut vérifier ses calculs, je l'invite à donner des résultats intermédiaires. Par exemple, la vitesse tangentielle de la sphère en fonction de l'angle thêta.
Au revoir.
Re.
Correction:
Ça dépend quand même du rapport des rayons.
Ça vient de la dépendance entre la vitesse tangentielle et la vitesse de rotation de la petite sphère sur la grande qui n'est pas V/r
A+
Bonjour,
Le problème est traité dans cette discussion :
http://www.les-mathematiques.net/pho...,551151,551152
N'hésitez pas à descendre dans les posts , jusqu'à atteindre la figure en couleurs .
Bonjour Catmandou.
La solution donnée dans le lien est erronée. C'est celle que j'avais calculée en premier.
La vitesse angulaire de la bille n'est pas V/r car la bille tourne en même temps autour du centre de la grande sphère.
La vitesse angulaire est:
Ceci change l'énergie cinétique de la bille en fonction de la hauteur de chute.
Au revoir.
Re.Bonjour Catmandou.
La solution donnée dans le lien est erronée. C'est celle que j'avais calculée en premier.
La vitesse angulaire de la bille n'est pas V/r car la bille tourne en même temps autour du centre de la grande sphère.
La vitesse angulaire est:
Ceci change l'énergie cinétique de la bille en fonction de la hauteur de chute.
Au revoir.
Re-correction.
Finalement la vitesse angulaire est bien V/r.
Mais ce n'est pas évident, comme si la sphère roulait sur du plat. Il faut le démontrer.
On ne peut pas l'affirmer tel quel.
A+
Et apparemment, la différence entre le acos(2/3) et le acos(10/17), c'est les frottements (glisser sans rouler vs rouler sans glisser)
Marrant (et contre-intuitif...) que ce soit finalement indépendant de r
Bonjour et merci pour les réponses. En refaisant le calcul, je trouve une formule différente... Je vais donc expliciter les relations que j'obtiens:
1) Le théorème de la résultante dynamique me donne
2) J'écris ensuite la conservation de l'énergie mécanique. Par commodité, je dois paramétrer la rotation propre de la boule, je le fais à l'aide d'un angle
La conservation de l'énergie s'écrit:
On aboutit alors à
Soit finalement:
Argh! Cette nouvelle formule donne maintenant asin(2/3) pour r<<R (pas acos, asin)
Re,
J'ai de la ressource en matière de recherches ... A défaut de savoir faire les exercices , au moins rapidement ...
Voici la bille qui glisse :
http://e.m.c.2.free.fr/boule-sur-sphere.htm
Alors pour le changement de cos en sin, j'ai l'explication: la première fois que j'ai fait le calcul j'ai pris l'angle
Par contre ça n'explique la forme de l'argument de mes fonctions.
PS: Catmandou, dans ce lien, la boule glisse sans rouler donc le problème n'est pas le même!
