Bonsoir,
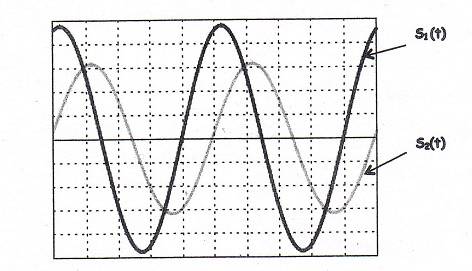
La figure représente un écran d'oscilloscope avec deux signaux sinusoïdaux de même fréquence s1(t) et s2(t). Une division pour l'axe des temps correspond à 20 ms
1) déterminer la fréquence des signaux
2) Calculer le déphasage de s2 par rapport à s1
3) Quelle est la phase de s1 au point le plus à gauche de l'écran
1) f=10hz
2) je ne sais pas comment on fait pour calculer un déphasage
3) je ne vois pas non plus
Bonsoir à toi,
Dans ton cas il n'y a RIEN à calculer, encore faut il savoir ce que veux dire....déphaser et savoir
se le représenter visuellement.
Sais tu ce qu'est le cercle trigonométrique ?
Bonne soirée
Bonjour
Le dephasage est de l'ordre de 72° +/- k (360°)
En science " Toute proposition est approximativement vraie " ( Pascal Engel)
Je ne vois pas à quoi correspond le déphasage >< comment faire avec le cercle trigonométrique?
Sur une période entiere la phase tourne de 360° ou de 2 pi
A = Sin Wt = Sin 2 pi F t
La phase c'est 2 pi F t
Pour une période t varie de T = 1/F
Pour t = 0 la phase est 0
Pour t = T la phase est 2 pi F T =2 Pi 1/T T = 2 pi ou 360°
Lorsque les sinusoïdes sont décalées c'est la phase qui est en avance ou en retard
En science " Toute proposition est approximativement vraie " ( Pascal Engel)
D'accord et comment savoir à quoi correspond le déphasage? je ne vois pas trop
Sut ton oscillo tu vois 2 sinusoïdes
A = a sin Wt et une 2° qui vaut B sin Wt'
Comme l'axe des des temps est le même ( l'axe horizontal) et sur les maximum des sinusoïdes ne se produisent pas au même instant, il faut introduire un déphasage d pour que l'axe des temps soit le même
A =a sin Wt et B = b sin (Wt + d ) d est la valeur du dephasage.
En science " Toute proposition est approximativement vraie " ( Pascal Engel)
Oui mais il varie se déphasage alors? on doit le déterminer avec un modulo 2pi? (je vois pas toujours pas comment on fait pour le trouver ><)
salut,
le déphasage c'est le retard entre 2 courbes:
donc tu prends 2 points sur chacune des courbe facile à repérer ( minimum, 0 ou maximum)
Tu comptes les carreaux entre les abscisses des 2 points ( je l'appel n )et tu divises par le nombre de carreaux d'une période(N)
ensuite tu fais n/N*360 pour avoir le déphasage en degrés
Bonjou r à toi,Envoyé par footderue
Le déphasage correspond à une DIFFERENCE dans la position des signaux à un MEME moment.
Tu peux prendre n'importe quelle position pour un signal et bien sur faudra prendre la MEME position pour l'autre signal.
Si cela ne t'as pas été inculqué durant les cours, c'est sur tu ne peux savoir ce que cela veut dire.
Il est bon de ne pas parler de "retard" , mais de DIFFERENCE si l'on ne sait quel est le signal qui sert de....référence.
Bonne journée
Dernière modification par f6bes ; 09/09/2013 à 08h01.
Est-ce que ça serait 72°?
J'ai n=1carreau et T=5carreaux
Je comprends mieux à quoi ça correspond
Bonjour,
Je pose la question sans malice : 72 ou 288 ° ? Et à k (360°) près ?
Bonjour , tu'as http://fr.wikipedia.org/wiki/D%C3%A9phasage
et http://www.sciences.univ-nantes.fr/s...dephasage.html
on prend l'exemple de deux masses identiques suspendus à deux ressorts identique ,si tu tire et tu lache les deux masse en même temps,leur mouvement est décrite par
x=x(max)cos(wt) ou bien par x=x(max)sin(wt+pi/2)
si tu lache un après l'autre ,tu'aura :
x(1)=x(m)cos(wt) et
x(2)=x(m)cos[w(t-T)] le déphasage est
wt-[w(t-T)]=wT
avec T le retard , tu prend les points d'intersection des deux courbes avec la droite des abcsisses , tu'en déduit le temps T=nbr de carreaux .temps/carreaux.
le déphasage est
wt-[w(t-T)]=wT
Dernière modification par azizovsky ; 10/09/2013 à 05h16. Motif: b
bonjour , tu'as http://fr.wikipedia.org/wiki/D%C3%A9phasage
et http://www.sciences.univ-nantes.fr/s...dephasage.html
on prend l'exemple de deux masses identiques suspendus à deux ressorts identique ,si tu tire et tu lache les deux masse en même temps,leur mouvement est décrite par
x=x(max)cos(wt) ou bien par x=x(max)sin(wt+pi/2)
si tu lache un après l'autre ,tu'aura :
x(1)=x(m)cos(wt) et
x(2)=x(m)cos[w(t-T)]
le déphasage est
wt-[w(t-T)]=wT avec T le retard , tu prend les points d'intersection des deux courbes avec la droite des abcsisses , tu'en déduit le temps T=nbr de carreaux .temps/carreaux.
