Bonjour
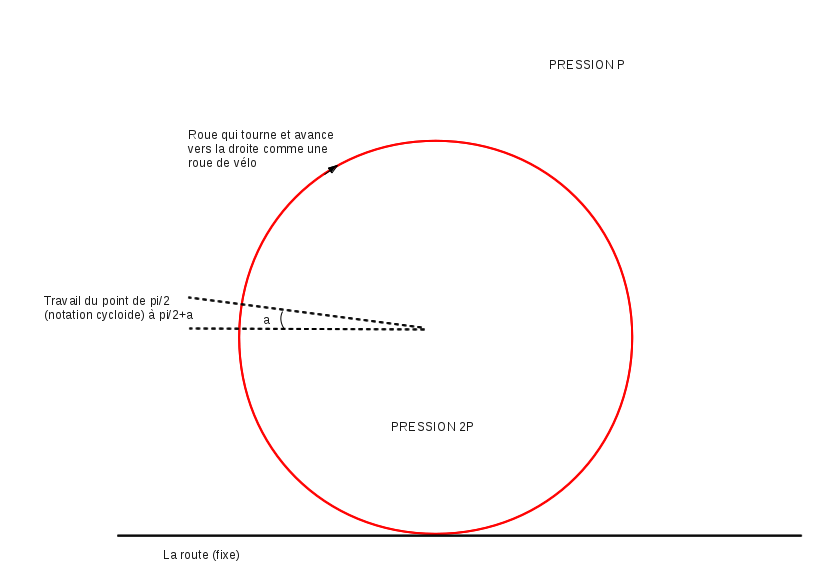
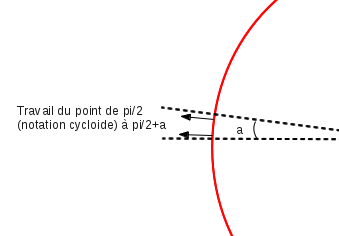
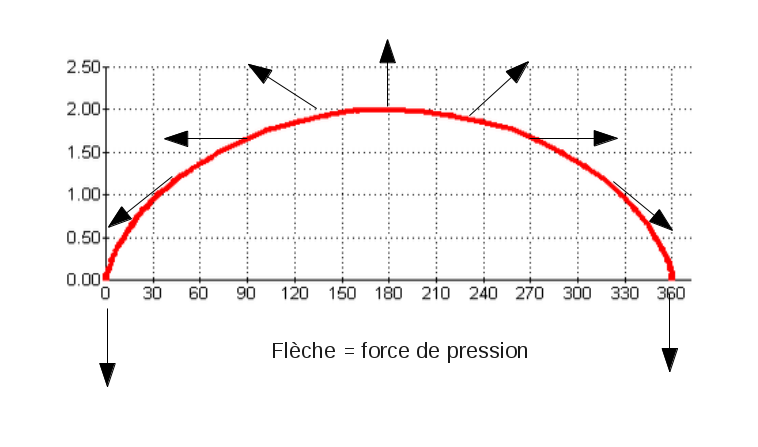
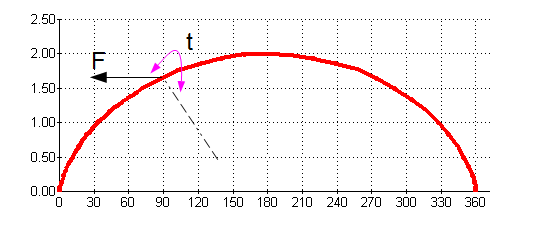
Je souhaite calculer le travail qu'effectue un point sur une roue de vélo qui tourne et avance en translation comme la roue d'un vélo sur la route. Je suppose qu'il n'y a que la pression d'un gaz à l'intérieur de la roue, rien à l'extérieur, chaque point va donc travailler, la somme sera bien entendu nulle sur un tour mais est ce que le travail est cela:
Si je souhaite le travail entre pi/2 et pi/2+angle ?
Merci par avance
Cordialement
Bonjour.
Le travail c’est une force par un déplacement (avec des conditions sur les directions).
Je ne vois pas de quelle force il s’agit
Au revoir
Bonjour LPRR,
La roue possède un gaz sous pression 2P à l'intérieur du cercle (en 2dimensions). Il y a une pression externe au cercle, de P. Donc la force de pression va pousser chaque point du cercle vers l'extérieur. Et comme la roue avance et tourne chaque point devrait fournir un travail positif à un moment et négatif à un autre.
J'ai pris l'équation de déplacement d'un point du cercle (équation paramétrique de la cycloïde) et j'ai multiplié par l'angle (j'ai inversé cos et sin parce que je fait le calcul au alentours de pi/2) mais je ne sais pas si c'est correct ?
Cordialement
En fait comme l'équation de la cycloïde est horaire, je devrais plutôt faire cela :
Si vous avez une idée du calcul exact ?
Il n'y a pas de force externe au système, donc pas de travail.
Imagine que tu es debout au fond d'un bus (à l'intérieur) et que tu pousses constamment sur la vitre arrière. Crois-tu que cette force développera un travail lorsque le bus se déplacera sur la route?
Non, si je calcule l'ensemble des travaux sur tout le cercle alors le travail est nul, bien entendu. Mais je veux connaître l'expression de l'intégrale à calculer pour savoir si j'ai compris comment faire pour ce cas particulier: pour un point uniquement sur un petit angle.
Cordialement
Re.Envoyé par xt63
Dans ce cas prenez un exemple plus « réaliste ». Par exemple, imaginez un « truc » collé sur le côté du pneu qui subit une force de freinage aérodynamique que vous pouvez choisir, constante, proportionnelle à la vitesse ou au carré de la vitesse.
A+
C'est ce calcul que je souhaite faire, pour un point sur un petit angle, c'est plus compliqué que je ne l'ai écrit ?
Le travail c'est la somme des intégrales suivantes ?
C'est bien la distance fois le cosinus de l'angle fois la force. J'ai pris un rayon de 1 et une pression de 1 pour simplifier.
Cordialement
Re.
Désolé, mais moi, sans un dessin indiquant, pour un point quelconque, la force et le différentiel de distance, je ne sais pas faire.
http://forums.futura-sciences.com/ph...s-jointes.html
A+
Voilà pour le dessin:
C'est la différence de pression que j'ai pris à 1. Les équations de la cycloïde sont horaire et avec un décalage de pi/2, donc j'ai essayé de corrigé dans mes intégrales. Pour moi l'angle évolue en horaire selon la cycloïde mais ça ne doit pas changer le résultat.
Cordialement
Re.
Votre dessin n’est pas le bon :
- il n’est pas fait pour un point quelconque : pas de position dans un angle multiple de 45°.
- Vous n’avez pas dessiné la force.
A+
Si le calcul est correct de pi/2 à pi/2+a je pourrai le faire pour n'importe quel point je pense.
J'ai dessiné 2 forces à 2 endroits différents pour montrer les angles:
Cordialement
Re.
C’est toujours un mauvais angle (cas particulier).
Tel que vous avez fait le dessin le déplacement du point d’application de la force est perpendiculaire à celle-ci.
Donc le travail est nul.
Et avant de continuer, je veux l’assurance qu’il ne s’agit pas d’un mobile perpétuel (énergie gratuite, sur-unitaire, etc.). Dans cette saison, les hirondelles s’en vont et sont remplacées par des mobiles perpétuels.
A+
Non, ce n'est pas un mobile perpétuel, il est évident que le calcul sur le cercle complet fera 0. Sinon, ce serait les cyclistes du tour de France qui seraient contents !
Oui, j'ai du mal à dessiner la force, car la roue tourne mais elle avance aussi, la force de pression est toujours perpendiculaire à la paroi ? C'est pour cela que j'ai dessiné la force comme cela par contre le cercle ne fait pas que tourner, il avance aussi en translation, donc il y a un travail sur x et sur y, comment dessiner la force autrement ?
Cordialement
Re.
Dans ce cas je ne vois pas d’où sortent vos intégrales. Sont-elles tombées du ciel ? Un copain vous les a données ?
C’est à partir du dessin (éventuellement dans sa tête) que l’on peut écrire le différentiel du travail et mettre un signe intégral devant.
Dessinez l’épicycloïde et la roue dans un point QUELCONQUE. Vraiment quelconque. Choisissez par exemple une situation dans laquelle le point en question se situe sur un rayon qui fait quelques 30° avec l’horizontale.
Là, vous pourrez dessiner la force (radiale que vous avez choisi) et le dℓ (le long de l’épicycloïde). Débrouillez vous pour calculer le produit scalaire (ou pour trouver l’angle entre la force et le dℓ).
A+
Le problème tel que tu le poses reviens à calculer le travail de la force exercée par un ressort qui ne se détendrait pas, mais enfin bref...
Alors voilà, pour le calcul de la longueur du segment j'ai utilisé la racine carré de la somme des carrés des dérivées, ensuite pour l'angle de tangente j'ai utilisé la division de la dérivée dy/dx et finalement pour l'angle final, eh bien, il faut que je traite 2 cas, entre 0 et pi et entre pi et 2pi, je ne sais pas faire pour tout le segment uniquement de 0 à 2pi, je ne m'en sort pas avec les tangentes.
Equations de la cycloïde:
Alors le calcul de la longueur du segment :
La dérivée de x donne:
La dérivée de y donne:
Donc la longueur du segment est:
Pour la tangente au point, j'ai utilisé la formule dy/dx:
Maintenant, il faut trouver la perpendiculaire car la force de pression est perpendiculaire à la surface:
Pour la différence entre les angles, je n'ai pas trouvé de simplification et donc la formule fonctionne de 0 à pi (mais je cherche autour de pi/2), il faut décaler avec l'angle que fait la force :
Si pouvez me dire si c'est bon ou pas ?
Cordialement
Si je pose :
alors c'est valable pour tous le cercle.
Si quelqu'un peut vérifier svp ?
Bonjour,
J'ai fait le calcul pour un point quelconque pour intégrer de
J'ai bien 0 sur un tour.
On peut simplifier L:
J'ai deux questions:
1/ est ce correct ?
2/ j'ai calculé le travail pour un point mais si je veux calculer le travail pour une surface je dois multiplier le résultat de l'intégrale par la profondeur et par la longueur du segment ?
Cordialement
J'ai fait l'image pour montrer les forces de pression tous les 45°
Cordialement
Bonjour.
Votre dessin artistique est plutôt inexacte et surtout inutile. Il ne permet pas de calculer
Je vous ai dit ce qu’il faut faire. La suite ne dépend que de vous.
Au revoir.
Bonjour,
J'ai refait le dessin en montrant pour le point pi/2 la force de pression, la perpendiculaire à la surface et l'angle t'. L'angle est de:
P est défini dans un précédent message, c'est la pente.
C'est correct ?
J'ai une question plus globale, une fois que j'aurai le travail d'un point entre 0 et 0.1 rd par exemple, je dois intégrer à nouveau pour connaitre le travail sur l'arc complet, c'est bien cela ?
Cordialement
Bonjour.
Nom d’une pipe !
Dessinez une roue. Choisissez un point dont le rayon qui fait quelques 30° avec l’horizontale.
Dessinez la cycloïde qui passe par ce point et qui correspond au rayon de la roue.
Dessinez la force
Il s’agit de calculer maintenant
Ce
Exprimez ‘x’ et ‘y’ en fonction de l’angle choisi pour décrire la courbe.
Calculez
Calculez le produit scalaire
Simplifiez s’il y a lieu.
C’est ça qu’il faut intégrer.
Au revoir.
