Bonjour,
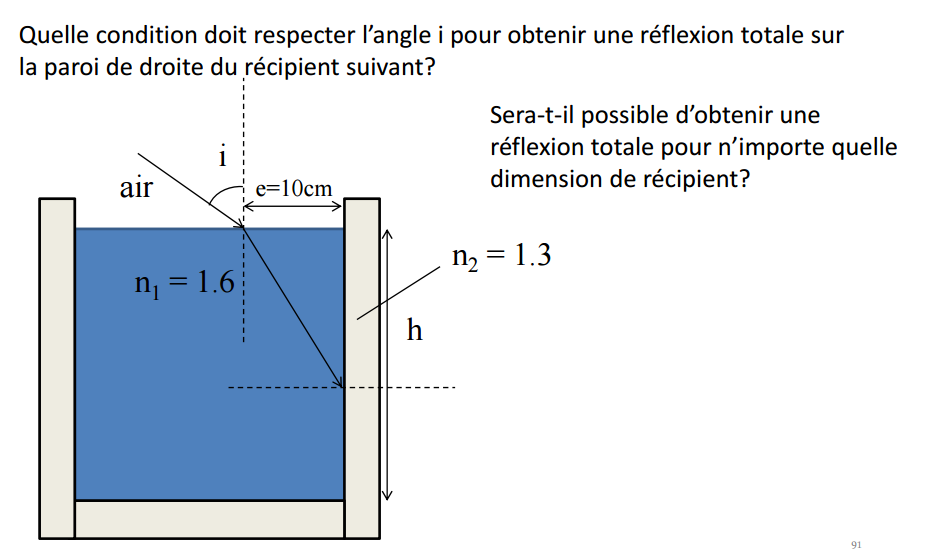
Je sollicite votre aide pour m'aiguiller sur cet exercice théorique sur la réflexion totale:
Pour la première question:
Je dirais que la condition serait que l'angle i2 (angle du deuxième rayon incident) atteigne un angle limite (icritique), on est dans un système où n1>n2, mais alors quelle est la condition pour permettre le premier rayon incident de former un angle i qui permette la réflexion totale du rayon incident 2 (qui est le rayon réfracté)?
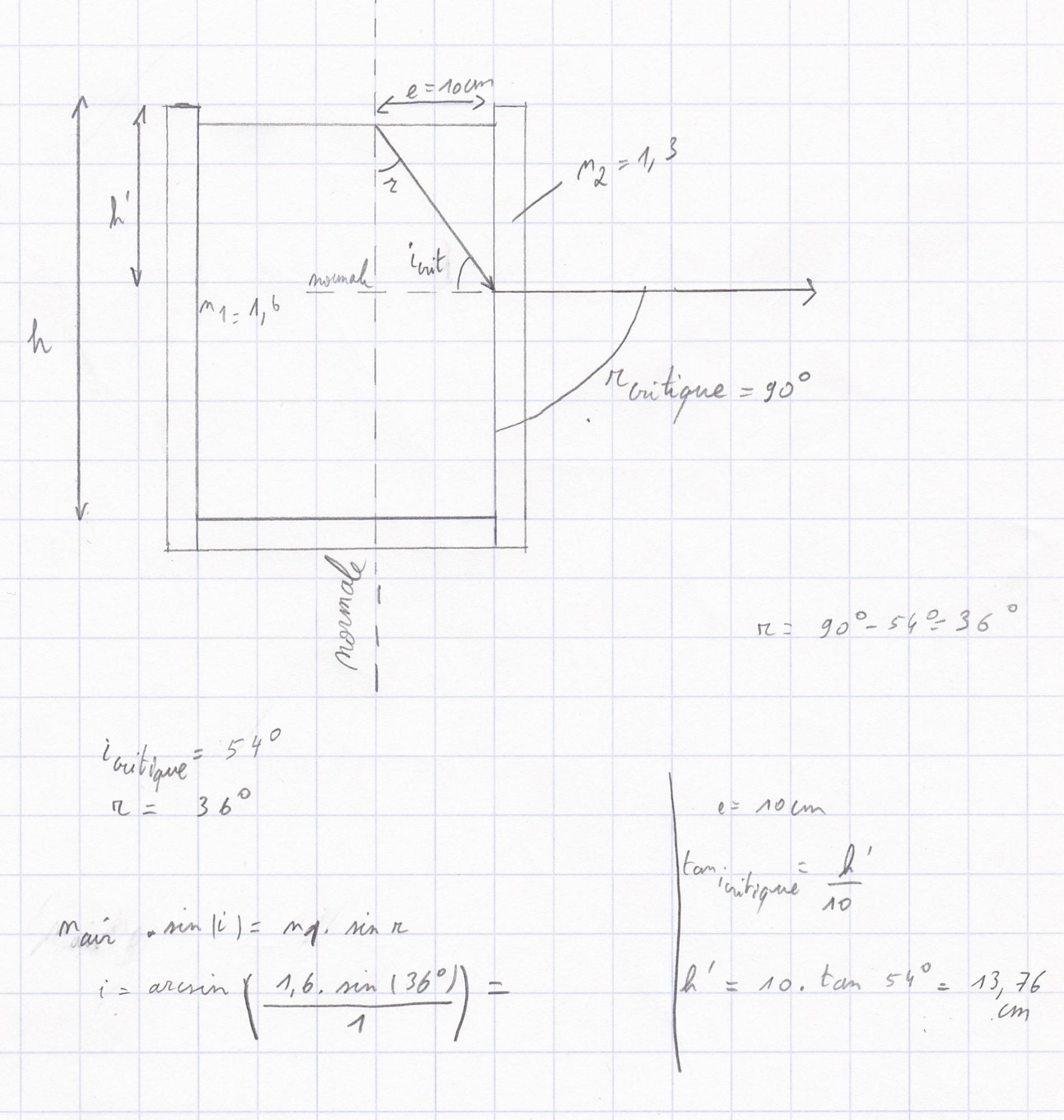
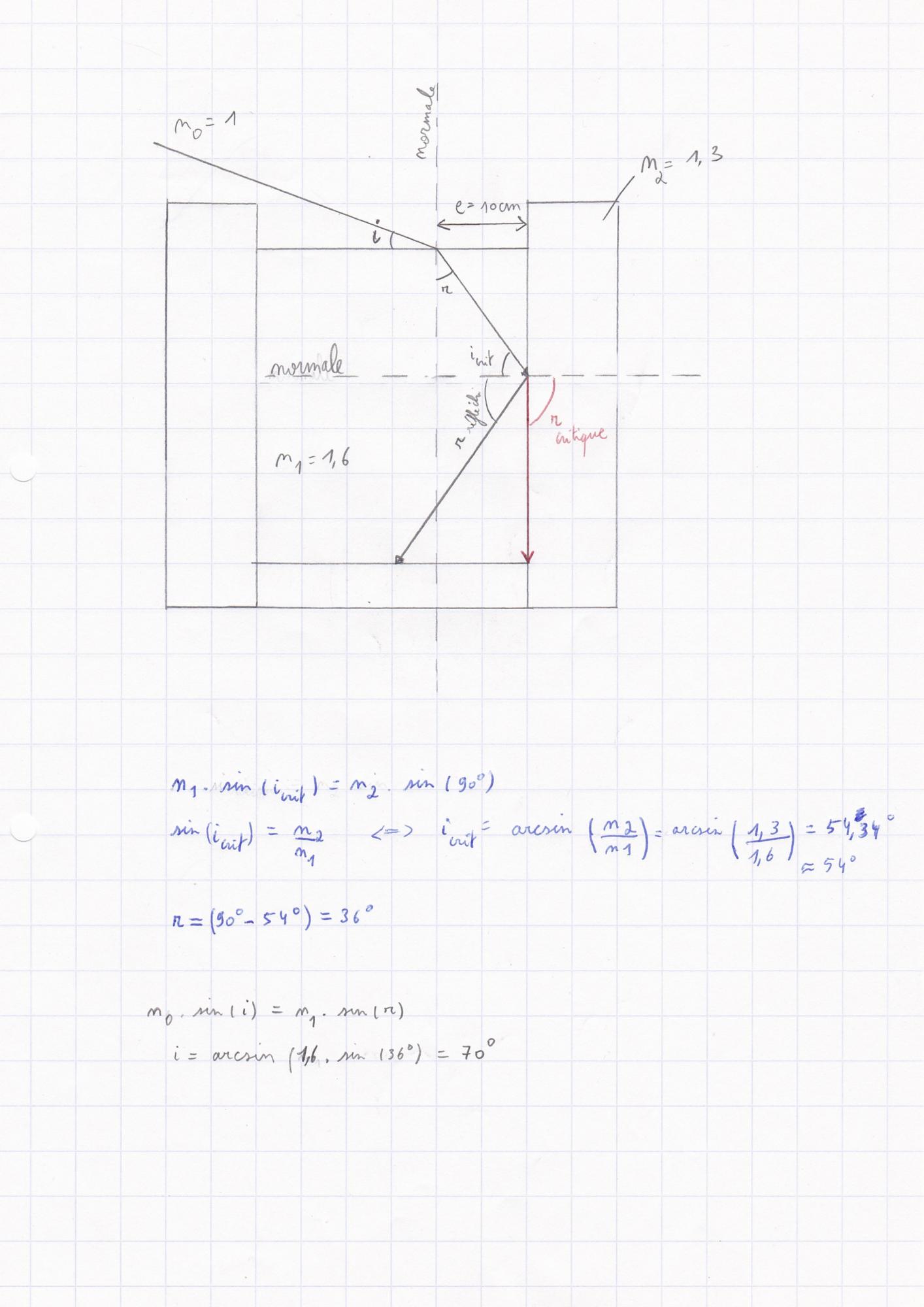
J'ai fait le calcul pour trouver icritique=54° et je présume que r vaut donc également 54°.
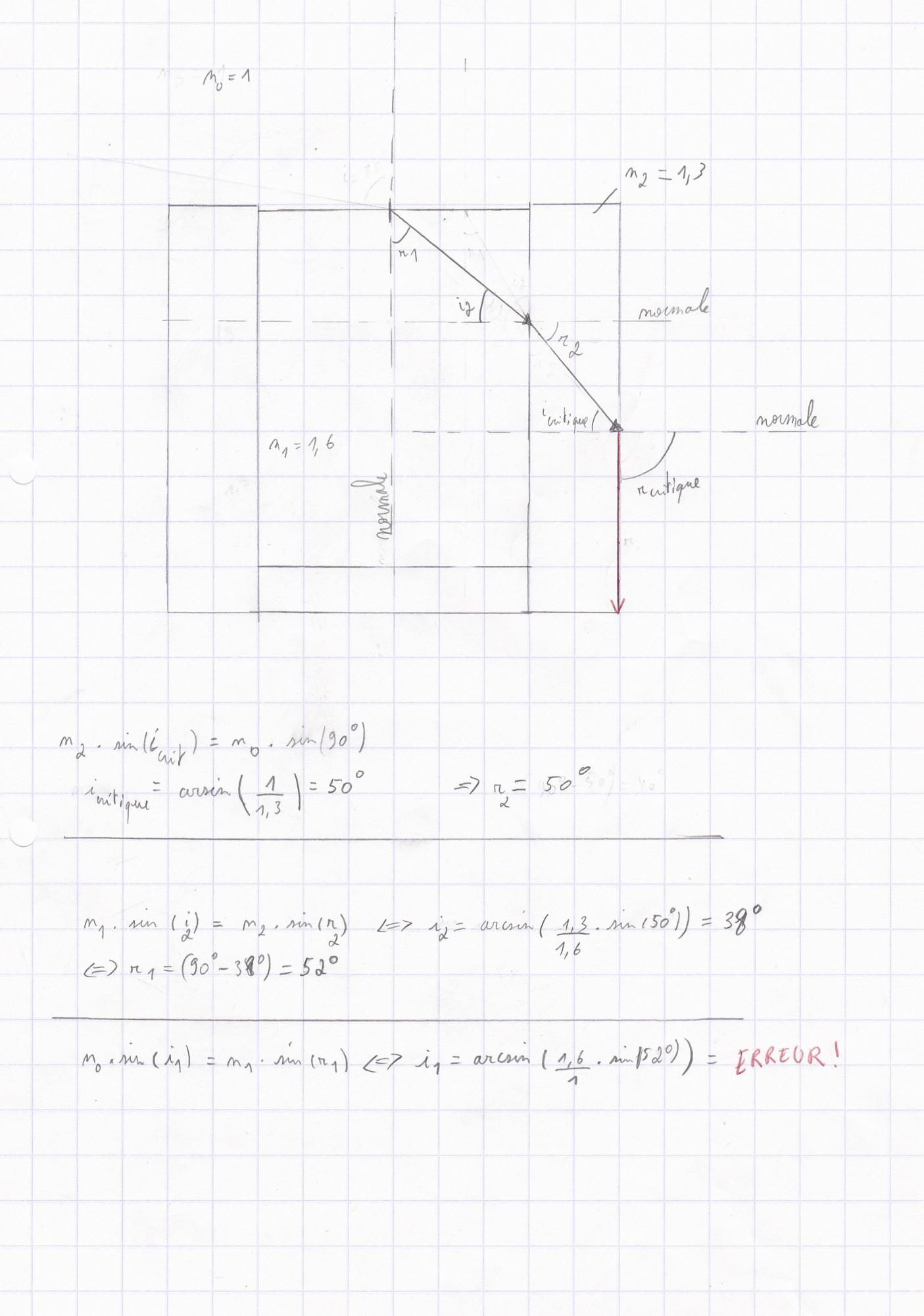
Mais après cela, pour trouver l'angle i, j'ai appliqué la formule i=arcsin (1,6 x sin54°) et j'ai une erreur sur ma calculatrice. Qu'est ce que cela pourrait bien signifier?
Pour la deuxième question:
Je dirais que non, plus l'espace (e=10cm) est grand plus l'angle d'incidence sera grand (comparé à l'angle icritique, i>icritique) et donc tout le rayon incident sera réfléchi, par contre plus l'espace est petit, plus l'angle d'incidence sera grand (comparé à l'angle icritique, i<icritique) et les rayons seront réfléchis et réfractés.
Merci d'avance
-----