Travail effectif maximal récupéré lors d'une détente de gaz

[invite785e8abb]

Bonjour,

J'essaye d'estimer en première approche l'énergie mécanique maximale récupérable par détente d'air comprimé sur un piston avec les hypothèses suivantes :

- L'air se comporte comme un gaz parfait
- Ma détente se passe dans un cylindre totalement perméable thermiquement et est suffisamment lente pour être considérée isotherme (le milieu environnant est suffisamment grand pour que sa pression, P2, et sa T° ne soient pas affectés par la transformation)

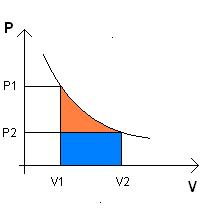
Soient les deux états, initial (P1,V1,T,n) et final (P2, V2, T, n).
La loi de conservation d'énergie veut que DU=0=W+Q avec W=-P1*V1*ln(P1/P2)

Dans ces conditions, et si jusqu'ici je ne me suis pas encore trompé, j'ai deux questions :

a/ Le travail W est le travail exercé par les chocs sur une face du piston au cours de son déplacement. Mais le travail mécanique effectif que je peux récupérer doit tenir compte du travail nécessaire pour vaincre la pression ambiante au long du déplacement de l'autre côté du piston ? Alors Weff=W-Wpext=W-P2*(V2-V1) où le terme W tient déjà compte de cette pression ambiante ?
b/ En prenant cela en compte, comment se détaille la loi de conservation d'énergie DU=Weff +Q ou toujours DU=W+Q ? Accessoirement je voudrais aussi savoir s'il y a un moyen de trouver Q par un autre moyen que Q=-W (avec Q=mCpDT ? Quelle masse m ? Quelles températures).

J'espère beaucoup de vos réponses, n'hésitez pas à me dire si je ne suis pas assez clair dans mes questions,

Bien à vous
-----

[invite785e8abb]

Malgré les vues, je constate que mon sujet est le seul qui reste sans réponse. J'en déduis que mes questions ne sont pas très claires mais j'aurais besoin d'une piste pour expliciter mieux.

Un grand merci par avance

[invite785e8abb]

Je vais simplifier ma question en essayant d'aller à l'essentiel de ce que je n'arrive pas à comprendre.

Dans wiki il est dit au sujet d'un processus isotherme :
"Le calcul du travail en thermodynamique correspond au changement d'énergie potentielle entre l'état en A et celui en B" et que "Pour un processus isotherme réversible, ceci correspond à l'intégrale de l'aire sous la ligne isotherme représentée par un T donné dans le diagramme[...]"

Pour moi, le travail dont il est question est le travail exercé par le gaz parfait sur le système environnant. Une partie sert à vaincre la pression environnante (bleue) et l'autre que j'appelle Weff peut être récupérée mécaniquement (orange) cf schéma :



Suis-je à côté de la plaque en écrivant W = Weff + Wext ? Je me pose la question car je n'arrive pas à associer cela au principe de conservation de l'énergie.

[phys4]

Bonjour,

Votre intervention était passé inaperçu, votre calcul de W est parfaitement exact avec vos hypothèses.
La quantité de chaleur est égale au travail puisque la température du gaz ne change pas, l'énergie provient de la chaleur extérieure.

Il faut retirer le travail fourni par l'autre face du piston ( énergie rendue à l'extérieur), car le cycle est ouvert avec une seule détente.
Dans un cycle fermé l'on n'en tient pas compte car le travail est restitué au retour du piston.

Au revoir.

[A voir en vidéo sur Futura]

[invite785e8abb]

Merci phys4 pour votre réponse !

Alors je peux écrire la loi de conservation Weff+Wext=-Q.

Y-a-t'il un moyen de déterminer Q en passant plutôt par mCpDT (où peut-être DT serait la différence entre T1 et une température T3 obtenue par la détente adiabatique de cette même réserve ?)

Merci

[phys4]

La conversation de l'énergie totale est toujours vraie.

Il faut savoir comment vous définissez Q ?
Dans votre premier message Q est la chaleur qui traverse la paroi du cylindre, différente de la chaleur totale échangée avec l'extérieur puisque qu'une partie est rendue par le déplacement du piston qui chasse l'air extérieur?

La détente adiabatique ne fournira pas le même travail, et il n'y aura pas de chaleur échangée par définition.

[invite785e8abb]

Je voudrais écrire la loi de conservation de l'énergie appliquée à mon système (n moles d'air) en détaillant un maximum les termes.

Si je comprends votre dernier message, le travail mécanique rendu par l'air extérieur à mon système doit correspondre à une chaleur rendue par le système à l'extérieur :

DU=0=W+Q=Weff+Wext+Qeff+Qext avec Qext=-Wext et Qeff=-Weff et Q(chaleur totale échangée entre le système et l'ext)=Qext+Qeff ?

[invite785e8abb]

Bonjour, y aurait-il une bonne âme pour confirmer/infirmer ma dernière conclusion ?

Merci

[phys4]

Bonjour,
J'étais absent une dizaine de jours, et je vois que personne n'a relu vos propositions.

Tout cela manque de clarté, il faudrait bien définir chacune des quantités que vous utilisez et expliciter davantage votre calcul et son but .
Bon courage.