Calcul du coefficient de transmission dans l'effet tunnel.

[AdrienDds]

Bonjour,

Je suis étudiant en 2e année de licence de Physique et nous devons mener un projet de physique. Le notre porte sur l'effet tunnel. Notre problème est que nous n'arrivons pas à calculer le coefficient de transmission. Nous connaissons l'expression (grâce à Internet) mais nous n'avons jamais réussi à le démontrer ou à trouver une démonstrastion. Je vous décrit notre système.

Soit une particule de masse m est d'énergie E arrive des x négatifs vers une barrière de potentiel de largeur a et d'energie Uo ( Uo>E).
Soient les régions 1,2 et 3 tq : La région 1 va des x=-inf jusqu'à x=0
La région 2 de x=0 à x=a ( La barrière de potentiel )
La région 3 de x=a jusqu'à x=+inf.

Grâce à la résolution de l'équation de Schrödinger, nous déterminons les expressions des 3 régions :

ψ1(x) = Aexp(iKx) + Bexp(-iKx)
ψ2(x)= Mexp(k'x) + Nexp(-k'x)
ψ3(x)= Cexp(iKx)+Dexp(-iKx)

Avec :
K=(2mE)^(1/2)/hbarre
k^'=((2m〖(E-Uo))〗^(1/2))/hbarre

Avec les conditions de continuités, on en déduit 4 relations :

A+B=M+N
Ki(A-B)=k’(M-N)
Cexp(iKa)=Mexp(k’a)+Nexp(-k’a)
iKCexp(iKa)=k’(Mexp(k’a)-Nexp(-k’a))


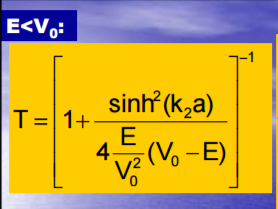
On sait que le coefficient de transmission est défini par T=C/A. Pouvez vous, s'il vous plait, nous donner la méthode pour ce calcul afin que nous puissions continuer notre projet ?

Merci !
-----

[LPFR]

Bonjour et bienvenu au forum.
Le coefficient de transmission est exp(k’a) (avec le signe de k’ que vous avez choisi).
Car dans la barrière de potentiel l’exponentielle doit être décroissante.
Au revoir.

[AdrienDds]

Bonjour, merci de votre réponse !

Je crois que vous m'avez donné l'expression du coefficient de transmission entre II et I. Cependant, et je n'ai pas été explicite, je souhaitais retrouver l'expression entre III et I. Je sais qu'elle ne contient de exp(-k'a).

Cordialement

[curieuxdenature]

On sait que le coefficient de transmission est défini par T=C/A.

Bonjour

je ne sais pas si ça va t'aider mais c'est plutôt T= |A3|² / |A1|²
et il n'y a plus d'exponentielle en effet mais on se retrouve avec un sinh² à simplifier.

Quand vous aurez terminé, en application numérique pour E = 1 eV et Uo = 2 eV vous devez vérifier que
T ~ 0.17 pour un électron (transmission possible) et
T ~ 2.7 10^-57 pour un proton (transmission quasi impossible).

[A voir en vidéo sur Futura]

[AdrienDds]

Oui ! Après relecture de mon post je me suis trompé ! Les termes sont au carré normalement.

Vous avez raison il y a un sinh² dans l'expression. Voici la vrai expression que je dois normalement retrouver :



Avec Vo=Uo et k2=k'

Il me faut juste la méthode pour le retrouver...

Merci !

[curieuxdenature]

Bonjour

A ce que j'ai compris, des 4 équations on doit trouver l'expression suivante:


comme l'affichage du développé est assez fouilli voici le code que j'ai utilisé avec wxMaxima :

/* avec wxMaxima version 16 (gratuit) */
kill(all) $
numer : false $ /* faire passer à true pour appli numérique */
ratprint : false $
simp : true $
fpprec : 99 $
fpprintprec : 14 $
%iargs:true $

print("Taux de transmission barrière de potentiel") $

/* cos(i * phi) =     cosh(phi) = 1/2 * (exp(phi)+exp(-phi)) */
/* sin(i * phi) = i * sinh(phi) = 1/2 * (exp(phi)-exp(-phi)) */

A1 = A3 * exp(%i * k * L) * (cosh(kp * L) + %i * sinh(kp * L) * ((kp^2 - k^2)/(2 * kp * k))) ;

/* m    : 1.672621898 * 10^-27 ; */

/* ligne à supprimer si appli numérique
print("------codata 2014------") $
J_eV : 1.6021766208 * 10^-19 $
m    : 9.10838356 * 10^-31 ;

Vo   : 2 * J_eV ;
E    : 1 * J_eV ;
hbar : 1.0545718 * 10^-34 $
L    : 3 * 10^-10 ;
k    : sqrt(2 * m * E ) / hbar ;

if Vo = E then Vo : E * 1.01 $
if Vo > E then kp : sqrt(2 * m * (Vo - E)) / hbar else kp : sqrt(2 * m * (E - Vo)) / hbar $
ligne à supprimer si appli numérique */

print("---------- 1 ----------") $
/* resultat correct */
A3    : exp(%i * k  * L)  ;
A1    : ratsimp(cos(%i * kp * L) +      sin(%i * kp * L) * (kp^2 - k^2) / (2 * kp * k)) ;
T2    : cabs((A3 / A1)^2) ;

print("---------- 2 ----------") $
/* verifs */
cos(%i * kp * L) ;
sin(%i * kp * L) ;
k  : sqrt(2 * m * E ) / hbar $
kp : sqrt(2 * m * (Vo - E)) / hbar $

T2 : (4 * k^2 * kp^2 / ((kp^2 - k^2)^2 * sinh(L * kp)^2 + 4 * k^2 * kp^2 * cosh(L * kp)^2)), ratsimp ;

print("décomposition des variables de T2)") $
A : 4 * E * (Vo - E) ;
B : (Vo^2 - 4 * E * (Vo - E)) * sinh(L * kp)^2 ;
C : (4 * E * (Vo - E)) * cosh(L * kp)^2 ;
T2 : A / (B + C) ;

print("identique simplifié (cosh est éliminé)")$
A : 4 * E * (Vo - E) ;
B : Vo^2 * sinh(L * kp)^2 ;
C : 4 * E * (Vo - E) ;
T2 : A / (B + C) ;

print("---------- 3 ----------") $
/* resultats après simplifications */
T  : (4 * E * (Vo - E) / ( Vo^2  * sinh(kp * L)^2 + 4 * E * (Vo - E) )), rat ;
print("-----------------------") $
T  : 1 / ( (Vo^2  * sinh(kp * L)^2 / (4 * E * (Vo - E))) + 1 ), rat ;

le résultat abouti bien à



une application numérique donne les résultats que j'ai d'un exercice (sans développement malheureusement)

Barrière Vo = 2 eV
Energie cinétique E = 1 eV
Epaisseur de la barrière L = 3 Angstroems

T pour l'électron ~0.17
T pour un proton ~2.7 10^-57 (si mp=1.67 10^-27 kg)

A vous la balle...