Calculer le transfer de chaleur d'un objet dans le vide de l'espace

[RomVi]

Merci Plumbus pour tes explications, c'est très précis.
J'ai bien aimé l'espuce!
Mais c'est curieux que tu cherches absolument à me proposer les calculs pour un astronaute dans le vide.
Alors que j'aimerais savoir comment on détermine le temps qu'il faut pour qu'un objet placé dans le vide de l'espace atteigne l'équilibre thermique avec son environnement...en négligeant le rayonnement d'un corps proche: soleil, étoile, planète etc...
J'ai l'impression que c'est pas très facile à calculer.
Merci.

je t'ai répondu dès mon 1er message :
On calcule la puissance émise en fonction de la température de surface = emisivité x constante de SF x surface x température^4
Cette puissance permet de calculer la perte en température, connaissant la masse et le CP de l'objet.
-----

[Youri Gagarine]

mais tu l'as dès le post#5, sous réserves :
- de remplacer sigma par sigma . émissivité (merci Romvi)
- qu'on néglige toute source externe de rayonnement (donc le seul phénomène à considérer et le rayonnement de l'objet qui se refroidit)
- qu'on puisse supposer que le corps a une conductivité thermique suffisante pour que sa température soit homogène et le reste durant le refroidissement, comme par exemple ta demande initiale concernant une boule de métal.

sinon, c'est plus compliqué comme l'a dit plumbus par exemple post #25

T, T0, T1 = températures
Cp = capacité calorifique P constant
S = surface
M = masse

Merci pour votre aide.
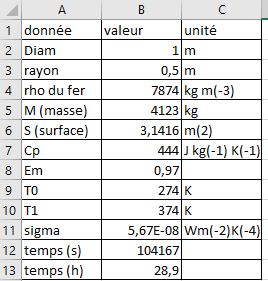
J'arrive à ce résultat:


Sphère métallique de 1 m de diamètre
T₀ = +100°
T₁ = 0°

Cp fer: 3 496 kJ m⁻³ K⁻¹
Emissivité: 0,97
M: 0,523 m³
S: 0,785m²

T= 421 371 sec
115 heures
c'est possible?

[Youri Gagarine]

Erreur dans mes données:

Sphère métallique de 1 m de diamètre
T₀ = +101°
T₁ = 1°

Cp fer: 3 496 kJ m⁻³ K⁻¹
Emissivité: 0,97
M:1570 Kg
S: 3,14m²

T= 600 687 sec
167 heures
c'est possible?

[jacknicklaus]

c'est possible?

non . beaucoup d'erreurs dans tes données. et tu as oublié l'émissivité dans la formule.

[jacknicklaus]

Nota, dans le cas d'une sphère de rayon R, on peut simplifier :



où cette fois :
Cp = capacité thermique volumique = 3496000 Joules par (mètre cube . Kelvin) pour le fer
R = rayon de la sphère
epsilon = émissivité = 0.97
sigma = 5.67 10(-8) W m(-2) K (-4)
et les températures toutes en Kelvin, bien sûr.

On voit que le temps est proportionnel au rayon. une sphère de 10cm se refroidit 10 fois plus vite qu'un sphère de 1 m.

[Youri Gagarine]

non . beaucoup d'erreurs dans tes données. et tu as oublié l'émissivité dans la formule.

Pièce jointe 360050

UN grand marci Jack, maintenant j'y vois plus clair.

[RomVi]

Nota, dans le cas d'une sphère de rayon R, on peut simplifier :



où cette fois :
Cp = capacité thermique volumique = 3496000 Joules par (mètre cube . Kelvin) pour le fer
R = rayon de la sphère
epsilon = émissivité = 0.97
sigma = 5.67 10(-8) W m(-2) K (-4)
et les températures toutes en Kelvin, bien sûr.

On voit que le temps est proportionnel au rayon. une sphère de 10cm se refroidit 10 fois plus vite qu'un sphère de 1 m.

Cette formule ne fonctionne pas, puisque la température de l'objet diminue le rayonnement aussi.
Par ailleurs l'emissivité prise en compte n'est pas réaliste.

[jacknicklaus]

Cette formule ne fonctionne pas, puisque la température de l'objet diminue le rayonnement aussi.
Par ailleurs l'emissivité prise en compte n'est pas réaliste.

oui, mais c'est déjà pris en compte; (calcul d'intégrale post 32); La version post 35 n'est qu'une simplification après calcul d'intégrale du terme M/S dans le cas d'une sphère homogène

quant au 0.97, j'ai repris la valeur de Youri Gagarine. je n'en connais pas l'origine.

[RomVi]

En effet, j'avais regardé un peu trop vite...

[jacknicklaus]

Par ailleurs l'emissivité prise en compte n'est pas réaliste.

tu as raison. j'ai trouvé ceci : (http://www.infrared-thermography.com/material.htm)

Iron, cast, casing
0.81

Iron: cast, polished
0.21

Iron: cast, oxidized
0.64
Iron: hot rolled
0.77

Iron: oxidized
0.74

Iron: sheet, galvanized, burnished
0.23

Iron: sheet, galvanized, oxidized
0.28

Iron: sheet, heavily rusted
0.69

Iron: shiny, etched
0.16

Iron: wrought, polished
0.28


ca joue dans une plage large d'un facteur 3. Le plus haut cité dans l'article en lien, pour le fer, est 0.81. Donc faut augmenter le temps de 20%, au moins.