Bonjour,
J'ai une question concernant l'expression de la densité de flux thermique...Je tombe sur un pseudo-paradoxe :
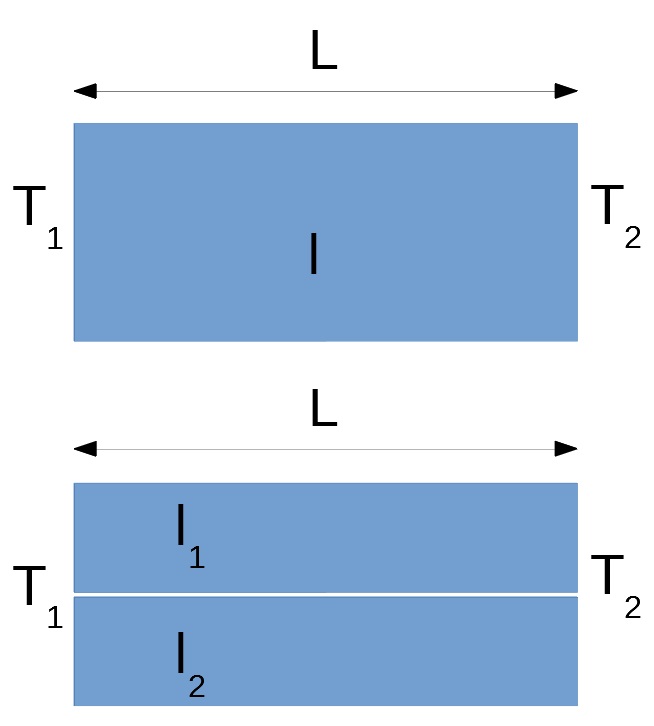
1) Considérons deux plaques 1 et 2 horizontales de longueur L et de conductivités thermiques l1 et l2. Ces deux plaques sont posées l'une sur l'autre et soumises à la température T1 à gauche et à la température T2 à droite (T2 < T1). Le flux se propage selon la longueur des plaques. Ces plaques sont montées en parallèles.
On a :
- résistance thermique de la plaque 1 : R1 = L/l1.
- résistance thermique de la plaque 2 : R2 = L/l2.
Donc : résistance équivalente : Req = R1.R2/(R1+R2) = L/(l1 + l2).
Donc : densité de flux thermique = (T1-T2)/Req = (T1-T2)(l1+l2)/L.
Si maintenant on suppose que les deux plaques sont identiques (l1 = l2 = l), on obtient :
densité de flux thermique = (T1-T2)2l/L.
Si les deux plaques sont identiques, il me semble que tout se passe come si on avait une seule et même plaque de longueur L et de conductivité thermique l (on a le même matériaux de part et d'autre de la zone de contact). Dans ce cas, on trouve : densité de flux thermique = (T1-T2)l/L.
Comme se fait-il que l'on ne retrouve pas l'expression précédente ? Ce problème n'apparaît pas si on considère le flux thermique où la surface transversale des plaques intervient. Comme le flux se propage selon la longueur, l'épaisseur des plaques n'intervient pas ici.
-----