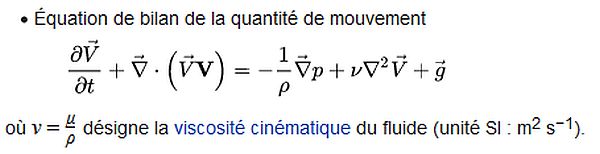Problème de Navier stokes.

[Anonyme007]

Bonsoir à tous,
Sur le lien suivant : https://en.wikipedia.org/wiki/Navier...and_smoothness , on présente le système de Navier Stokes comme suit :

C'est un système hautement non linéaire, difficile à résoudre, non encore résolu actuellement dans son domaine approprié comme indiquée dans la page Wikipedia ci-dessus. Il présente l'un des problèmes du millénaire pour qui on offre 1 million de dollars pour le premier qui le résoudra par l'institut Clay of mathematics.
Ma question est la suivante,
Si on suppose que, , le système de Navier Stokes devient un système linéaire, comme suit :

Est ce que vous savez si les mathématiciens ont réussi à résoudre ce dernier système simplifié ci-dessus, qui est,
?
Merci d'avance.
-----

[gts2]

Bonjour,

Cela s'appelle le régime de Stockes, l'équation de Stokes, un écoulement rampant, et est valable à faible nombre de Reynolds.
Taper un des termes ci-dessus, vous allez trouver beaucoup de choses.

Remarque : on peut garder f sans problème s'il dérive d'un potentiel, et on peut ajouter pour simplifier \rho=constante, on peut alors grouper f et P dans un terme

[Opabinia]

Bonjour,

Les équations obtenues (II) sont bien linéaires, mais leurs solutions doivent vérifier les relations simplificatrices (I), et qui ne le sont pas:

[Opabinia]

Il faut multiplier par (ρ) l'équation initiale

et passer à la forme limite qu"elle prend lorsque (ρ) tend vers zéro: on obtient une équation approchée, dans laquelle intervient un nouveau coefficient de viscosité: µ = ρν .

https://fr.wikipedia.org/wiki/%C3%89..._Navier-Stokes

[A voir en vidéo sur Futura]

[albanxiii]

Bonjour,

Chapeau pour tout avoir écrit en LaTeX !

Il présente l'un des problèmes du millénaire pour qui on offre 1 million de dollars pour le premier qui le résoudra par l'institut Clay of mathematics..

Pas tout à fait, car on le résout numériquement. La page dit https://fr.wikipedia.org/wiki/Probl%..._Navier-Stokes :

Le prix récompense la démonstration de l'existence d'une solution régulière des équations pour un fluide incompressible.

[Anonyme007]

Bonjour,

Chapeau pour tout avoir écrit en LaTeX !

Oui, c'est un peu fastidieux.
Mais, pour raccourcir le chemin, je tape juste la première équation du système, ensuite, je fais copier/coller, parce que, les équations du système se ressemblent beaucoup. ça devient plus facile l’écriture en Latex comme ça.

Les équations obtenues (II) sont bien linéaires, mais leurs solutions doivent vérifier les relations simplificatrices (I), et qui ne le sont pas.

Oui, mais il est facile de montrer, grâce à la théorie des distributions, que les termes non linéaires du système s’annulent tous.

Cela s'appelle le régime de Stockes, l'équation de Stokes, un écoulement rampant, et est valable à faible nombre de Reynolds.
Taper un des termes ci-dessus, vous allez trouver beaucoup de choses.

Merci pour ces précisions gts2. C'est très instructif et édifiant ce que tu dis. Je vérifierai ces mots clés à tête reposé ce soir. Merci.

Cordialement.

[Anonyme007]

Bonsoir à tous,

Ce fil date de quelques semaines déjà. Je me permets de le déterrer à nouveau pour vous poser la question suivante,

Dans le problème du millénaire suivant, dit, de Navier Stokes : https://www.claymath.org/sites/defau...vierstokes.pdf , on demande de considérer les forces externes nulles si nous cherchons à montrer l'existence et la lissité des équations de Navier Stokes. Est ce qu'on peut les considérer non nulles si on veut montrer l'existence et la lissité des équations de Navier Stokes au lieu de nulles ?

Merci d'avance.