Question flotteur immergé

[peanjac]

Bonjour à tous,

Je me pose une question pour laquelle j'aurais besoin de vos éclaircissements.

Soit un flotteur de 1 m de long x 1 m de large x 0,1 m de hauteur plongé dans l'eau à 1 m de profondeur.

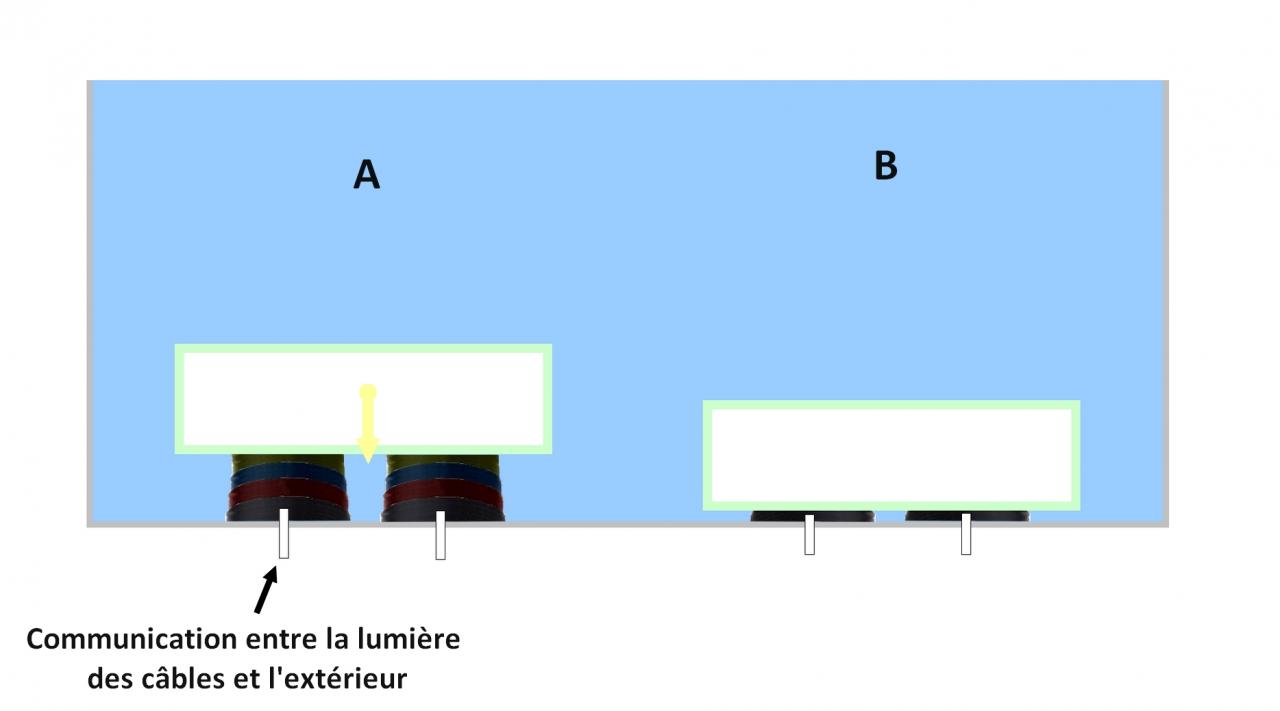
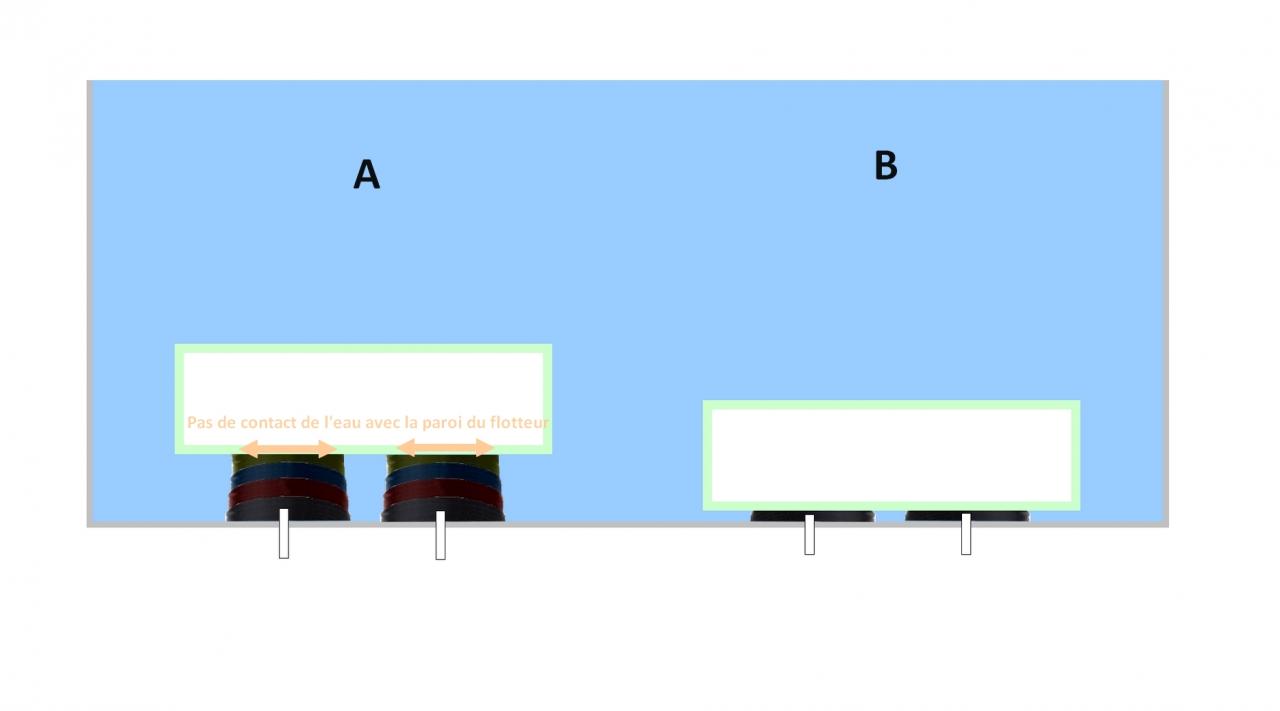
On applique sur la paroi inférieure de ce flotteur deux "câbles rétractables" qui fonctionnent comme représenté sur le deuxième schéma.
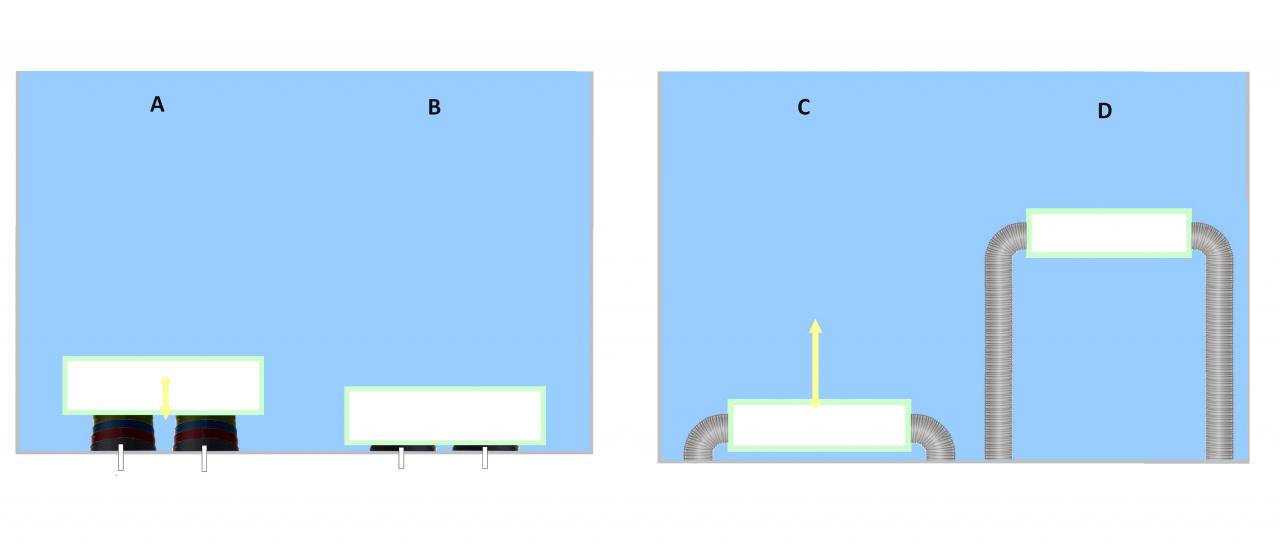
Ces câbles sont formés par une succession de maillons en forme de bague. Chaque maillon a un diamètre légèrement inférieur au maillon du dessous de sorte à ce que la bague jaune puisse descendre autour de la bleue, puis que les deux ensemble puissent descendre autour de la rouge, etc.
Le câble peut ainsi se déployer ou se rétracter à l'instar des antennes des anciens téléphones portables par exemple.

Au niveau des forces qui s'appliquent sur le flotteur j'ai noté F1 celle qui s'exerce sur la paroi supérieure du flotteur, F2 celle sur la paroi inférieure, F3 et F4 sur les paroi latérales. Il faudrait rajouter F5 et F6 pour celles s'exerçant sur les parois antérieure et postérieure non représentées sur cette vue 2D.



Ma question est la suivante; si les surfaces des câbles sont assez importantes, la flotteur peut-il descendre au fond de la cuve?

(Je néglige le poids du flotteur et la pression atmosphérique pour simplifier les choses).

Si on fait le calcul, il faudrait donc que F1 > F2 pour que le flotteur descende (F3, F4 et F5, F6 sont de valeur identique mais de sens opposé, elles s'annulent donc).

Ces forces sont égales à la pression P qui s'exerce sur les parois du flotteur multipliée par la surface S de ces mêmes parois, soit*: F1 = P1 x S1, F2 = P2 x S2.

P1 = ρ x g x h1 avec*:
- ρ la masse volumique du fluide
- g la constante de pesanteur
- h1 la hauteur d'eau.

Donc à 1 m de profondeur, P1 = 1000 x 9,81 x 1 = 10 000 N/m² (j'arrondis le 9,81 à 10 car plus simple pour les calculs).

Ainsi F1 = 10 000 N/m² x 1 m² = 10 000 N.

Pour que le flotteur descende il faut donc que*:
F1 > F2 soit P1 x S1 > P2 x S2, avec P1 = 10 000 N/m² et P2 à 1,1 de profondeur = 11 000 N/m².
Soit S2 < (P1 x S1) / P2
S2 < (10 000 x 1) / 11 000
S2 < 0,91 m².

Par conséquent, si la surface cumulée des 2 câbles est supérieure à 0,09 m², le flotteur pourrait-il descendre?


Merci pour vos réponses, désolé si j'ai fait des erreurs je ne suis pas très à l'aise en physique.


Base avec forces.jpg Maillon.jpg
-----

[XK150]

Salut ,

Une question en première lecture : Les " câbles " détendus ou rétractés sont toujours plein d'eau ??? Leur volume , masse sont constantes ? Comment sont ils commandés ?
Ce sont juste une série d'anneaux télescopiques non étanches ?

[peanjac]

Bonjour,

Les câbles peuvent effectivement être vus comme une série d'anneaux télescopiques étanches.
En position initiale avec le flotteur situé à 1 m de profondeur, les câbles sont détendus.
Pour chaque câble, une extrémité est fixée hermétiquement à la paroi inférieure du flotteur, la seconde au fond de la cuve.
La lumière des câbles est occupée par de l'air; ainsi pour ne pas mettre cette quantité d'air sous pression lors de la rétractation des câbles, il existe une communication sous la cuve entre la lumière des câbles et l'extérieur (représentée sur le premier schéma).

[XK150]

Re ,

Sans un schéma clair de l'ensemble , en position haute et basse , j'abandonne .

[A voir en vidéo sur Futura]

[Bounoume]

Pour que le flotteur descende il faut donc que*:
F1 > F2 soit P1 x S1 > P2 x S2, avec P1 = 10 000 N/m² et P2 à 1,1 de profondeur = 11 000 N/m².
Soit S2 < (P1 x S1) / P2
S2 < (10 000 x 1) / 11 000
S2 < 0,91 m².

Par conséquent, si la surface cumulée des 2 câbles est supérieure à 0,09 m², le flotteur pourrait-il descendre?

le raisonnement initial et les calculs me paraissent corrects....
faudrait simplement dire que S2, c'est la surface sur laquelle s'exerce la force dûe à la pression de l'eau (dirigée vers le haut) ET que cette surface, c'est la plaque de 1 m2, diminuée des zones trafiquées pour qu'aucune pression de l'eau ne s'y exerce.....
et ces zones sont les câbles bizarres.....

Ainsi
comme S2 + S_cables= 1 (en m2)
surface "câbles" = 1 -S2
d'où le résultat : faut que la surface totale des trous d'entrée des 'câbles' mesure (1 - 0,91) en m2 ......


remarque méchante: je mets au défi l'auteur du problème de réaliser ses fameux 'câbles' avec des coulissements étanches et sans forces de frottement.....
dans la vraie vie, ou bien ça va fuir de partout, ou bien pour diminuer les fuites il faudra bien ajuster les cercles et alors tenir compte de forces de frottement. entre anneaux.... ...

D' autres avis plus compétents?
A +

[peanjac]

Bonjour XK150,

Désolé si les explications n'étaient pas claires, je joins le schéma d'ensemble suivant (j'ai raccourci la taille des câbles pour gagner du temps à sa réalisation).

En situation A le flotteur est en position haute à 1 m de profondeur, les câbles sont détendus.
Le flotteur va descendre sous l'effet de F1 > F2 comme expliqué ci-dessus, pour se retrouver en position basse (situation B).
En situation B les câbles sont rétractés avec les maillons les un à l'intérieur des autres (comme illustré sur le précédent schéma).

[XK150]

Si les anneaux télescopiques ne présentent aucun frottement , ni autre résistance ( puisqu'ils sont à P atm .) , ils ne jouent aucun rôle entre les situations A et B .

Si , en A , le flotteur est tel qu'il coule , il coule jusqu'en B .
Si , en A , le flotteur est entre 2 eaux , il reste à sa position .
Si , en A , le flotteur a envie de remonter , il remonte en entraînant les anneaux téléscopiques .

Je ne vois pas ce qui vous pose problème , il n'y a besoin d'aucun calcul . A vous pour m'expliquer ce qui m'échappe ...

[XK150]

Maintenant ,si l'on veut tenir compte de la force -poids des anneaux et de leur poussée d'Archimède , les 3 mêmes cas sont aussi possibles :

- Le flotteur se stabiise entre 2 eaux , certains anneaux posés sur le fond ( dessin A )
- Le flotteur coule simplement avec le poids du dernier anneau , tous les anneaux posés sur le fond ( dessin B )
- le flotteur entraîne tous les anneaux vers le haut .

[peanjac]

Bonjour,

Les anneaux télescopiques permettent de diminuer la surface S2 de la paroi inférieure du flotteur où s'exerce la force due à la pression de l'eau, comme l'a noté Bounoume.
En effet, les anneaux sont hermétiques et étanches, ainsi la pression hydrostatique ne s'exerce pas sur toute la surface de la paroi inférieure du flotteur mais uniquement sur S2 = Surface paroi inférieure - Surface câble.

Le rôle des câbles (= anneaux télescopiques) est de diminuer suffisamment S2 pour que F1 > F2 et que le flotteur descende.

[XK150]

Re ,

Oui , mais à partir de la situation d'équilibre A , par exemple , le flotteur ne descendra jamais tout seul ?? La situation est figée sans action extérieure .

[peanjac]

Bonjour,

La situation A n'est pas à l'équilibre, F1 étant supérieur à F2, le flotteur va avoir tendance à descendre et à gagner le fond de la cuve d'eau comme représenté en B.

Meilleurs vœux au passage!

[non bwana]

Bonjour,

Au niveau des forces qui s'appliquent sur le flotteur j'ai noté F1 celle qui s'exerce sur la paroi supérieure du flotteur, F2 celle sur la paroi inférieure, F3 et F4 sur les paroi latérales.

Il faudrait rajouter F5 et F6 pour celles s'exerçant sur les parois antérieure et postérieure non représentées sur cette vue 2D.

Il faudrait tenir compte de la poussée d’Archimède, qui correspond à l’opposé du poids du fluide déplacé. Et le poids du fluide déplacé est directement lié au volume de votre flotteur. La poussée d'Archimède est verticale et dirigée vers le haut.
Que votre flotteur soit posé plutôt à plat, ou plutôt debout ne change rien à la poussée d'Archimède, (penser aux bouchons de pêche, de formes bien variées n'influençant pas la flottabilité). Dans votre montage, votre flotteur ayant une densité inférieure à celle de l'eau va remonter. Avec ou sans queue articulée, son volume ne change pas, et si sa queue est remplie d'air, on peut considérer l'ensemble comme un seul élément, et ça va remonter plus vite encore, l'augmentation globale du volume va amplifier la poussée d'Archimède.

[XK150]

Bonjour,

La situation A n'est pas à l'équilibre, F1 étant supérieur à F2, le flotteur va avoir tendance à descendre et à gagner le fond de la cuve d'eau comme représenté en B.

Meilleurs vœux au passage!

Bonne année !

Oui , je l'ai écrit au post 7 , premier cas , donc nous sommes d'accord . Ce n'est pas un flotteur : il n'a jamais flotté depuis le début de son immersion ! Après ???

[peanjac]

Bonjour!

Désolé pour le délai de réponse!

Effectivement nous sommes d'accord, le flotteur n'a jamais flotté depuis le début de son immersion, il descend au fond de la cuve et passe de la situation A à la situation B.
Pour rappel, sa descente est liée au fait que F1 > F2 car S2 est suffisamment inférieur à S1 grâce à l'effet des câbles.

Mon interrogation est la suivante; une fois que le flotteur est au fond de la cuve, si on place les câbles non plus sur la paroi inférieure mais sur deux parois latérales (situation B -> C), est-ce que le flotteur pourrait remonter?

En effet en plaçant les câbles sur les parois latérales on libère de la place sur S2 qui devient égale à 1 m², ainsi F2 > F1 et donc le flotteur serait amené à monter? (situation C -> D)
Les deux câbles ayant le même diamètre, ils amputent les deux faces latérales de la même surface et donc la pression hydrostatique qui s'exerce sur les parois latérales, F3 et F4, restent de valeur identique et de sens opposé, ainsi elles s'annulent toujours.

Le flotteur pourrait-il dans cette configuration remonter? Dans le même temps les câbles pourraient-ils se déplier pour revenir comme en position A?

Je joins le schéma d'ensemble pour plus de clarté (j'ai changé l'aspect des anneaux télescopiques de B en C parce que c'était plus simple à représenter).

[XK150]

Re ,

Sur la nouvelle figure , vous avez oublié les évents au fond des soufflets ( important , les évents ). Et disons " soufflets " et non pas " câbles " .

Comme le premier : s'il est descendu tout seul , lentement ( pour éviter de parler inertie ) , il ne remontera pas : en position basse , il est au mini de la poussée d' Archimède sur le volume total .
La poussée d' Archimède ne va pas augmenter miraculeusement en position basse , sans aucune intervention externe .

[XK150]

Si vous cherchez à obtenir un mouvement oscillant , alternatif gratuit et perpétuel , ce n'est pas utile d'insister : ce n'est pas possible .

[peanjac]

Bonjour,

Merci pour votre réponse.
On est bien d'accord, aucune faisabilité du perpétuel, pas de débat là-dessus.
Effectivement je n'avais pas représenté les évents sur le dernier schéma pour simplifier, mais ils sont bien là!

La poussée d' Archimède ne va pas augmenter miraculeusement en position basse , sans aucune intervention externe .

Pour moi en situation C, le fait que les soufflets se déplacent de la paroi inférieure aux parois latérales permettrait que la résultante des forces soit dirigée vers le haut et que le flotteur remonte.

Je crois que c'est ma compréhension de la poussée d'Archimède (PA) qui est peut-être mauvaise, et j'aimerais comprendre pourquoi.
Pour moi, la PA correspond à la résultante des forces issues des pressions hydrostatiques qui s'exercent sur les parois d'un objet totalement ou partiellement immergé. Dans la majorité des cas, on peut l'estimer par l’opposé du poids du fluide déplacé comme le disait non bwana au message 12. Mais dans la situation A où l'ensemble de la paroi inférieure de l'objet n'est pas au contact de l'eau et donc pas soumise à la pression hydrostatique (la paroi inférieure du flotteur n'est pas au contact de l'eau au niveau de la lumière des soufflets, cf image infra), le calcul est un peu différent.

Ainsi, si on reprend les calculs.

Situation A :

Comme décrit dans le message 1, le flotteur qui mesure 1 m de long x 1 m de large x 0,1 m de hauteur est plongé à une profondeur de 1 m d'eau. Les soufflets sont bien appliqués à sa paroi inférieure.
La résultante des forces = F1 (force qui s'exerce sur la paroi supérieure) + F2 (force sur la paroi inférieure) + F3 + F4 + F5 + F6 (forces sur les parois latérales).

A) Sans les soufflets on aurait :
• F1 = P1 x S1 avec P1 la pression qui s'exerce sur la paroi supérieure et S1 la surface de la paroi supérieure
P1 = ρ x g x h1= 1000 x 9,81 x 1 = 10 000 N/m² (j'arrondis le 9,81 à 10 car plus simple pour les calculs).
S1 = 1 m²
Donc F1 = 10 000 x 1 = 10 000 N.

• F2 = P2 x S2
P2 = 1000 x 10 x 1,1 m = 11 000 N/m²
S2 = 1 m²
F2 = 11 000 N.

• F3, F4 et F5, F6 sont de valeur identique mais de sens opposé, elles s'annulent donc.

La résultante des forces est alors F1 + F2 soit F1 - F2 car F2 est de sens opposé à F1, soit 1 000 N dirigée vers le haut, donc le flotteur remonte. Ces 1 000 N correspondent à l'opposé du poids du fluide déplacé, la configuration classique, on retombe bien sur l'estimation habituelle de la PA.

B) Avec les soufflets :
• F1 est toujours égale à 10 000 N.

• Pas de changement pour F3, F4 et F5, F6 qui s'annulent toujours.

• En revanche F2 = P2 x S2
P2 = 11 000 N/m²
S2 = surface de la paroi inférieure - surface des soufflets = 1 m² - 0,1 m² = 0,9 m²
Donc F2 = 11 000 x 0,9 = 9 900 N.

La résultante des forces est toujours F1 + F2 soit F1 - F2, soit dans ce cas 100 N dirigée vers le bas donc le flotteur descend.



Situation C :

Le flotteur est maintenant au fond de la cuve à 1,5 m de profondeur. Les soufflets sont passés sur 2 de ses parois latérales.

La résultante des forces est :
• F1 = P1 x S1
P1 = 1000 x 10 x 1,5 = 15 000 N/m²
S1 = 1 m²
F1 = 15 000 N.

• F2 = P2 x S2
P2 = 16 000 N/m²
S2 n'est alors plus diminuée par la surface des soufflets et devient égale à 1 m²
F2 = 16 000 N.

De plus comme dit dans le message 14, les deux soufflets ayant le même diamètre, ils amputent les deux faces latérales de la même surface et donc la pression hydrostatique qui s'exerce sur les parois latérales, F3 et F4, restent de valeur identique et de sens opposé, ainsi elles s'annulent toujours.
F5 et F6 ne sont pas modifiées.

Donc la résultante des forces reste F1 + F2 soit F1 - F2 et devient égale à 1 000 N dirigée dans le sens de F2, soit vers le haut. Le flotteur remonte.

En substance, le rôle des soufflets est de diminuer la surface de la paroi inférieure en contact avec l'eau, afin de diminuer F2 pour permettre au flotteur de descendre.
Puis en se plaçant sur les parois latérales, permettre au flotteur de remonter au sein de la cuve.

[XK150]

Pas besoin de faire aucun calcul : il suffit de raisonner en poussée d'Archimède .
ou de se dire : " s'il est descendu tout seul au fond , il ne remontera pas " .
S'il remontait , pourquoi attendre d'être arrivé au fond ? S'il devait remonter , pourquoi descendrait il ???

Mais si un participant veut s'attaquer à votre raisonnement , libre à lui .

[XK150]

En fait , je suis allé un peu vite face au tout derner dessin , mais cela reste vrai :

Dans ce dernier dessin , dans les 2 cas la poussée d'Archimède est la même dans les 2 cas , puisque , dans les 2 cas , la surface du flotteur sous les soufflets est occultée de la même valeur .
Les surfaces sont occultées , il n'y a pas de poussée résultante pour ces surfaces .
Donc , au point de vue poussée A = B .
Si le flotteur est descendu , c'est que la force poids ( la même dans les 2 cas ) est supérieure à la poussée d' Archimède ( la même dans les 2 cas ) .

Montrez moi ce qui diffère en terme de poussée puisque nous sommes d'accord de dire que le poids ne varie pas .

[XK150]

Vos objets , appelés flotteurs , n'ont jamais flotté : ce sont des objets , qui abandonné près de la surface ; coulent ( lentement ) .
Pour l'instant , on considère les soufflets petits , fins , sans masse , étanches juste au contact des boîtes : pour l'instant , on néglige tout effet de leur part .

Dans ces conditions , pour que la boîte remonte arrivée au fond ( ou au cours de la descente ) , il n'y a que 2 possibilités :
- elle perd du poids , donc de la masse au cours de la descente ou au fond ( par exemple , une enveloppe externe qui se dégraderait peu à peu au contact de l'eau ).
- arrivée au fond , elle augmente de volume et de surface ( cette application existe avec des ballons vides immergés puis gonflés qui remontent des charges immergées ) .
Dans ce cas , on va devoir fournir de l'énergie pour gonfler la boîte .

A ces 2 possibilités , s'ajoute une condition : la surface des boîtes est toujours entièrement mouillée , pour éviter tout problème de raisonnement avec le contact sur le fond .
On suppose donc le repos sur le fond , sur quelques contacts ponctuels .

Une fois ceci admis , on examinera le rôle des soufflets selon leur montage . Déjà , on peut dire que ça n'arrange rien , au contraire .

[peanjac]

Bonjour,

Merci pour les réponses!
On est d'accord pour dire que la poussée dans la situation A est la même qu'en B, c'est juste le flotteur qui est descendu.

s'il est descendu tout seul au fond , il ne remontera pas

Le flotteur descend parce que la force qui s'applique sur la paroi supérieure du flotteur est supérieure à celle qui s'applique sur la paroi inférieure; et ce grâce au rôle des soufflets qui diminuent la surface de la paroi inférieure du flotteur sur laquelle s'applique la pression hydrostatique (cf message 17).
Ensuite, une fois que le flotteur est au fond de la cuve, il va pouvoir remonter car les soufflets se déplacent de la paroi inférieure aux parois latérales et ainsi la pression hydrostatique de l'eau va s'appliquer sur l'ensemble de la paroi inférieure. Ce faisant, la force qui s'applique sur la paroi inférieure devient supérieure à celle qui s'applique sur la paroi supérieure du flotteur, donc il remonte.

C'est cela qui diffère en terme de poussée, la surface de la paroi inférieure sur laquelle s'applique la pression hydrostatique n'est pas la même entre les situations A/B et C/D, et donc la poussée qui en résulte diffère.

C'est la 3ème possibilité qui s'ajoute aux 2 autres que vous évoquez au message 20, avec lesquelles je suis parfaitement d'accord!

[XK150]

Car maintenant les soufflets se déplacent tout seul d'une paroi à une autre ?? Je n'ai encore pas vu ce dessin .

Donc , le système descend , puis remonte , puis descend , puis remonte ????

[ArchoZaure]

Bonjour.

Vous devriez commencer par simplifier le schéma.
Inutile de mettre deux câbles, circulaires en plus
Un seul "câble télescopique" rectangulaire de la forme du flotteur fera très bien l'affaire.

Concernant le fond de l'affaire.

Ces forces sont égales à la pression P qui s'exerce sur les parois du flotteur multipliée par la surface S de ces mêmes parois, soit*: F1 = P1 x S1, F2 = P2 x S2.

Il me semble que ceci est faux.

La force d'Archimède qui s'applique à une objet immergé dans un liquide ne dépend pas de sa forme mais de son volume.
Puisque si c'était vrai (pression*surface) ça voudrait dire que selon le rapport surface/volume on n'aurait pas la même force.
La sphère ayant le meilleur rapport surface/volume, elle flotterait mieux qu'un cube :
https://fr.wikipedia.org/wiki/Rapport_aire-volume

[gts2]

Concernant le fond de l'affaire
"Ces forces sont égales à la pression P qui s'exerce sur les parois du flotteur multipliée par la surface S de ces mêmes parois, soit : F1 = P1 x S1, F2 = P2 x S2"
Il me semble que ceci est faux.

C'est juste dans la situation indiquée : parallélépipède horizontal.

Mais je n'ai toujours pas compris comment cela fonctionne, le but du jeu ...

[peanjac]

Bonjour,

Merci à tous pour vos réponses!

Car maintenant les soufflets se déplacent tout seul d'une paroi à une autre ?? Je n'ai encore pas vu ce dessin .

Oui c'est ce que j'évoquais dans les messages 14 et 17 (paragraphe sur la situation C).
Une fois que le flotteur est au fond le cuve, les soufflets passent de la paroi inférieure aux parois latérales. Sur les schémas, c'est le passage de la situation B à la situation C (cf message 14).

Inutile de mettre deux câbles

L'idée de mettre deux câbles est pour ne pas créer de déséquilibre lorsque le flotteur remonte avec chaque câble fixé sur une des parois latérales.

Il me semble que ceci est faux.

Comme le confirme gts2, dans le cas où le flotteur est un parallélépipède horizontal, je pense que les forces qui s'exercent sur les parois du flotteur sont bien égales à F = Pression x Surface.
Pour rester sur Wikipédia que vous citez, sur la page de la poussée d'Archimède au paragraphe "Idée de la démonstration", ils expriment bien la force qui s'exerce sur la paroi du cube comme le produit de la pression de l'eau et de la surface du cube -> https://fr.wikipedia.org/wiki/Pouss%...Archim%C3%A8de.

Mais je n'ai toujours pas compris comment cela fonctionne, le but du jeu

Comment puis-je vous aiguiller? Vous pouvez jeter un œil au schéma d'ensemble qui est montré au message 14.
Est-ce que pour vous la démonstration du message 17 est correcte?