Bonjour à tous,
Le modele d'Hodgkin et Huxley modélise le comportement électrique d'un neurone à partir de raisonnement mathématique et physique sur l'electricité, et de données expérimentales. Je ne vais pas en refaire la démonstration, ça serait un peu long ^^
J'essaie d’implémenter ce modele avec python, mais je n'y arrive pas.
Voilà mon code :
Cliquez pour afficher
Dans ces conditions, le potentiel, stocké dans V, doit etre égal à 0 (conditions de repos). Or le plot qui sort est égal à zéro pendant un petit moment, puis il plong tout d'un coup. Quand je print V, la valeur augmente petit à petit, de maniere infinitesimale, puis d'emballe, devient inf, puis nan nan nan .... Quand je print le temps, tps, alors qu'il devrait etre égal à 0 ; 0,01 : 0,02 ; 0,03..., il n'est pas régulier et ressemble plutot à 0 ; 0.01 ; 0.0199999999999, 0.0300000002. Je me pose donc en premier lieu la question suivante : pourquoi le temps n'est il pas régulier ?
Il y a ensuite beaucoup de questions à poser sur le fonctionnement de mon code, mais il faudrait rentrer dans les détails pour en parler, ce que je ne compte pas faire si personne n'est intéressé pour m'aider ^^
-----






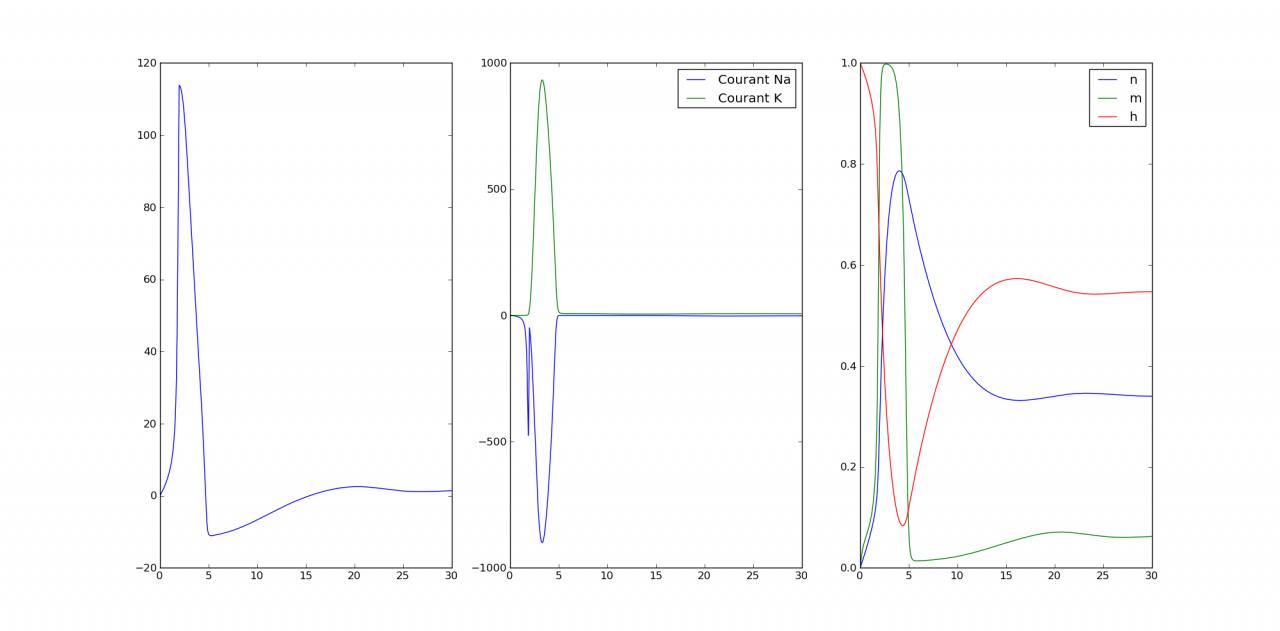
 : le PA est aussi beau qu'un vrai ! Voire plus
: le PA est aussi beau qu'un vrai ! Voire plus 