Somme vectorielle

[geometrodynamics_of_QFT]

Bonjour,


Je souhaite effectuer une somme de vecteurs

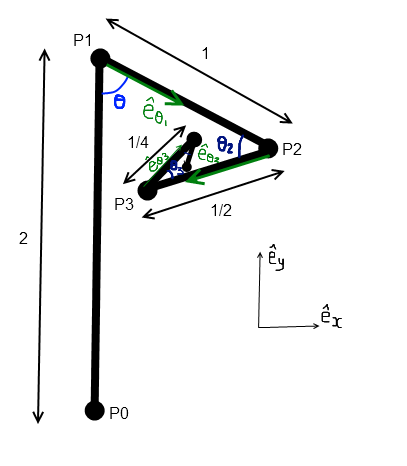
Chacun des vecteurs a une taille et une orientation différente, dépendant toutes d'un unique paramètre .

Soit

où

• est un paramètre réel dans l'intervalle .
• est un vecteur unité donné par la formule de récurence : avec et
• est perpendiculaire à et défini par ( = vecteur plongeant dans le plan)
• et par récurence pour n>1 :

Question : Formuler en termes de composantes en et , et /ou trouver l'expression paramétrique (paramètre = ) du point de convergence.

Toutes les informations sont-elles présentes pour résoudre le problème?
Je ne vois pas du tout comment résoudre cette équation de récursion vectorielle...
Aussi, vaut-il mieux calculer une somme finie pour N termes, et ensuite prendre la limite pour N tend vers l'infini, ou bien calculer directement la somme pour une infinité de termes?
Je vous remercie infiniment pour votre aide!
-----

[geometrodynamics_of_QFT]

J'ai avancé sur quelques points :

• partant de l'expression corrigée par rapport au post précédent :
  ,
  et de la déduction
  
  
  Je cherche à exprimer et en terme de uniquement, et de et
  
• De la relation de récurence pour :
  pour n>1 : ,
  On déduit:
  
  donc :
  
  
  Mais comme , on réexprime comme :
  .
  
• Partant de cette dernière expression, on l'insère dans la formule de récurence pour et :
  
  ,
  et
  
  
  Utilisant et , on tire:
  
  et
  
  
  On réécrit donc la relation de récurence comme:
  ,
  et
  
  où
  
  
  et
  
  
• à partir de ce moment, je bloque. Car si on applique la récurence une fois par exemple:
  
  
  
  
  
  Une idée pour généraliser de la même manière que pour les angles? Je perçois un binôme de newton (a-b)^n...mais vu que les termes sont vectoriels...comment les distinguer dans le développement de Newton?
  
  Je vous remercie!
  

[geometrodynamics_of_QFT]

Deux derniers points :

• Au cas où ce n'était pas clair, tout se passe dans le PLAN. C'est donc une somme vectorielle de vecteurs qui sont tous dans le même plan (x,y).
• On peut écrire la relation de récurence pour les vecteurs unitaires sous forme matricielle :
  
  
  
  Appelant la matrice ,
  
  On peut écrire:
  
  
  Et comme , que et que ,
  
  On réécrit :
  
  
  

Est-ce qu'une âme charitable pourrait vérifier ces calculs ou le raisonnement?
comment effectuer le produit des matrices M? C'est précisément ça qui me bloque...
De plus, ici, il semble ne pas y avoir moyen de ne pas passer par une somme finie (N)...Cela est-il normal? Peut-on réexprimer M autrement pour que le produit ne fasse pas intervenir N explicitement?

[geometrodynamics_of_QFT]

un feed-back serait hautement apprécié...

Je réponds à toute question concernant des points qui vous paraissent obscurs dans le raisonnement!

[A voir en vidéo sur Futura]

[geometrodynamics_of_QFT]

Voici une illustration du problème considéré:

[LPFR]

Bonjour.
Ce problème me rappelle la spirale de Cornu.
Je n’ai pas l’impression qu’il soit soluble analytiquement.
Au revoir.

[geometrodynamics_of_QFT]

Bonjour LPFR,

ce n'est pas une spirale, car les points (coudes) reliant les arcs de cercles n'ont pas une dérivée continue...et encore moins si on ne regarde que les segments [POP1], [P1P2], etc...

Je me rends compte que la principale difficulté vient du fait que chaque angle est défini récursivement par rapport au précédent , ce qui rend l'expression des composantes de son vecteur unitaire associé difficile dans le repère (x,y) (sauf pour évidemment). Mais il doit bien exister des méthodes oud es "trucs" pour procéder à ce type d'addition vectorielle non?
Des idées pour procéder?

Je vous remercie beaucoup!!!

[geometrodynamics_of_QFT]

spirale de cornu (wikipedia)

ou encore plus récemment spirale de transition d'un rail de Talbot (suite aux travaux cherchant à réduire les effets d'une montée brutale de la force centrifuge dans l'amorce d'un virage), une dénomination qui recouvre aussi son utilisation dans la conception des raccordements de virages routiers.

excellent je ne voyagerai plus jamais de la même façon en voiture
(même si je ne voyage pas en voiture. (et je conseille à tout le monde d'en faire autant))

Bref :
Après avoir regardé un peu plus en détail l'article, je suis maintenant certain que ce sont deux situations tout à fait différentes. De par leur construction d'une part, et de par leurs expressions d'autre part.

j'ai réalisé un album imgur qui reprend les étapes parcourues pour arriver jusqu'ici.
mais tout vient d'ici (je veux dire, de ce forum):

Je reprends mon message #65 du fil "lieu inhabité" pour pouvoir parcourir tout aussi rapidement les étapes, et je reposte une image de l'origine de cette construction.

La poursuite de l'aventure se déroule désormais sur ce fil, où l'on essaie de localiser le point de convergence des arcs de cercles orange.

Mais je suis disponible sur ce fil-ci pour toute remarque, suggestion, correction, vérification, etc...relatives aux calculs pour obtenir F(x), qui était l'objet de ce fil-ci. Le réumé des calculs est disponible sur ce fil.
Je souhaite réellement obtenir des confirmations des résultats, car sinon les erreurs se propagent dans la suite du raisonnement.
Par exemple, pour la formule de récurence pour dans l'épisode suivant....

Pour rappel, nous étions partis d'un simple problème, pour en arriver jusqu'ici!

A bientôt dans la jungle mathématique!

ster5.png


LPFR, je compte sur votre intuition géniale et votre expertise mathématique pour me donner une feed-back de cette équation dans mon post #3 de ce fil (tout le raisonnement y est depuis le post #1):


Est-elle correcte? Comment la résoudre?
Je vous remercie d'avance!
de l'aide s'il vous plait!

[geometrodynamics_of_QFT]

Ici, la FORME et le POINT de convergence CHANGENT en fonction de l'unique paramètre !

Les conditions limites permettent de prédire que le point de convergence est en ( 0 , -1+(2-1+1/2-1/4+1/8-1/16-...) = 1/3? pour (tous les segments alignés sur l'axe [POP1] = axe y), et tend vers (1-1/2+1/4-1/8+1/16-... , 1 ) pour

[geometrodynamics_of_QFT]

Cela découle de pour , et , si toutefois cette relation obtenue précédemment est correcte!!?? L'est-elle????

edit :

et tend vers (1-1/2+1/4-1/8+1/16-... , 1 ) pour

évidemment, et pas lol.

[geometrodynamics_of_QFT]

edit-edit:

et tend vers (1-1/2+1/4-1/8+1/16-... , 1 ) pour

C'est faux
On ne connait pas ce point de convergence pour : tous les angles sont "droits"...(avec des pincettes)

Désolé, pour les lecteurs fantômes ...donc on ne connait QUE le point initial de mon post #9.

[azizovsky]

Salut, je laisse la rigueur mathématique au spécialiste ...., ma vision de ce que tu propose est la suivante :

tu fait une sorte de série de Fourier à une vecteur, et ton concept ne s'applique que spineurs, je m'explique :

, on pose :

ce qui donne :




avec la condition :

pour avoir à la fin :



je n'est rien dit .

[azizovsky]

ton concept ne s'applique que spineurs

je voulais dire qu'a une sorte de 'spineur'.

[geometrodynamics_of_QFT]

Ce n'est pas du tout une série de Fourier..même si ça y ressemble mathématiquement peut--être...

et si tu veux une opération en terme de "spineurs", tu n'as qu'à écrire ceci mais de manière correcte ( :-s j'arrive pas) pendant que je réfléchis à ce que tu as voulu dire:



Do you see what i mean?

mais je crois qu'il faut sortir la somme du premier vecteur...car ça marche pas sinon.
Donc :

[geometrodynamics_of_QFT]

pour que ça marche avec n=1, j'ai qu'à croiser les doigts...

dernière update (petit détail):


Donc le membre de droite ne contient que des termes en theta et n...maintenant il faut calculer...et j'suis bloqué!

[azizovsky]

je t'ai proposé un modèle mathématique pour ton concept que je n'arrive pas à cerner ...(pas de concentration pour l'instant...), s'il ne convient pas à ton idée, la poubelle.....

[geometrodynamics_of_QFT]

je t'ai proposé un modèle mathématique pour ton concept que je n'arrive pas à cerner ...(pas de concentration pour l'instant...), s'il ne convient pas à ton idée, la poubelle.....

Mais ce modèle mathématique ne convient pas à la situation, c'est la difinition d'une décomposition d'une fonction d'onde en série de Fourier, ou un truc du style...je ne crois pas que nous soyons dans un espace de Hilbert ici...on fait de la géométrie euclidienne...

regarde mon dessin du post #5:
chaque vecteur fait un angle par rapport au vecteur précédent , et pas par rapport aux axes et . D'où la formule de récurence.
C'est limpide et trivial...

[geometrodynamics_of_QFT]

Seule la direction de est définie par rapport à et ...(ainsi que pour son compagnon perpendiculaire)

...(ainsi que pour son compagnon perpendiculaire)

(réfère-toi au dessin)

[azizovsky]

j'ai représenté ton vecteur par .
en tous les cas, bon courage.

[geometrodynamics_of_QFT]

C'est à ça que j'aimerais arriver :
http://tube.geogebra.org/m/2786527 (faire bouger le point A1)

Ok, je vois où tu veux en venir...
Mais que faire avec les sinon les sommer comme je fais? Comment trouver les poids et ?

[geometrodynamics_of_QFT]

j'ai du mal avec ton concept...tu pourrais expliquer un peu plus en détail? pourquoi tu imposes cette condition? que représente-t-elle?

Et aussi, prends le dessin du post #5, prend un bonne taffe, et relis, CALMEMENT et en comprenant CHAQUE petit BOUT de caractère, les posts #1, #2 et #3.

Et demande moi clairement ce que tu ne comprends pas précisement.

[azizovsky]

un simple exemple: dans le plan : on représente un vecteur par un nombre complexe: et comme base,si comme tu 'as fais une projection d'un cercle orthogonal au plan, si le point représenter par z tourne dans l'espace, donc il décrit un cercle dans l'espace, on peut la représenté par : le couple: comme les coordonnées dans cette base de l'espace (exactement de la sphère avec la condition d'orthogonalité des vecteurs

[azizovsky]

le couple: comme coordonnées, on peut décrire n'importe quel cercle sur cette sphère en variant un seul paramètre de la représentation.

[azizovsky]

on peut décrire n'importe quel cercle sur cette sphère en variant un seul paramètre de la représentation.

annulé, j'ai fait 'rfissa'(huile d'olive+harcha(sorte de pain) +mélangé )...

[geometrodynamics_of_QFT]

Ok merci donc je vois un peu, même si c'est de la nouvelle matière pour moi...

Une sorte d'autre façon d'écrire des cercles en quelque sorte...
Mais comment cela peut-il aider ici? Car il n'y a plus de cercles dans ce problème, que des angles donnés par récursion, et des directions dépendant des angles...
Où vient s'implanter mathématiquement ta représentation dans ce shéma?
Merci a+

[azizovsky]

Ok merci donc je vois un peu, même si c'est de la nouvelle matière pour moi...

Une sorte d'autre façon d'écrire des cercles en quelque sorte...
Mais comment cela peut-il aider ici? Car il n'y a plus de cercles dans ce problème, que des angles donnés par récursion, et des directions elles aussi données par récursion...
Où vient s'implanter ta représentation dans ce shéma?
Merci a+

ok, laissé moi le temps de digérer ton idée, merci.

ps: regarde les spineurs comme ici http://www.math.unicaen.fr/lmno/sema...re/spinors.pdf

il y'a le livre d'Elie Carton : the theory of spinors.

[azizovsky]

on représente un point sur la sphère par deux variables seulement.

[geometrodynamics_of_QFT]

on représente un point sur la sphère par deux variables seulement.

Oui, car c'est une surface à deux dimensions (rayon fixe, deux angles)
Je vois l'idée des spinors, j'ai eu des cours de QED...mais je ne vois pas comment ils pourraient intervenir ici...
Pour rappel, tout se passe dans le plan...Pourquoi serait-il profitable d'introduire la notation complexe ici?

edit : Quoique...

Mais on additionne des exponentielles ici, on ne les multiplie pas...donc pas d'addition d'angles?

[geometrodynamics_of_QFT]

Pfff..ça m'énerve y'a à chaque fois une nouvelle faute :
Pour la nème fois:



cette fois--ci j'espère que c'est juste!

[azizovsky]

ok, dans ce cas, je ne vois pas mieux que le diagramme de Fresnel pour n vecteur :comme ici (3 vecteurs):https://www.google.be/search?q=diagr...HS5RCqIQsAQIGg

Bonjour,


Je souhaite effectuer une somme de vecteurs

Chacun des vecteurs a une taille et une orientation différente, dépendant toutes d'un unique paramètre .