Opération sur les incertitudes

[invitebb1eae45]

Bonjour ,

j'ai cette formule j'aimerais savoir comment faire pour avoir incertitude sur L merci beaucoups
L= √((D²/4)+(Di+e))

merci beaucoup
-----

[gg0]

Bonjour.



Je te laisse finir. J'ai utilisé l'incertitude relative pour éviter de compliquer avec la racine carrée (mais elle reviendra quand on multipliera par L), puis les formules de base des incertitudes.

Cordialement.

NB : On peut aussi utiliser des dérivées partielles, si on tient vraiment à faire des calculs compliqués.

[invitebb1eae45]

merci qu es ce qui reviendra de quoi parles tu?

[gg0]

Fais le calcul, puis tu comprendras.

A priori, en français, "elle" réfère toujours au nom apparu immédiatement avant.

[A voir en vidéo sur Futura]

[invitebb1eae45]

moi je me retrouve avec ce calcul 1/2 (D/2*Delta_D+Delta_Di +Delta_e)(1/4D²+Di+e)



je vois pas comment retrouve la fameuse racine

merci

[invitebb1eae45]

[QUOTE=gg0;5636165]Bonjour.

[invitebb1eae45]

∆L=L/2*(D/2*∆D+∆∅int+∆e)/(1/4 D²+∅int+e)

[Dlzlogic]

Bonjour,
Au risque de me répéter, je vous conseille de prendre les choses par le bon bout.
Vous avez une formule qui calcule une valeur numérique à partir de différents éléments, normalement des mesures élémentaire.
Chaque mesure élémentaire est entachée d'une erreur accidentelle, l'imprécision.
Cette valeur d'imprécision est connue, c'est marqué sur le mode d'emploi de l'appareil. Elle porte le nom d'erreur moyenne quadratique ou d'écart-type.
Le but de l'opération est de calculer l'imprécision de la combinaison de tous ces éléments c'est à dire l'imprécision sur le résultat définitif.
Avant de vous embarquer dans des calculs, vous devriez résoudre des choses simples,
Dans votre cours, qu'est-il dit sur la composition des erreurs accidentelles ?

[gg0]

Bon,

si tu tiens à écrire n'importe quoi, pas la peine que je prenne du temps pour toi.

Mais en réécrivant sérieusement le message #7 et en remplaçant L par sa valeur, on fait le calcul ...

NB : Tu peux écrire en LaTeX sur le forum, pour avoir (après prévisualisation, pour rectifier les erreurs) un texte bien écrit. Si vraiment tu n'y connais rien en LaTeX, un scan d'un texte bien écrit (après avoir été bien réfléchi) est aussi lisible (mais tardivement à cause des validations).

[invitebb1eae45]

Bon,

si tu tiens à écrire n'importe quoi, pas la peine que je prenne du temps pour toi.

Mais en réécrivant sérieusement le message #7 et en remplaçant L par sa valeur, on fait le calcul ...

NB : Tu peux écrire en LaTeX sur le forum, pour avoir (après prévisualisation, pour rectifier les erreurs) un texte bien écrit. Si vraiment tu n'y connais rien en LaTeX, un scan d'un texte bien écrit (après avoir été bien réfléchi) est aussi lisible (mais tardivement à cause des validations).

voila en un peu plus compréhensible encore desolé le LaTEX est un peu complexe on s'emmele vitte les pinceaux
je ne vois pas comment faire apparaître ma racine dans cette formule ou alors quelque chose m'echappe

[invitebb1eae45]

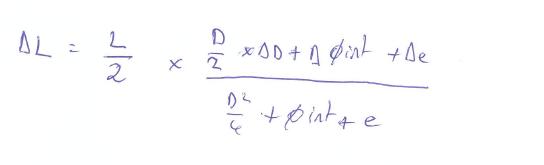
j'ai un resultat de +/- 0.06 mm pour D=431 mm , Di =88.9 mm , L=233.73 mm, e=1.6mm

[gg0]

1) Si tu changes tes notations en cours de route sans le dire, tu n'es plus crédible
2) La racine carrée est dans le L. Comme tu utilises la valeur calculée, tu l'utilises bien, mais tu la caches. J'avais supposé que tu voulais une formule en fonction seulement de D, Di et e.

[Dlzlogic]

Bonsoir,
Il y a un point qui me chiffonne, la formule de L n'est pas homogène. C'est une erreur de copie ou un exercice totalement artificiel ?
Si vous donnez une bonne formule, je peux, avec l'accord de la modération, vous donner la méthode de calcul.

[invitebb1eae45]

Voila je pense que j'ai oublié le ² sur (Di+e)²

alors s est une formule qui viens du faite que pour la mesure ultrason en mode reflexe avec 2 transducteur sur le même plan on obtient un triangle rectangle qui nous permet d'appliquer pythagore et d'obtenir la longueur L

je sais pas si je suis un peu plus claire

[invitebb1eae45]

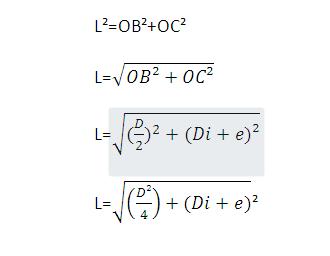
voila 2 schémas pour comprendre un peu mieux le sujet


SCHEMA Montage.JPG

schema montage 2.JPG

[Dlzlogic]

Bonjour,
Donc, vous avez une précision sur D, sur Di et sur e et vous voulez connaitre la précision sur L.
Que dit votre cours ? Je vous pose la question, parce que les avis sont partagés. En tout cas, ce que je vois est qu'il s'agit d'un vrai calcul dans le cadre d'une vraie situation.
Si je vous dis : "les incertitudes se combinent quadratiquement", vous réagissez comment ?

[invitebb1eae45]

bonjour ,

j'avoue que je ne sais pas trop quoi utilisé pour calculer mon incertitude mais ça pourrait etre plausible l'addition quadratique mais ça me parait trop simple ? Non?

[invitebb1eae45]

Apres dans la logique comme l'erreur est plus importante en faisant l'erreur quadratique je prendrai ce cas mais la j'avoue que je ne sais pas trop lequel prendre entre la somme quadratique et la derive de

[invitebd98b571]

Bonjour,

Dlzlogic a raison de vous demander les formules de votre cours. Il y a deux manières de calculer des incertitudes :

soit des incertitudes ponctuelles, par exemple ou ou , etc

soit des incertitudes statistiques, par exemple ou , etc

Ces deux manières de calculer les incertitudes ont leur contexte mathématique qui leur est propre, et il ne faut pas confondre les deux.
Quel est votre contexte ?

[gg0]

Bonjour.

Si tu veux faire le calcul d'incertitude sur cette nouvelle formule, tu appliques les même méthodes ...

Cordialement.

[invitebb1eae45]

je dois calculer l'incertitude sur L car pour ensuite voir l'impacte que cette incertitude peu avoir sur la vitesse calculer par un debitmetre a ultrason car L est la longue de parcours de l'onde voir schémas plus haut pour comprendre
Merci

[invitebd98b571]

vous avez un cours avec des formules ? quelles têtes ont-elles ? regardez les exemples que j'ai donnés et dites-nous lesquelles sont dans votre cours.

[invitebb1eae45]

Honnettement aucune formule que j'ai dans mon ressemble a ce que l'on viens de me donner a par la somme quadratique

[invitebd98b571]

vous dites que cette formule est dans votre cours ?

[gg0]

A priori, dans ce contexte, il ne s'agit pas de statistiques.

On appliquera alors les formules :

Qui s'écrit aussi
Et on interprètera la racine carrée comme une puissance 1/2.

Ces deux formules suffisent pour faire le calcul. Si on veut bien essayer de le faire.

[invitebd98b571]

Je suis d'accord, gg0, a priori le contexte est celui que vous précisez.
Mais les étudiants ont parfois du mal à préciser sur le forum le contexte de leur propre cours et ils oublient l'essentiel.
C'est déjà arriver plus d'une fois, et cela arrivera encore.
Est-ce le cas de seb6051 ?

[invitebb1eae45]

Je suis d'accord, gg0, a priori le contexte est celui que vous précisez.
Mais les étudiants ont parfois du mal à préciser sur le forum le contexte de leur propre cours et ils oublient l'essentiel.
C'est déjà arriver plus d'une fois, et cela arrivera encore.
Est-ce le cas de seb6051 ?

Bonjour,
non je n'ai aucune formule de ce type dans mon cours en revanche je suis tombé dessus sur un formulaire d'internet

Merci

[invitebb1eae45]

désolé je me suis tromper dans la formule de base

L = √((D²/4)+(Di+e)²)