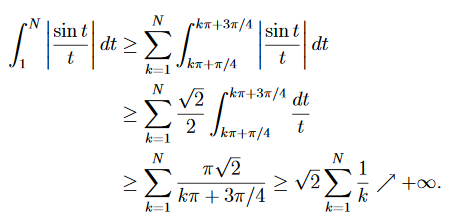Bonjour,
Je cherche à démontrer quediverge. J'y arrive en minorant le
Je ne vois pas du tout les arguments qui permettent de justifier les deux premières inégalités.
Pour la première je ne comprends pas les bornes et la deuxième je ne comprends pas comment le sinus disparait
Merci d'avance
Bonjour,
Pour la première, le terme sous l'intégrale étant positif, l'intégrale sur l'intervalle 0 à pi est toujours supérieure à celle sur un intervalle plus réduit, comme par exemple Pi/4, 3pi/4, de même pour l'intégrale entre kpi et (k+1)pi, supérieure à celle sur l'intervalle kpi+pi/4, kpi+3pi/4.
Quand on additionne ces inégalités, on trouve le résultat.
Ensuite, si on trace la courbe de |sin(t)| entre pi/4 et 3pi/4, on remarque que la courbe est toujours supérieure à |sin(pi/4)| soit racine(2)/2 et c'est vrai aussi pour les autres arches décalés de kpi.... donc les intégrales sont également supérieures.
Ensuite, comme racine(2)/2 est une constante, on peut la sortir des intégrales...
Why, sometimes I've believed as many as six impossible things before breakfast
Merci de votre réponse !
Pour la deuxième inégalité j'ai bien compris, cependant pour la première j'avais pensé à ça mais cela semble contredire l'inégalité puisque
L'amplitude est de
Il y a une erreur dans le démarrage de ta preuve, on calcule en fait
Sans doute un passage incomplet de
Cordialement.
Dernière modification par gg0 ; 10/09/2017 à 15h59.
